|
Постройте таблицу значений функции |
Реализация линейного и разветвляющегося алгоритмов
Занятие 2. Программная реализация разветвляющегося алгоритма
При рассмотрении разветвляющегося алгоритма будет разобран набор задач и примеров, которые являются усложненными версиями уже разобранных выше задач.
Будут приведены примеры вычисления функций, заданных на разных промежутках кусочно. Также приведены принцип и примеры расчетов для кусочных функций, заданных на двух промежутках и на трех промежутках.
Пример 5. Даны числа 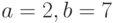 . Вычислить сумму
. Вычислить сумму  и разность
и разность  чисел
чисел  и
и  . Сравнить полученные значения
. Сравнить полученные значения  и
и  и указать большее из них.
и указать большее из них.
Блок-схема представлена на рис. 4.5.
Код программы (Visual Studio):
// proga14.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
using namespace std;
int main()
{
double a, b, S, R;
a=2;
b=7;
S=a+b;
R=a-b;
cout<<"S="<<S<<" R="<<R<<endl;
if(S>R) cout<<"Max S"<<endl;
else cout<<"Max R"<<endl;
return 0;
}Результат выполнения программы (Visual Studio):
Код программы (Borland C++):
#include <iostream.h>
int main(){
double a, b, S, R;
a=2;
b=7;
S=a+b;
R=a-b;
cout<<"S="<<S<<" R="<<R<<endl;
if(S>R) cout<<"Max S"<<endl;
else cout<<"Max R"<<endl;
return 0;
}Результат выполнения программы:
Пример 6. Составить блок-схему и программу для вычисления значений функций 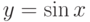 и
и 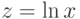 при различных значениях аргумента. Учесть область определения функций.
при различных значениях аргумента. Учесть область определения функций.
Решение. Рассмотрим области определения функций  и
и  . Синус имеет неограниченную область определения, т.е. считается при любом действительном
. Синус имеет неограниченную область определения, т.е. считается при любом действительном  . Поэтому на расчет функции y не будет никаких условий. Логарифм же существует при положительном значении аргумента, т.е. считается при
. Поэтому на расчет функции y не будет никаких условий. Логарифм же существует при положительном значении аргумента, т.е. считается при  . Поэтому, прежде чем считать функцию
. Поэтому, прежде чем считать функцию  , необходимо проверить условие "
, необходимо проверить условие " ". Если условие верно, то можно считать
". Если условие верно, то можно считать  . Если ложно, то
. Если ложно, то  считать нельзя, и в этом случае мы напишем в ответ, что
считать нельзя, и в этом случае мы напишем в ответ, что  не существует фразой "
не существует фразой " ".
".
Блок-схема представлена на рис. 4.6.
Код программы (Visual Studio):
// proga15.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <math.h>
using namespace std;
int main()
{
double x, y, z;
cout<<"vvedi x=";
cin>>x;
y=sin(x);
cout<<"y="<<y;
if(x>0){
z=log(x);
cout<<" z="<<z<<endl;
}
else cout<<" z net"<<endl;
return 0;
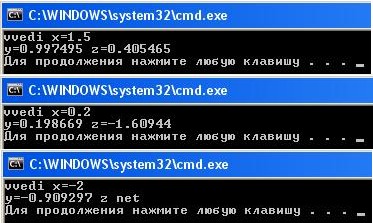
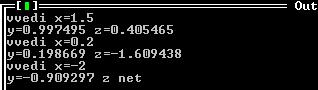
}Результат выполнения программы:
Код программы (Borland C++):
#include <iostream.h>
#include <math.h>
int main(){
double x, y, z;
cout<<"vvedi x=";
cin>>x;
y=sin(x);
cout<<"y="<<y;
if(x>0){
z=log(x);
cout<<" z="<<z<<endl;
}
else cout<<" z net"<<endl;
return 0;
}Результат выполнения программы:
Пример 7. Вычислить значение функции 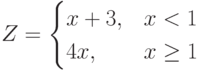 при различных значениях аргумента
при различных значениях аргумента  (аргумент
(аргумент  считать с клавиатуры).
считать с клавиатуры).
Решение: Функция  задана как кусочная функция, т.е. при разных значениях
задана как кусочная функция, т.е. при разных значениях  она считается по-разному. Следует отметить, что при одном значении аргумента функция будет иметь лишь одно значение, т.е. функция однозначная. График функции
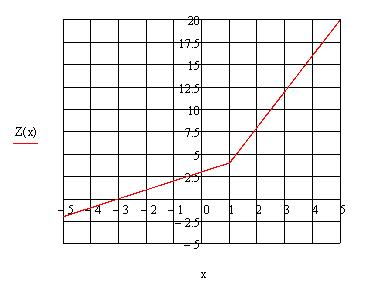
она считается по-разному. Следует отметить, что при одном значении аргумента функция будет иметь лишь одно значение, т.е. функция однозначная. График функции  представлен на рис. 4.7.
представлен на рис. 4.7.
Посчитаем значение функции  при
при  . Прежде всего необходимо проверить, какое условие верно: "
. Прежде всего необходимо проверить, какое условие верно: " " или "
" или " ". Условие для первой ветки функции верно, значит считаем
". Условие для первой ветки функции верно, значит считаем 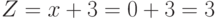 .
.
Посчитаем значение функции  при
при 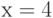 . Прежде всего необходимо проверить, какое условие верно: "
. Прежде всего необходимо проверить, какое условие верно: " " или "
" или " ". Условие для второй ветки функции верно, значит считаем
". Условие для второй ветки функции верно, значит считаем 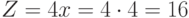 .
.
При расчете кусочной функции так или иначе сначала проводится проверка условия, поэтому вычисление таких функций реализуется через разветвляющийся алгоритм. В данном примере будет один блок разветвления (соответственно один оператор if в программе). Условием будет служить проверка " ". Если условие верно, то функция считается по первой ветке, если ложно, то по второй ветке. Второе условие "
". Если условие верно, то функция считается по первой ветке, если ложно, то по второй ветке. Второе условие " " будет лишним, т.к. оно соответствует стрелке "нет" от первого условия "
" будет лишним, т.к. оно соответствует стрелке "нет" от первого условия " ".
".
Примечание. Функция  – это функция, которая имеет один аргумент. Не следует путать запись кусочной функции с системой уравнений или системой неравенств, уравнения или неравенства которых также объединены фигурной скобкой. При расчете кусочной функции не решается никакая система уравнений, система неравенств, а просто подставляется конкретное значение аргумента и вычисляется значение функции.
– это функция, которая имеет один аргумент. Не следует путать запись кусочной функции с системой уравнений или системой неравенств, уравнения или неравенства которых также объединены фигурной скобкой. При расчете кусочной функции не решается никакая система уравнений, система неравенств, а просто подставляется конкретное значение аргумента и вычисляется значение функции.
Примечание. При расчете функции  не следует сразу рассчитывать обе ветки функции, т.к. в ответ нам нужен только один результат. Корректно составленный алгоритм не должен быть избыточен. Не следует повторять одно и то же по сути условие.
не следует сразу рассчитывать обе ветки функции, т.к. в ответ нам нужен только один результат. Корректно составленный алгоритм не должен быть избыточен. Не следует повторять одно и то же по сути условие.
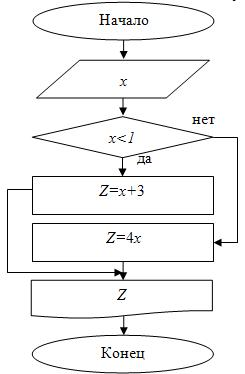
Блок-схема для примера 7 представлена на рис. 4.8.
Код программы (Visual Studio):
// proga16.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
using namespace std;
int main(){
double x, Z;
cout<<"x=";
cin>>x;
if(x<1){
Z=x+3;
}
else {
Z=4*x;
}
cout<<"Z="<<Z<<endl;
return 0;
}Результат выполнения программы:
Код программы (Borland C++):
#include <iostream.h>
int main(){
double x, Z;
cout<<"x=";
cin>>x;
if(x<1){
Z=x+3;
}
else { Z=4*x;
}
cout<<"Z="<<Z<<endl;
return 0;
}Результат выполнения программы:
Пример 8. Вычислить значение функции 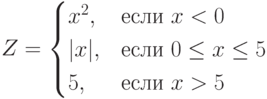 при различных значениях аргумента
при различных значениях аргумента  (аргумент
(аргумент  считать с клавиатуры).
считать с клавиатуры).
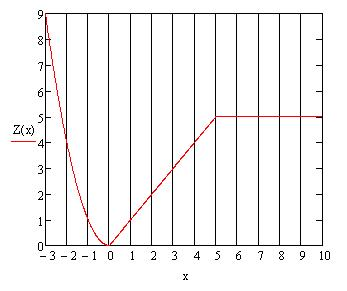
Решение: Функция  задана как кусочная функция, определенная на трех промежутках. График функции
задана как кусочная функция, определенная на трех промежутках. График функции  представлен на рис. 4.9.
представлен на рис. 4.9.
В данной задаче будем использовать два условия для определения нужной ветви функции. Первое условие " " определяет, следует ли рассчитывать по первой ветви функции. Второе условие "
" определяет, следует ли рассчитывать по первой ветви функции. Второе условие " " определяет, следует ли рассчитывать по второй ветви. Если и первое, и второе условия оказались ложными (не выполнились), то следует рассчитывать по третьей ветви. Следовательно, в блок-схеме будем использовать два блока разветвления, а в программе два оператора условия if.
" определяет, следует ли рассчитывать по второй ветви. Если и первое, и второе условия оказались ложными (не выполнились), то следует рассчитывать по третьей ветви. Следовательно, в блок-схеме будем использовать два блока разветвления, а в программе два оператора условия if.
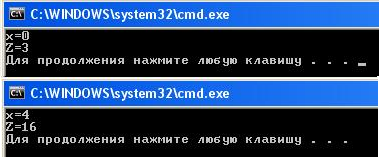
Например, нужно вычислить  при
при 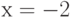 . Первое условие "
. Первое условие " " выполняется верно, т.к.
" выполняется верно, т.к. 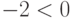 . Следовательно, считать следует по первой ветви, а именно:
. Следовательно, считать следует по первой ветви, а именно: 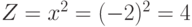 .
.
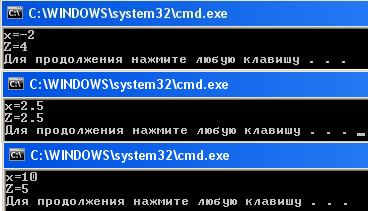
Например, нужно вычислить  при
при 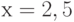 . Первое условие "
. Первое условие " " выполняется неверно, т.к. 2,5>0. Проверяем второе условие "
" выполняется неверно, т.к. 2,5>0. Проверяем второе условие " ": 2,5≤5 – верно. Следовательно, считать следует по второй ветви, а именно:
": 2,5≤5 – верно. Следовательно, считать следует по второй ветви, а именно:  .
.
Например, нужно вычислить  при
при 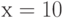 . Первое условие "
. Первое условие " " выполняется неверно, т.к. 10>0. Проверяем второе условие "
" выполняется неверно, т.к. 10>0. Проверяем второе условие " ": 10≤5 – неверно. Следовательно, ни первое, ни второе условия не выполнились, и считать следует по третьей ветви, а именно:
": 10≤5 – неверно. Следовательно, ни первое, ни второе условия не выполнились, и считать следует по третьей ветви, а именно: 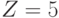 .
.
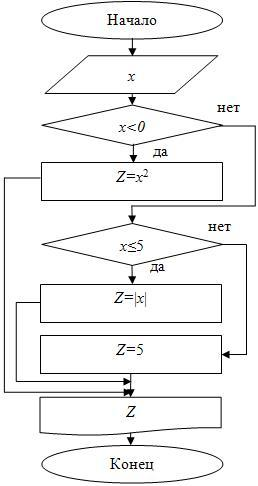
Блок-схема представлена на рис. 4.10.
Код программы (Visual Studio):
// proga17.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <math.h>
using namespace std;
int main(){
double x,Z;
cout<<"x=";
cin>>x;
if(x<0){ Z=pow(x, 2.0);
}
else {if(x<=5){
Z=fabs(x);}
else {
Z=5.0;}
}
cout<<"Z="<<Z<<endl;
return 0;
}Результат выполнения программы (Visual Studio):
Код программы (Borland C++):
#include <iostream.h>
#include <math.h>
int main(){
double x, Z;
cout<<"x=";
cin>>x;
if(x<0){
Z=pow(x, 2.0);
}
else {
if(x<=5){
Z=fabs(x);
}
else {
Z=5.0;
}
}
cout<<"Z="<<Z<<endl;
return 0;
}Результат выполнения программы (Borland C++):
Примечание. В качестве второго условия можно, конечно, взять "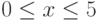 ". Но при проверке первого условия мы уже знаем, будет ли
". Но при проверке первого условия мы уже знаем, будет ли  . Поэтому можно пропустить повторную проверку на положительность переменной
. Поэтому можно пропустить повторную проверку на положительность переменной  . Также в качестве второго условия можно взять условие "
. Также в качестве второго условия можно взять условие " ". Если оно выполнится верно, то считать следует по третьей ветви, если неверно – то по второй.
". Если оно выполнится верно, то считать следует по третьей ветви, если неверно – то по второй.
Пример 9. Вычислить значение функции 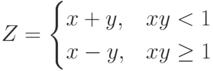 при различных значениях аргументов
при различных значениях аргументов  и
и  (аргументы
(аргументы  и
и  считать с клавиатуры).
считать с клавиатуры).
Решение: Данный Пример аналогичен Примеру 7. Отличие состоит в том, что сейчас функция  зависит от двух переменных
зависит от двух переменных  и
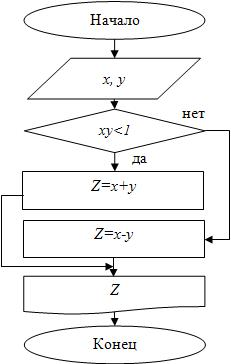
и  . Для реализации алгоритма разницы нет, поэтому за основу возьмем блок-схему и программу из Примера 7.
. Для реализации алгоритма разницы нет, поэтому за основу возьмем блок-схему и программу из Примера 7.
Блок-схема представлена на рис. 4.11.
Код программы (Visual Studio):
// proga18.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
using namespace std;
int main(){
double x, y, Z;
cout<<"x=";
cin>>x;
cout<<"y=";
cin>>y;
if(x*y<1){ Z=x+y;
}
else {Z=x-y;
}
cout<<"Z="<<Z<<endl;
return 0;}Результат выполнения программы (Visual Studio):
Код программы (Borland C++):
#include <iostream.h>
int main(){
double x, y, Z;
cout<<"x=";
cin>>x;
cout<<"y=";
cin>>y;
if(x*y<1){
Z=x+y;
}
else {
Z=x-y;
}
cout<<"Z="<<Z<<endl;
return 0;
}Результат выполнения программы (Borland C++):
Ручной счет.
при х=-3; у=0,5 ху=-3·0,5=-1,5 <1 Z=x+y=-3+0,5=-2,5. при x=0,8; y=2 xy=0,8·2=1,6≥1 Z=x-y=0,8-2=-1,2.
Пример 10. Вычислить значение функции 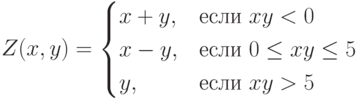 при различных значениях аргументов
при различных значениях аргументов  и
и  (аргументы
(аргументы  и
и  считать с клавиатуры).
считать с клавиатуры).
Решение. В данном примере функция  определена на трех промежутках, как в Примере 8. Отличие состоит в том, что
определена на трех промежутках, как в Примере 8. Отличие состоит в том, что  зависит от двух переменных
зависит от двух переменных  и
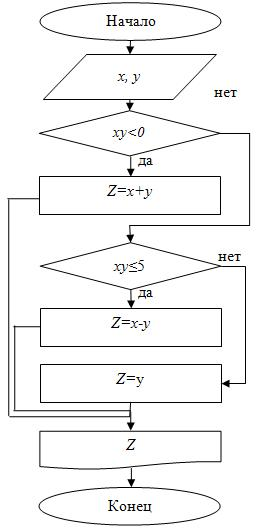
и  . Для реализации алгоритма разницы нет, поэтому за основу возьмем блок-схему и программу из Примера 8.
. Для реализации алгоритма разницы нет, поэтому за основу возьмем блок-схему и программу из Примера 8.
Блок-схема представлена на рис. 4.12.
Код программы (Visual Studio):
// proga19.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
using namespace std;
int main(){
double x, y, Z;
cout<<"x=";
cin>>x;
cout<<"y=";
cin>>y;
if(x*y<0){ Z=x+y;}
else {
if(x*y<=5){
Z=x-y;
}
else {
Z=y;
}
}
cout<<"Z="<<Z<<endl;
return 0;
}Результат выполнения программы (Visual Studio):
Код программы (Borland C++):
#include <iostream.h>
int main(){
double x, y, Z;
cout<<"x=";
cin>>x;
cout<<"y=";
cin>>y;
if(x*y<0){
Z=x+y;
}
else {
if(x*y<=5){
Z=x-y;
}
else {
Z=y;
}
}
cout<<"Z="<<Z<<endl;
return 0;
}Результат выполнения программы (Borland C++):
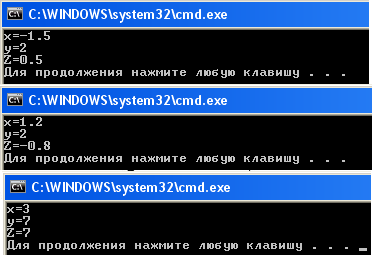
Ручной счет:
при х=-1,5; у=2 ху=-1,5·2=-3 <0 Z={по первой ветви}=x+y=-1,5+2=0,5.
при x=1,2; y=2 xy=1,2·2=2,4≤5 Z={по второй ветви}=x-y=1,2-2=-0,8.
при x=3; y=7 xy=3·7=21 >5 Z={по третьей ветви}=y=7.Пример 11. Найти наибольшее (максимальное) из трех чисел.
Решение. Обозначим три числа буквами 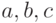 . Числа
. Числа 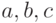 будем считывать с клавиатуры. Для нахождения наибольшего из трех чисел введем еще одну переменную
будем считывать с клавиатуры. Для нахождения наибольшего из трех чисел введем еще одну переменную 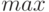 , которая будет хранить наибольшее значение. Принцип нахождения наибольшего значения заключается в следующем. Сначала принимаем
, которая будет хранить наибольшее значение. Принцип нахождения наибольшего значения заключается в следующем. Сначала принимаем 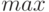 как первое число
как первое число  . Потом поочередно сравниваем с оставшимися числами
. Потом поочередно сравниваем с оставшимися числами  и
и  . Если окажется, что
. Если окажется, что  больше уже запомненного
больше уже запомненного 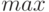 , то следует перезаписать
, то следует перезаписать 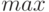 , изменив его значение на значение
, изменив его значение на значение  . Если же
. Если же  , то
, то 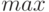 изменять не нужно, поэтому ветвь "нет" будет пустой. Аналогично сравниваем
изменять не нужно, поэтому ветвь "нет" будет пустой. Аналогично сравниваем  и
и 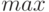 . После двух сравнений в переменной
. После двух сравнений в переменной 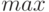 будет лежать наибольшее из трех чисел.
будет лежать наибольшее из трех чисел.
Примечание. Если чисел будет больше трех, например, пять чисел, то следует сделать четыре сравнения.
Примечание. Если нужно определить наименьшее из трех чисел, то вводят переменную 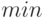 , приравнивают к первому числу. Затем поочередно сравнивают оставшиеся числа: "
, приравнивают к первому числу. Затем поочередно сравнивают оставшиеся числа: "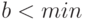 ", "
", "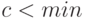 ".
".
Если нужно определить наименьшее из большего числа чисел, например, из пяти чисел, то следует сделать четыре сравнения.
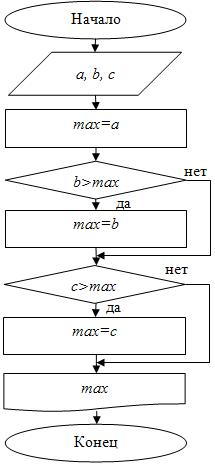
Блок-схема представлена на рис. 4.13.
Выполнение блок-схемы (при вводимых значениях чисел 23,7; -0,4; 34,28)
Начало ввод данных a=23,7; b=-0,4; c=34,28
max=a=23,7 b>max -0,4>23,7 нет c>max 34,28>23,7 да max=c=34,28 вывод max
Конец.
Код программы (Visual Studio):
// proga20.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
using namespace std;
int main()
{
double a, b, c, max;
cout<<"a=";
cin>>a;
cout<<"b=";
cin>>b;
cout<<"c=";
cin>>c;
max=a;
if(b>max){
max=b;
}
if(c>max){
max=c;
}
cout<<"max="<<max<<endl;
return 0;
}Результат выполнения программы (Visual Studio):
Код программы (Borland C++):
#include <iostream.h>
int main(){
double a, b, c, max;
cout<<"a=";
cin>>a;
cout<<"b=";
cin>>b;
cout<<"c=";
cin>>c;
max=a;
if(b>max){
max=b;
}
if(c>max){
max=c;
}
cout<<"max="<<max<<endl;
return 0;
}Результат выполнения программы (Borland C++):
Пример 12. Найти значение функции 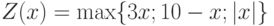 при различных значениях аргумента
при различных значениях аргумента  (аргумент
(аргумент  считать с клавиатуры).
считать с клавиатуры).
Решение. Функция  считается как наибольшее из трех выражений. Задача схожа с Примером 11. Введем обозначения:
считается как наибольшее из трех выражений. Задача схожа с Примером 11. Введем обозначения: 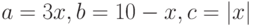 . Тогда наша задача максимально будет похожа на Пример 11.
. Тогда наша задача максимально будет похожа на Пример 11.
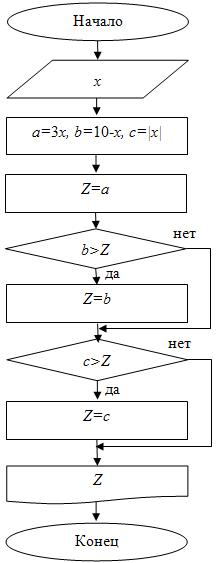
Блок-схема представлена на рис. 4.14.
Выполнение блок-схемы (при вводимом x=1)
Начало ввод x=1
a=3x=3·1=3 b=10-x=10-1=9 c=|x|=|1|=1 Z=a=3 b>Z 9>3 да Z=b=9 c>Z 1>9 нет вывод Z
Конец.
Код программы (Visual Studio):
// proga21.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <math.h>
using namespace std;
int main(){
double x, a, b, c, Z;
cout<<"x=";
cin>>x;
a=3.0*x;
b=10.0-x;
c=fabs(x);
Z=a;
if(b>Z){Z=b;}
if(c>Z){Z=c;}
cout<<"Z="<<Z<<endl;
return 0;
}Результат выполнения программы (Visual Studio):
Код программы (Borland C++):
#include <iostream.h>
#include <math.h>
int main(){
double x, a, b, c, Z;
cout<<"x=";
cin>>x;
a=3.0*x;
b=10.0-x;
c=fabs(x);
Z=a;
if(b>Z){
Z=b;
}
if(c>Z){
Z=c;
}
cout<<"Z="<<Z<<endl;
return 0;
}Результат выполнения программы (Borland C++):
Пример 13. Найти значение функции, заданной по формуле 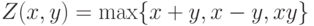 при различных значениях аргументов
при различных значениях аргументов  и
и  (аргументы
(аргументы  и
и  считать с клавиатуры).
считать с клавиатуры).
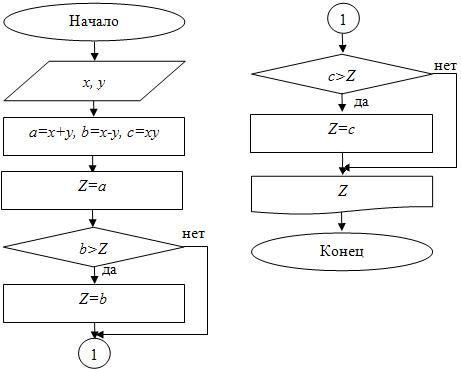
Блок-схема представлена на рис. 4.15.
Код программы (Visual Studio):
// proga22.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
using namespace std;
int main()
{
double x, y, a, b, c, Z;
cout<<"x=";
cin>>x;
cout<<"y=";
cin>>y;
a=x+y;
b=x-y;
c=x*y;
Z=a;
if(b>Z){
Z=b;
}
if(c>Z){
Z=c;
}
cout<<"Z="<<Z<<endl;
return 0;
}Результат выполнения программы (Visual Studio):
Код программы (Borland C++):
#include <iostream.h>
int main(){
double x, y, a, b, c, Z;
cout<<"x=";
cin>>x;
cout<<"y=";
cin>>y;
a=x+y;
b=x-y;
c=x*y;
Z=a;
if(b>Z){
Z=b;
}
if(c>Z){
Z=c;
}
cout<<"Z="<<Z<<endl;
return 0;
}Результат выполнения программы (Borland C++):
Краткие итоги
Одна и та же блок-схема может быть использована при написании разных программ С++. Результат выполнения программы из-за этого не должен меняться.
Упражнения
- Составьте блок-схему и программу для вычисления значений функций
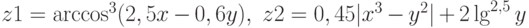 при различных значениях аргументов
при различных значениях аргументов  и
и  .
. - Составьте блок-схему и программу по нахождению корней квадратного уравнения через дискриминант. Коэффициенты квадратного уравнения считывайте с клавиатуры.
- Составьте блок-схему и программу, которая спрашивает у пользователя возраст и в соответствии с возрастной группой ("дошкольник", "школьник", "взрослый", "пожилой") выдает соответствующую фразу на экран.
- Составьте блок-схему и программу для вычисления значения функции
![Z(x,y)=\begin{cases}\sin^{0.4}(4^{4y})+\lg\sqrt{y-\frac{x}{y-0.8}},&\text{если}\ x+y<-2\\2.3,&\text{если}\ -2\le x+y\le 0\\\frac{\sqrt[3]{x}-\sqrt[3]{y}}{x}-y,&\text{если}\ x+y>0\end{cases}](/sites/default/files/tex_cache/8bdc9377e050f7d958705bd07d8bc06a.png) при разных значениях аргументов
при разных значениях аргументов  и
и  .
. - Составьте блок-схему и программу для вычисления значений функции
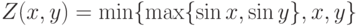 при разных значениях аргументов
при разных значениях аргументов  и
и  .
.


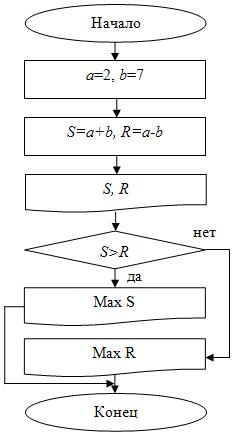


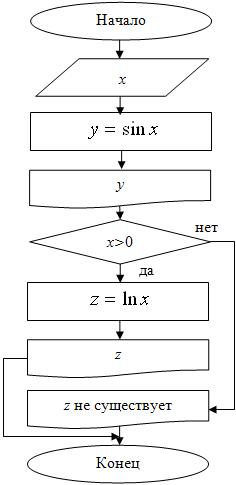








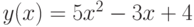 при
при 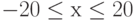 с шагом 0,5. Определите наименьшее значение функции и значение
с шагом 0,5. Определите наименьшее значение функции и значение  , при котором оно достигается.
, при котором оно достигается.