Лекция 6: Нормальные формы отношений. Создание логической модели реляционной базы данных

Пятая нормальная форма

Как можно заметить, нормализация отношений выполнялась путем разложения (декомпозиции) схем отношений. Очевидно, что при таком подходе должен соблюдаться принцип обратимости: соединение проекций должно приводить к исходным отношениям. Это предполагает отсутствие потери кортежей; появление ранее не существовавших кортежей; сохранение ФЗ (семантика взаимосвязей между данными не должна нарушаться).

Декомпозиция схем отношений не всегда гарантирует обратимость. Это обстоятельство связано с существованием класса ФЗ по соединению. Если отношение удовлетворяет ФЗ по соединению, то оно может быть восстановлено по своим проекциям. Отношения, содержащие более трех МФЗ, требуют особого внимания при построении логической модели реляционной базы данных. Также 4НФ не устраняет избыточность данных полностью, поэтому требуется дальнейшая декомпозиция схем отношений.

Отношение находится в пятой нормальной форме (5НФ), если оно находится в 4НФ и удовлетворяет зависимости по соединению относительно своих проекций. 5НФ называют также нормальной формой с проецированием соединений. Она используется для разрешения трех и более отношений, которые связаны более чем тремя ФЗ по типу "многие-ко-многим".

Пример. Приведение к 5НФ

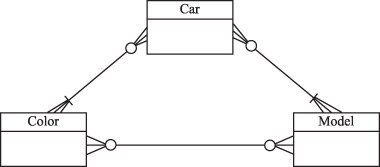
Рассмотрим отношение с несколькими многозначными зависимостями, представленное на рис. 6.8.

Рис. 6.8. Отношение с несколькими многозначными зависимостями

Рассмотрим сначала это отношение как три изолированных отношения со степенью связи quot;многие-ко-многимquot;:

Каждый автомобиль имеет определенный цвет и модель. Некоторые цвета характерны только для определенных моделей. Такие отношения разрешаются введением связывающих отношений, в данном случае таких отношений три:

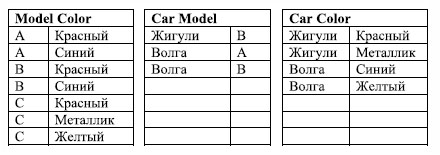
Предположим, что клиент желает приобрести автомобиль синего цвета модели С, при этом марка автомобиля роли не играет. Запрос к базе данных на поиск такого автомобиля будет содержать два соединения между тремя таблицами Car, Car Color и Car Model по атрибуту наименование машины и два предиката: цвет = синий и модель = С.

Результат выполнения запроса будет удивителен: есть и Волга, и Жигули! Однако из таблицы Model Color видно, что автомобиля синего цвета модели С не существует. Появляется несуществующий кортеж. Такое явление представляет собой аномалию проецирования соединений и пример нарушения 5НФ.

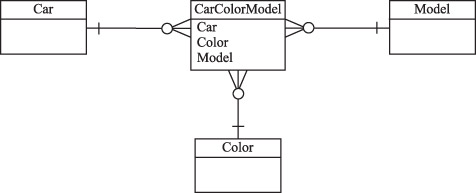
Приведение отношения к 5НФ заключается во введении еще одного отношения, связывающего три исходных отношения, как показано на рис. 6.9.

Рис. 6.9. Отношение в 5НФ

Таким образом, процедура приведения отношения, содержащего многозначные ФЗ, к 5НФ состоит в построении связывающего отношения, позволяющего исключить появление в соединениях ложных кортежей.

Следовательно, каждая нормальная форма ограничивает определенный тип ФЗ и устраняет аномалии обработки данных. Нормальные формы характеризуются следующими свойствами:

• 1НФ - все атрибуты отношения простые;
• 2НФ - отношение находится в 1НФ и не содержит частичных ФЗ;
• 3НФ - отношение находится во 2НФ и не содержит транзитивных ФЗ от ключа;
• НФБК - отношение находится в 3НФ и не содержит ФЗ ключей от неключевых атрибутов;
• 4НФ, применяется при наличии более чем одной многозначной ФЗ - отношение находится в НФБК или 3НФ и не содержит независимых многозначных ФЗ;
• 5НФ - отношение находится в 4НФ и не содержит ФЗ по соединению.

Литература: [2], [3], [15], [14], [16], [20], [31], [37], [39], [43], [44], [45].