Индуктивные функции на пространстве последовательностей
Критерий минимальности
Перед тем, как сформулировать критерий минимальности, докажем существование минимального индуктивного расширения.
Теорема 9.3.
Минимальное индуктивное расширение для любой функции 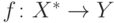 существует.
существует.
Доказательство
Для доказательства теоремы построим в три этапа каноническое
минимальное индуктивное расширение 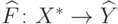 заданной функции
заданной функции  .
.
Первый этап.
Рассмотрим на множестве цепочек  бинарное отношение
бинарное отношение  ,
задаваемое формулой
,
задаваемое формулой 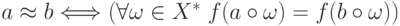 , и покажем, что
, и покажем, что
1)  — отношение эквивалентности на
— отношение эквивалентности на  ;
;
2)  ;
;
3)  .
.
Рефлексивность, симметричность и транзитивность отношения  вытекают
соответственно из рефлексивности, симметричности и транзитивности отношения
равенства.
вытекают
соответственно из рефлексивности, симметричности и транзитивности отношения
равенства.
Так как 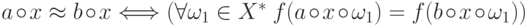 , то взяв в
качестве
цепочки
, то взяв в
качестве
цепочки 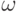 , фигурирующей в определении отношения
, фигурирующей в определении отношения  ,
,  , убеждаемся в истинности второго
свойства.
, убеждаемся в истинности второго
свойства.
Свойство 3) немедленно следует из определения отношения  , если в
качестве
, если в
качестве 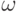 взять пустую цепочку
взять пустую цепочку 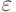 .
.
Второй этап.
Построим пространство 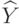 и отображение
и отображение 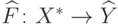 .
В качестве
.
В качестве 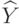 возьмем фактормножество (множество классов
эквивалентности)
возьмем фактормножество (множество классов
эквивалентности) 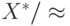 , что можно сделать в силу свойства
1).
Договоримся обозначать класс эквивалентности,
содержащий цепочку
, что можно сделать в силу свойства
1).
Договоримся обозначать класс эквивалентности,
содержащий цепочку 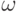 через
через ![[\omega]](/sites/default/files/tex_cache/da896e39037cfacf15c231efe98a05e6.png) и определим
отображение
и определим
отображение 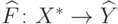 формулой
формулой ![\widehat F(\omega)=
[\omega]](/sites/default/files/tex_cache/4a57f44876f53121ca19a08b808d386d.png) .
.
Переписав свойство 2) в эквивалентном виде 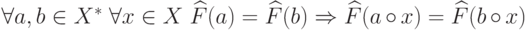 , из критерия
индуктивности заключаем, что отображение
, из критерия
индуктивности заключаем, что отображение  —
индуктивно.
—
индуктивно.
Покажем, что  является индуктивным расширением
исходной функции
является индуктивным расширением
исходной функции 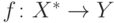 . Определим проекцию
. Определим проекцию 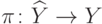 формулой
формулой ![\pi([\omega])=f(\omega)](/sites/default/files/tex_cache/d5c1585f54eec498c55f7bea48824a81.png) .
Корректность этого
определения следует из свойства 3) — если две цепочки
.
Корректность этого
определения следует из свойства 3) — если две цепочки 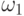 и
и 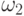 принадлежат одному классу эквивалентности, то значение
функции
принадлежат одному классу эквивалентности, то значение
функции  на них совпадает. Так как
на них совпадает. Так как  для
произвольной цепочки
для
произвольной цепочки  , то
, то  действительно является
индуктивным расширением отображения
действительно является
индуктивным расширением отображения  .
.
Третий этап. Нам осталось показать, что построенное каноническое индуктивное расширение является минимальным.
Сюръективность  следует непосредственно из его
построения, ибо
каждый класс эквивалентности
следует непосредственно из его
построения, ибо
каждый класс эквивалентности ![[\omega]](/sites/default/files/tex_cache/da896e39037cfacf15c231efe98a05e6.png) не пуст.
не пуст.
Предположим далее, что существует 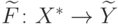 — иное индуктивное расширение
исходной функции
— иное индуктивное расширение
исходной функции  , тогда для завершения
доказательства теоремы нам необходимо показать, что
, тогда для завершения
доказательства теоремы нам необходимо показать, что 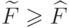 .
.
Определим проекцию 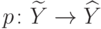 формулой
формулой ![p(y) = [\omega]](/sites/default/files/tex_cache/014fb5cb3ab2955044633279324bfd0b.png) , где
, где 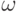 — один из прообразов
элемента
— один из прообразов
элемента 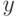 при
отображении
при
отображении 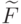 . Проверим корректность данного
определения.
. Проверим корректность данного
определения.
Пусть 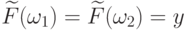 .
Тогда в силу
индуктивности
.
Тогда в силу
индуктивности 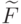 для произвольной цепочки
для произвольной цепочки 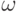 справедливо
равенство
справедливо
равенство  , а так как
, а так как 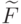 —
индуктивное расширение
функции
—
индуктивное расширение
функции  , то и
, то и  .
Полученное равенство может быть переписано в виде
.
Полученное равенство может быть переписано в виде ![[\omega_1]=[\omega_2]](/sites/default/files/tex_cache/42ae1401bf43a5db4857d0a4e5bc2731.png) ,
показывающем корректность определения проекции
,
показывающем корректность определения проекции 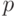 .
.
Равенство ![\widehat F(\omega) = [\omega] = p(\widetilde
F(\omega))](/sites/default/files/tex_cache/adbeef39b57571f79ade3bcb562a3822.png) для
произвольной цепочки
для
произвольной цепочки  показывает, что
показывает, что 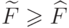 . Теорема полностью доказана.
. Теорема полностью доказана.
Построенное в процессе доказательства этой теоремы каноническое индуктивное расширение позволяет убедиться в истинности следующего критерия минимальности.
Теорема 9.4. Критерий минимальности. Индуктивное расширение 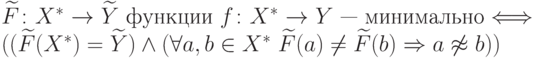 .
.
Доказательство
Необходимость первого условия критерия следует непосредственно из определения
минимальности. Второе условие выполнено по построению для канонического
минимального индуктивного расширения 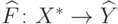 , а так как по теореме
единственности отображения
, а так как по теореме
единственности отображения  и
и 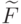 изоморфны, то и для
изоморфны, то и для 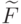 .
.
Для доказательства достаточности рассмотрим
каноническое минимальное индуктивное расширение 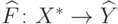 и покажем, что оно
изоморфно
нашему
и покажем, что оно
изоморфно
нашему  .
В силу минимальности
.
В силу минимальности  существует отображение
существует отображение 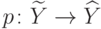 , такое что
, такое что 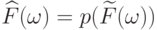 для произвольной
цепочки
для произвольной
цепочки  . Критерий будет доказан, если мы покажем,
что
отображение
. Критерий будет доказан, если мы покажем,
что
отображение 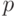 — биекция.
— биекция.
Сюръективность 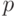 вытекает из сюръективности
вытекает из сюръективности 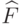 и
и 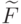 ,
а инъективность доказывается следующим рассуждением.
Рассмотрим различные
,
а инъективность доказывается следующим рассуждением.
Рассмотрим различные  и
и 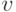 из
из  и,
воспользовавшись сюръективностью
и,
воспользовавшись сюръективностью 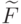 , найдем цепочки
, найдем цепочки 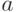 и
и 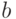 из
из  такие, что
такие, что 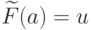 , а
, а 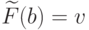 .
Так как
.
Так как  , то в силу данного нам
условия
, то в силу данного нам
условия  , что эквивалентно неравенству
, что эквивалентно неравенству 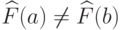 .
.
Следовательно, отображение 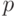 различные
различные  и
и 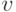 преобразует в различные
же
преобразует в различные
же  и
и  , что и
требовалось доказать.
, что и
требовалось доказать.
Докажем, что функция  ,
определенная
по формуле
,
определенная
по формуле 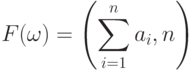 , где
, где 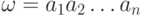 ,
,  и
и 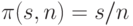 ,
является минимальным индуктивным расширением для
,
является минимальным индуктивным расширением для 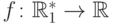 среднее арифметическое элементов последовательности. Для доказательства
сюръективности функции
среднее арифметическое элементов последовательности. Для доказательства
сюръективности функции 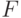 предъявим прообраз произвольного
элемента
предъявим прообраз произвольного
элемента  . Им будет цепочка из
. Им будет цепочка из 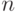 элементов, первый
из которых равен
элементов, первый
из которых равен  , а остальные — нулевые. Для того чтобы
проверить
второе условие критерия минимальности, необходимо убедиться в том, что
, а остальные — нулевые. Для того чтобы
проверить
второе условие критерия минимальности, необходимо убедиться в том, что  . Пусть
. Пусть 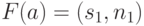 ,
,  и
либо
и
либо 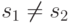 , либо
, либо  . Если для пустой
цепочки
. Если для пустой
цепочки 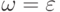 верно, что
верно, что  , то все
доказано. Иначе имеем
, то все
доказано. Иначе имеем  . Возьмем
теперь в
качестве
. Возьмем
теперь в
качестве 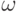 одноэлементную цепочку
одноэлементную цепочку  . Предположив, что
для нее
. Предположив, что
для нее  , из системы
, из системы

получим  ,
,  , что противоречит
предположению.
Это завершает доказательство минимальности
, что противоречит
предположению.
Это завершает доказательство минимальности 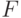 .
.
Минимальные индуктивные расширения обладают тем достоинством, что позволяют свести к минимуму ту дополнительную информацию, которая необходима для индуктивного перевычисления исходной функции. Иначе это свойство может быть сформулировано следующим образом.
Теорема 9.5.
Для произвольной функции  на пространстве последовательностей
существует единственный с точностью до изоморфизма однопроходный
алгоритм с минимальной емкостной сложностью.
на пространстве последовательностей
существует единственный с точностью до изоморфизма однопроходный
алгоритм с минимальной емкостной сложностью.
