Особенности представления чисел в ЭВМ
Вещественные числа
Обсуждаемые в данной секции вопросы значительно более полно рассмотрены в четвертой главе классической книги Кнута [7].
Для представления вещественных чисел в языке Java используют переменные и константы типов float и double. Величины первого из них занимают четыре байта, а второго — восемь.
В отличие от множества целых чисел 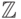 вещественные
числа
вещественные
числа  обладают свойством полноты: между любыми двумя
различными
числами всегда найдется отличное от них третье. Понятно, что любой из
способов представления бесконечного множества вещественных чисел с помощью
некоторого конечного множества
обладают свойством полноты: между любыми двумя
различными
числами всегда найдется отличное от них третье. Понятно, что любой из
способов представления бесконечного множества вещественных чисел с помощью
некоторого конечного множества  не даст возможности
сохранить
свойство полноты. Наиболее распространенным способом реализации вещественных
чисел на ЭВМ является использование чисел с плавающей точкой.
При этом множество
не даст возможности
сохранить
свойство полноты. Наиболее распространенным способом реализации вещественных
чисел на ЭВМ является использование чисел с плавающей точкой.
При этом множество  оказывается состоящим из
элементов вида
оказывается состоящим из
элементов вида

где целые числа 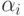 для всех
для всех  из диапазона от
1 до
из диапазона от
1 до  удовлетворяют
соотношению
удовлетворяют
соотношению  , а величина
, а величина  лежит
в диапазоне от
лежит
в диапазоне от  до
до  (
(  ). Число
). Число  является при этом основанием системы счисления (чаще всего это 2), константа
является при этом основанием системы счисления (чаще всего это 2), константа  задает точность представления чисел (для типа double она
больше,
чем для float ), а диапазон
задает точность представления чисел (для типа double она
больше,
чем для float ), а диапазон ![[L,U]](/sites/default/files/tex_cache/88a58043dcd0420a0c40020d0c799434.png) определяет область
значений
экспоненты (для типа double он также больше, чем для float ).
определяет область
значений
экспоненты (для типа double он также больше, чем для float ).
Число 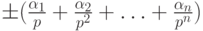 принято называть мантиссой числа
принято называть мантиссой числа  с
плавающей
точкой. Часто требуют, чтобы для всех чисел
с
плавающей
точкой. Часто требуют, чтобы для всех чисел 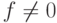 величина
величина 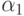 была ненулевой. Такие числа с плавающей точкой называют нормализованными.
была ненулевой. Такие числа с плавающей точкой называют нормализованными.
В языке Java для кодирования величин типов float и double
также используют числа с плавающей точкой. При этом часть из имеющегося
множества бит используют для размещения экспоненты  , а
остальные
биты — для размещения мантиссы.
, а
остальные
биты — для размещения мантиссы.
Для того чтобы хорошо понять, что же представляет из себя множество  нормализованных чисел с плавающей точкой, полезно
изобразить
его на числовой прямой для случая небольших
нормализованных чисел с плавающей точкой, полезно
изобразить
его на числовой прямой для случая небольших  ,
,  и
и  . Подобная задача
приведена в конце параграфа. Сейчас же нам будет достаточно весьма
качественного описания этого множества.
. Подобная задача
приведена в конце параграфа. Сейчас же нам будет достаточно весьма
качественного описания этого множества.
Так как  симметрично относительно начала
координат, то можно
разобраться только с неотрицательными числами. Нуль, конечно же, принадлежит
искомому множеству. Ближайшая к нулю следующая точка получается при
симметрично относительно начала
координат, то можно
разобраться только с неотрицательными числами. Нуль, конечно же, принадлежит
искомому множеству. Ближайшая к нулю следующая точка получается при 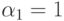 ,
,  и
и 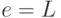 .
Это число для чисел
типов float
и double определено, как MIN_VALUE в классах java.lang.Float и java.lang.Double соответственно.
.
Это число для чисел
типов float
и double определено, как MIN_VALUE в классах java.lang.Float и java.lang.Double соответственно.
Правее располагается множество точек, следующих друг за другом с шагом  . Затем шаг
увеличивается. Потом еще. И еще. При
. Затем шаг
увеличивается. Потом еще. И еще. При 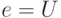 расстояние между двумя
соседними
точками множества
расстояние между двумя
соседними
точками множества  достигает
достигает 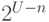 .
Самая правая точка
множества получается при
.
Самая правая точка
множества получается при  и
и 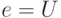 . Для типов float и double это число определено, как MAX_VALUE
в классах java.lang.Float и java.lang.Double.
. Для типов float и double это число определено, как MAX_VALUE
в классах java.lang.Float и java.lang.Double.
Кроме перечисленных (и симметричных им отрицательных) значений в результате выполнения некоторых операций могут получиться также следующие особые значения: плюс бесконечность ( POSITIVE\_INFINITY ), минус бесконечность ( NEGATIVE\_INFINITY ), минус ноль и не число ( NaN ). Например, при делении единицы на минус ноль получается минус бесконечность.
Описанные особенности множества машинных вещественных чисел  приводят к тому, что не для всех его элементов верны следующие соотношения,
всегда справедливые для множества настоящих вещественных чисел
приводят к тому, что не для всех его элементов верны следующие соотношения,
всегда справедливые для множества настоящих вещественных чисел  :
:
-
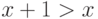 ;
; -
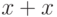 существует;
существует; -
 ;
; -
 ;
; -
 ;
; -
 .
.
Приведем несколько примеров, иллюстрирующих эти особенности множества  .
.
Задача 4.1. Предъявите действительное (типа double ) число  такое, что
такое, что 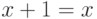 , а
, а  . Воспользуйтесь тем, что класс java.lang.Double определяет константу MAX_VALUE.
. Воспользуйтесь тем, что класс java.lang.Double определяет константу MAX_VALUE.
Текст программы
public class DblMaxVal {
public static void main(String[] args) {
double x = Double.MAX_VALUE;
double y = x + 1.0;
if (x == y) {
Xterm.print("Для числа ");
Xterm.print("x = " + x, Xterm.Blue);
Xterm.print(" величины x и (x+1) ");
Xterm.print("равны!\n", Xterm.Red);
}
y = 2.0 * x;
double z = y / 2.0;
if (x != z) {
Xterm.print("Для числа ");
Xterm.print("x = " + x, Xterm.Blue);
Xterm.print(" величины x и (2.0*x)/2.0 ");
Xterm.print("различны\n", Xterm.Red);
Xterm.print("и равны соответственно");
Xterm.print(" " + x, Xterm.Red);
Xterm.print(" и");
Xterm.print(" " + z + "\n", Xterm.Red);
}
}
}Задача 4.2.Предъявите такие действительные (типа double ) числа  ,
,  и
и  такие,
что
такие,
что 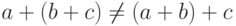 .
.
Достаточно вспомнить, что точки множества  расположены
на числовой прямой неравномерно.
расположены
на числовой прямой неравномерно.
Текст программы
public class DblNoAssociative {
public static void main(String[] args) {
double x = 1.0e-16;
double y = 1. + (x + x);
double z = (1. + x) + x ;
if (y != z) {
Xterm.print("Для числа ");
Xterm.print("x = " + x, Xterm.Blue);
Xterm.print(" величины 1.+(x+x) и (1.+x)+x ");
Xterm.print("различны\n", Xterm.Red);
Xterm.print("и равны соответственно");
Xterm.print(" " + y, Xterm.Red);
Xterm.print(" и");
Xterm.print(" " + z + "\n", Xterm.Red);
}
}
}Иногда даже работа с казалось бы не слишком маленькими или огромными по абсолютной величине числами может привести к удивительным результатам. Рассмотрим задачу о решении квадратного уравнения.
Задача Напишите программу, вводящую действительные коэффициенты  ,
,  и
и  квадратного уравнения
квадратного уравнения 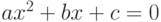 с положительным дискриминантом,
находящую оба корня этого уравнения.
с положительным дискриминантом,
находящую оба корня этого уравнения.
Вот вполне естественное решение этой задачи, которое может быть написано любым человеком, обладающим минимальными знаниями языка Java.
Текст программы
public class SquareEquation {
public static void main(String[] args) throws Exception {
double a = Xterm.inputDouble("Введите число a -> ");
double b = Xterm.inputDouble("Введите число b -> ");
double c = Xterm.inputDouble("Введите число c -> ");
if (a == 0.) {
Xterm.println("Уравнение не квадратное", Xterm.Red);
System.exit(0);
}
if (b*b - 4.*a*c <= 0.) {
Xterm.println("Дискриминант неположителен", Xterm.Red);
return;
}
double x1 = ( -b - Math.sqrt(b*b - 4.*a*c) ) / (2.*a);
double x2 = ( -b + Math.sqrt(b*b - 4.*a*c) ) / (2.*a);
Xterm.println("Корни уравнения:");
Xterm.println("x1 = " + x1, Xterm.Blue);
Xterm.println("x2 = " + x2, Xterm.Blue);
}
}Для извлечения квадратного корня здесь используется метод sqrt класса Math. Вызов метода System.exit и применение оператора return, которые в теле метода main почти эквивалентны и приводят к немедленному завершению выполнения программы, позволяет обойтись без ветви else оператора if-else. Остальная часть программы комментариев не требует.
Попробуйте, однако, выполнить эту программу при a=0.2E-16 и b=c=1.0 — первый корень уравнения x1 окажется равным -5.0E16, а второй x2 — нулю.
Если подставить эти значения в выражение  , то
и для x1 и для x2 его значение окажется равным единице, а не нулю.
Подобная ошибка для первого, весьма большого по величине корня,
представляется вполне естественной, но вот соглашаться с тем, что нуль
является корнем данного уравнения, совсем не хочется.
Этой проблеме посвящена одна из приведенных ниже задач.
, то
и для x1 и для x2 его значение окажется равным единице, а не нулю.
Подобная ошибка для первого, весьма большого по величине корня,
представляется вполне естественной, но вот соглашаться с тем, что нуль
является корнем данного уравнения, совсем не хочется.
Этой проблеме посвящена одна из приведенных ниже задач.

