|
Здравствуйте,при покупке печатной формы сертификата,будут ли выданы обе печатные сторны? |
Прикладные и теоретические методы программирования
5.2.2. Экспликативное, номинативное программирование
Экспликативное программирование (ЭП) ориентировано на разработку теории дескриптивных и декларативных программных формализмов, адекватных моделям структур данных, программ и средств конструирования из них программ [5.26-5.28]. Для этих структур решены проблемы существования, единства и эффективности. Теоретическую основу ЭП составляют логика, конструктивная математика, информатика, композиционное программирование и классическая теории алгоритмов. Для изображения алгоритмов программ используются алгоритмические языки и методы программирования: функциональное, логическое, структурное, денотационное и др.
Принципами ЭП являются:
- принцип развития понятия программы в абстрактном представлении и постепенной ее конкретизации с помощью экспликаций;
- принцип прагматичности или полезности определения понятия программы выполняется с точки зрения понятия "проблема" и ориентирован на решение задач пользователя;
- принцип адекватности ориентирован на абстрактное построение программ и реализацию проблемы с учетом информационности данных и апликативности. Программа рассматривается как функция, вырабатывающая выходные данные на основе входных данных. Функция - это объект, которому сопоставляется денотат имени функции с помощью отношения именования ( номинации ) ;
- принцип дескриптивности позволяет трактовать программу как сложные дескрипции, построенные из более простых и композиций отображения входных данных в результаты на основе п ринципа вычислимости.
Развитие понятия функции осуществляется с помощью принципа композиционности, т.е. составления программ (функций) из более простых программ для создания новых объектов с более сложными именами (дескрипциями) для функций. Они включают номинативные (именные) и языковые выражения, термы и формулы.
Таким образом, процесс развития программы осуществляется в виде цепочки понятий:
данные - функция - имя функции - композиция - дескрипция.
Из них триада - "данные - функция - композиция" задает семантический аспект программы, а триада "данные - имя функции - дескрипция" - синтаксический аспект. Главным в ЭП является семантический аспект, система композиций и номинативности (КНС), ориентированная на систематическое описание номинативных отношений при построении данных, функций, композиций и дескрипций [5.27].
КНС содержит специальные языковые системы для описания разнообразных классов функций, которые называются композиционно-номинативными языками функций. Такие системы тесно связаны с алгебрами функций и данных, построены в семантико- синтаксическом стиле. Они отличается от традиционных систем (моделей программ) теоретико-функциональным подходом, классами однозначных  -арных функций номинативными отображениями и структурами данных.
-арных функций номинативными отображениями и структурами данных.
Для построения математически простых и адекватных моделей программ параметрического типа используется КНС и методы универсальной алгебры, математической логики и теория алгоритмов. Данные в КНС рассматриваются на трех уровнях: абстрактном, булевском и номинативном. Класс номинативных данных обеспечивает построение именных данных, многозначных номинативных данных или мультиименных данных, задаваемых рекурсивно.
В рамках ЭП разработаны новые средства для определения систем данных, функций и композиций номинативного типа, имена аргументов которых принадлежат некоторому множеству имен  , т.е. композиция определяется на Z-номинативных наборах именных функций [5.29].
, т.е. композиция определяется на Z-номинативных наборах именных функций [5.29].
Номинативные данные позволяют задавать структуры данных, которым присущи неоднозначность именования компонентов типа множества, мультимножества, реляции и т.п.
Функции обладают свойством апликативности, их абстракции задают соответственно классы слабых и сильных аппликативных функций. Слабые функции позволяют задавать вычисление значений на множестве входных данных, а сильные - обеспечивают вычисление функций на заданных данных.
Композиции классифицируются уровнями данных и функций, а также типами аргументов. Экспликация композиций соответствует абстрактному рассмотрению функций как слабо аппликативных функций, и их уточнение строится на основе понятия детерминанта композиции как отображение специального типа. Класс аппликативных композиций предназначен для конструирования широкого класса программ.
Практическая проверка теоретического аппарата формализации дедуктивных и ОО БД прошла в ряде экспериментальных проектов в классе манипуляционных данных БД заданных в SQL-подобных языках.
5.2.3. Алгоритмика программ
Алгоритмика программ - структурная схемотология построения последовательных и параллельных программ с аппаратом формальных алгебраических преобразований и канонических форм описания логических и операторных выражений. Ее основу составляют системы алгебраических алгебр (САА), расширенные формализмами для представления логических условий параллельных программ и методами символьной мультиобработки [5.30].
Построение и исследование алгебры алгоритмов началось с проектирования логических структур ЭВМ под руководством академика В.М.Глушкова. В результате была построена теория САА, которая затем Г.Е.Цейтлиным была положена в основу создания обобщенной теории структурированных схем алгоритмов и программ, называемой алгоритмикой [5.30].
Основными понятиями алгебры алгоритмики являются:
- операции над множествами, булевы операции, предикаты, функции и операторы;
- бинарные и n-арные отношения, эквивалентность, частично и полностью упорядоченные множества;
- граф-схемы и операции над графовыми структурами;
- операции сигнатуры САА, аксиомы и правила вывода свойств программ на основе сверточной, разверточной и комбинированной стратегий;
- символьная обработка и методы синтаксического анализа программ.
Объекты алгоритмики - модели алгоритмов и программ, представляемые в виде схем. Метод алгоритмики базируется на компьютерной алгебре и логике и используется для проектирования алгоритмов прикладных задач. Построенные алгоритмы описываются в ЯП и реализуются соответствующими системами программирования в машинное представление.
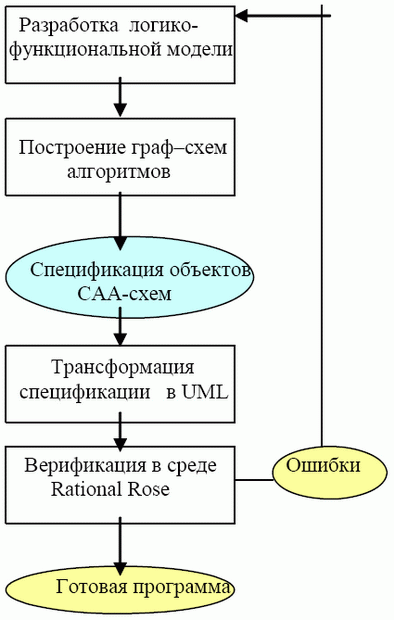
В рамках алгоритмики разработаны специальные инструментальные средства реализации алгоритмов программ, которые используют современные объектно-ориентированные средства и метод моделирования UML. Тем самым обеспечивается полный цикл работ по практическому применению разработанной теории алгоритмики для реализации прикладных задач, начиная с постановки задачи, формирования требований и разработки алгоритмов до получения программ решения этих задач (рис. 5.13).
Алгебра алгоритмов. Под алгеброй алгоритмов 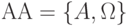 понимается основа
понимается основа  и сигнатура
и сигнатура  операций над элементами основы алгебры.
С помощью операции сигнатуры может быть получен произвольный элемент
операций над элементами основы алгебры.
С помощью операции сигнатуры может быть получен произвольный элемент 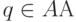 , который называется системой образующих алгебры.
, который называется системой образующих алгебры.
Если из этой системы не может быть исключен ни один элемент без нарушения ее свойств, то такая система образующих называется базисом алгебры.
Операции алгебры удовлетворяют следующим аксиоматическим законам: ассоциативности, коммутативности, идемпотентности, закону исключения третьего и противоречия. Алгебра, которой удовлетворяют перечисленные операции, называется булевой.
В алгебре алгоритмов используется алгебра множеств, элементами которой являются сами множества и операции над ними (объединение, пересечение, дополнение, универсум и др.).
Основные объекты алгебры алгоритимики - схемы алгоритмов и их суперпозиции, т.е. подстановки одних схем в другие. С подстановкой связана развертка, которая соответствует нисходящему процессу проектирования алгоритмов, и свертка. Т.е. переход к более высокому уровню спецификации алгоритма. Схемы алгоритмов соответствуют конструкциям структурного программирования.
Последовательное выполнение операторов  и
и 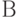 записывается в виде композиции
записывается в виде композиции  ; альтернативное выполнение операторов
; альтернативное выполнение операторов  и
и 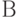 (
( 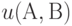 ) означает, если
) означает, если  истинно, то выполняется
истинно, то выполняется  ,иначе
,иначе 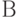 ; цикл
; цикл 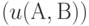 выполняется, пока не станет истинным условие
выполняется, пока не станет истинным условие  (
(  -логическая переменная).
-логическая переменная).
С помощью этих элементарных конструкций строится более сложная схема  алгоритма:
алгоритма:
![\begin{array}{l}
П ::= \{ [u_{1}] А_{1}\},\\
А_{1} ::= \{ [u_{2}] А_{2} * D\} \\
А_{2} ::= А_{3} * C, \\
А_{3} ::= \{ [u] А, B\}, \\
u :: = u_{2} \wedge u _{1}. \\
\end{array}](/sites/default/files/tex_cache/7f591998ffa6f67b82c803581e68b941.png)
Проведя суперпозицию путем свертки данной схемы алгоритма  , получаем формулу:
, получаем формулу:
![П ::= \{ [ u_{1}]\{[u_{2}]([u_{2} \wedge u _{1}] А, В) * С \} * D\}.](/sites/default/files/tex_cache/b99d0c200b0f3c133991b1391521b808.png)
Важный результат в области алгоритмики - проведение сопоставительного анализа аппарата алгебры алгоритмики с известными алгебрами. Дадим краткую характеристику.
Алгебра Дейкстры АД = 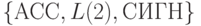 - двухосновная алгебра, элементами которой являются множество
- двухосновная алгебра, элементами которой являются множество  операторов, представленных структурными блок-схемами, множество
операторов, представленных структурными блок-схемами, множество 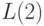 булевых функций в сигнатуре
булевых функций в сигнатуре 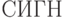 , в которую входят операции дизъюнкции, конъюнкции и отрицания, принимающие значения из
, в которую входят операции дизъюнкции, конъюнкции и отрицания, принимающие значения из 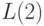 . С помощью специально разработанных механизмов преобразования АД в алгебру алгоритмики установлена связь между альтернативой и циклом, т.е.
. С помощью специально разработанных механизмов преобразования АД в алгебру алгоритмики установлена связь между альтернативой и циклом, т.е. ![\{[u] А\} = ([u] Е, А * \{[u] А\})](/sites/default/files/tex_cache/01e013eccafbc1e4faecd614f0b034ac.png) , произвольные операторы представлены суперпозицией основных операций и констант.
, произвольные операторы представлены суперпозицией основных операций и констант.
Операция фильтрации ![Ф(u) = \{[u] Е, N\}](/sites/default/files/tex_cache/2ec2f1c3617cc2b852e98f3947ee23c4.png) в АД представлена суперпозицией тождественного
в АД представлена суперпозицией тождественного 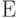 и неопределенного
и неопределенного  операторов и альтернативы алгебры алгоритмики,
где
операторов и альтернативы алгебры алгоритмики,
где  - фильтр разрешения выполнения операций вычислений.
- фильтр разрешения выполнения операций вычислений.
Оператор цикла  также представлен суперпозицией операций композиции и цикла в алгебре алгоритмики.
также представлен суперпозицией операций композиции и цикла в алгебре алгоритмики.
Алгебра схем Янова 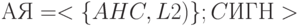 ,
где
,
где 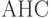 -совокупность неструктурных схем,
-совокупность неструктурных схем, 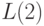 - совокупность различных булевских функций,
- совокупность различных булевских функций, 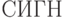 - сигнатура из композиции
- сигнатура из композиции  и операция неструктурного перехода
и операция неструктурного перехода 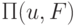 ,
а также операции дизъюнкции, конъюнкции и отрицания.
,
а также операции дизъюнкции, конъюнкции и отрицания. 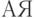 включает операции построения неструктурных логических схем программ.
Схема Янова состоит из предикатных символов множества
включает операции построения неструктурных логических схем программ.
Схема Янова состоит из предикатных символов множества 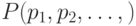 ,
операторных символов множества
,
операторных символов множества 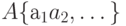 и графа переходов.
Оператор в данной алгебре - это пара
и графа переходов.
Оператор в данной алгебре - это пара 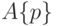 , состоящая из символов множества
, состоящая из символов множества  и множества предикатных символов.
Граф перехода представляет собой ориентированный граф, в вершинах которого располагаются преобразователи, распознаватели и один оператор останова.
Дуги графа задаются стрелками и помечаются они знаками
и множества предикатных символов.
Граф перехода представляет собой ориентированный граф, в вершинах которого располагаются преобразователи, распознаватели и один оператор останова.
Дуги графа задаются стрелками и помечаются они знаками 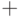 и
и  .
Преобразователь имеет один преемник, а распознаватель - два.
Каждый распознаватель включает в себя условие выполнения схемы.
Преобразователь обрабатывает операторы, включающие логические переменные, принадлежащие множеству
.
Преобразователь имеет один преемник, а распознаватель - два.
Каждый распознаватель включает в себя условие выполнения схемы.
Преобразователь обрабатывает операторы, включающие логические переменные, принадлежащие множеству 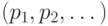 .
.
Каждая созданная схема 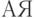 отличается большой сложностью, требует серьезного преобразования при переходе к представлению программы в виде соответствующей последовательности действий,
условий перехода и безусловного перехода. В работе [5.30] разработана теория интерпретации схем Янова и доказательство эквивалентности двух операторных схем исходя из особенностей алгебры алгоритмики.
отличается большой сложностью, требует серьезного преобразования при переходе к представлению программы в виде соответствующей последовательности действий,
условий перехода и безусловного перехода. В работе [5.30] разработана теория интерпретации схем Янова и доказательство эквивалентности двух операторных схем исходя из особенностей алгебры алгоритмики.
Для представления схемы Янова аппаратом алгебры алгоритмики сигнатура операций 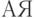 вводятся композиции
вводятся композиции  и операции условного перехода,
который в зависимости от условия
и операции условного перехода,
который в зависимости от условия  выполняет переход к следующим операторам или к оператору, помеченному меткой (типа
выполняет переход к следующим операторам или к оператору, помеченному меткой (типа  ).
Условный переход трактуется как бинарная операция
).
Условный переход трактуется как бинарная операция 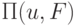 , которая зависит от условия
, которая зависит от условия  и разметок схемы
и разметок схемы  .
Кроме того, производится замена альтернативы и цикла типа
.
Кроме того, производится замена альтернативы и цикла типа  .
В результате выполнения бинарных операций получается новая схема
.
В результате выполнения бинарных операций получается новая схема  , в которой установлена
, в которой установлена  вместо метки и булевы операции конъюнкции и отрицания.
Эквивалентность выполненных операций преобразования обеспечивает правильность неструктурного представления.
вместо метки и булевы операции конъюнкции и отрицания.
Эквивалентность выполненных операций преобразования обеспечивает правильность неструктурного представления.
Система алгебр Глушкова 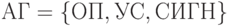 , где
, где 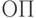 и
и 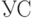 -
множества операторов суперпозиции, входящих в сигнатуру
-
множества операторов суперпозиции, входящих в сигнатуру 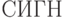 , и логических условий, определенных на информационном множестве
, и логических условий, определенных на информационном множестве  ,
,  , где
, где  - сигнатура операций Дейкстры,
- сигнатура операций Дейкстры, 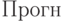 . - операция прогнозирования.
Сигнатура САА включает в себя операции алгебры АД, обобщенной трехзначной булевой операции и прогнозирования
(левое умножение условия на оператор
. - операция прогнозирования.
Сигнатура САА включает в себя операции алгебры АД, обобщенной трехзначной булевой операции и прогнозирования
(левое умножение условия на оператор  с порождением предиката
с порождением предиката  такого,
что
такого,
что 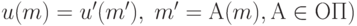 .
ИМ - множество обрабатываемых данных и определение операций из множеств ОП и УС.
Сущность операция прогнозирования состоит в проверке условия
.
ИМ - множество обрабатываемых данных и определение операций из множеств ОП и УС.
Сущность операция прогнозирования состоит в проверке условия  в состоянии
в состоянии  оператора
оператора  и определения условия
и определения условия 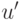 , вычисленного в состоянии
, вычисленного в состоянии 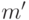 после выполнения оператора
после выполнения оператора  .
Данная алгебра ориентирована на аналитическую форму представления алгоритмов и оптимизацию алгоритмов по выбранным критериям.
.
Данная алгебра ориентирована на аналитическую форму представления алгоритмов и оптимизацию алгоритмов по выбранным критериям.
Алгебра булевых функций и связанные с ней теоремы о функциональной полноте и проблемы минимизации булевых функций также сведены до алгебры алгоритмики. Этот специальный процесс отличается громоздкостью и рассматриваться не будет, при необходимости можно обратиться к [5.30].
Алгебра алгоритмики и прикладные подалгебры.
Алгебра алгоритимки пополнена двухуровневой алгебраической системой и механизмами абстрактного описания данных (классами алгоритмов).
Под многоосновной алгоритмической системой (МАС) понимается система 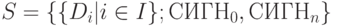 ,
где
,
где 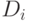 - основы или сорта,
- основы или сорта, 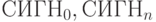 - совокупности операций и предикатов, определенных на
- совокупности операций и предикатов, определенных на 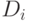 .
Если они пусты, то определяются многоосновные модели - алгебры.
Если сорта интерпретируются как множество обрабатываемых данных, то МАС представляет собой концепцию АТД, в виде подалгебры, широко используемую в объектном программировании.
Тем самым устанавливается связь с современными тенденциями развития современного программирования.
.
Если они пусты, то определяются многоосновные модели - алгебры.
Если сорта интерпретируются как множество обрабатываемых данных, то МАС представляет собой концепцию АТД, в виде подалгебры, широко используемую в объектном программировании.
Тем самым устанавливается связь с современными тенденциями развития современного программирования.
Практическим результатом исследований алгебры алгоритмики является построение оригинальных инструментальных систем проектирования алгоритмов и программ на основе современных средств поддержки ООП (Rational Rose). Детальное знакомство с данной темой можно продолжить, изучая приведенные ниже источники.
Контрольные вопросы и задания
- Дайте характеристику структурного метода программирования.
- Приведите основные особенности и возможности объектно-ориентированного программирования.
- Какие диаграммы имеются в языке UML для визуального проектирования программ?
- Приведите основные типы компонентов и пути их развития в компонентном программировании.
- Назовите базовые понятия в компонентном программировании.
- Приведите базовые структуры в компонентном программировании.
- Определите основные понятия и этапы жизненного цикла компонентного программирования.
- Определите основные элементы аспектно-ориентированного программирования.
- Определите основные элементы агентного программирования.
- Определите понятие агента и его место в программировании.
- Дайте характеристику инженерии ПрО.
- Определите объекты генерирующего программирования и дайте краткую характеристику.
- Что такое пространство проблем и пространство решений?
- Представьте теоретические методы программирования.
- Что такое алгоритмика и ее алгебра?
- Покажите сущность перехода от других алгебр к алгебре алгоритмики.