| Россия |
Рекуррентные сети: Ассоциативная память
Активная память
Выделение сигнала из шума
Разобучение действительно улучшает запоминание случайных образов. Однако, например, для коррелированных образов доводы, приведенные
в предыдущем разделе теряют свое значение. Действительно, если эти образы, например, являются слегка зашумленными вариантами одного
образа-прототипа 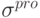 . Нетрудно показать, что в этом случае единственной зеркальной парой аттракторов в сети с Хеббовскими связями окажется
пара
. Нетрудно показать, что в этом случае единственной зеркальной парой аттракторов в сети с Хеббовскими связями окажется
пара 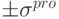 . Это означает, что вся память, которой обладает сеть, оказывается ложной. Отсюда следует, в частности, что состояниям ложной
памяти далеко не всегда соответствуют неглубокие энергетические минимумы.
. Это означает, что вся память, которой обладает сеть, оказывается ложной. Отсюда следует, в частности, что состояниям ложной
памяти далеко не всегда соответствуют неглубокие энергетические минимумы.
Этот пример показывает, что ложная память иногда не бесполезна, а преобразуя заучиваемые векторы, дает нам некоторую важную
информацию о них. В данном случае сеть как бы очищает ее от случайного шума. Подобное явление характерно и для обработки информации
человеком. В известном психологическом опыте людям предлагается запомнить изображения, каждое из которых представляет собой обязательно
искаженный равносторонний треугольник. При контрольной проверке на значительно более широком наборе образов, содержащийся в них
идеальный равносторонний треугольник опознается испытуемыми как ранее виденный. Такое явление называется выработкой прототипа.
Именно эта аналогия использовалась нами при введении обозначения 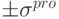 .
.
Минимальный базис
Состояния ложной памяти могут иметь и другие, не менее интересные формы. Рассмотрим, например, вариант модели Хопфилда, в котором
состояния нейронов принимают значения 0 или 1. Подобная модель легко переформулируется в оригинальную, для которой состояниями являются
спиновые переменные  , путем переопределения порогов. Мы, однако, будем считать, что в нашей сети пороги всех нейронов отрицательны и
бесконечно малы. Иначе говоря, динамика состояния нейрона определяется соотношениями
, путем переопределения порогов. Мы, однако, будем считать, что в нашей сети пороги всех нейронов отрицательны и
бесконечно малы. Иначе говоря, динамика состояния нейрона определяется соотношениями
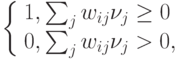
Рассмотрим следующий набор векторов:
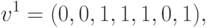
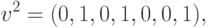
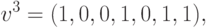
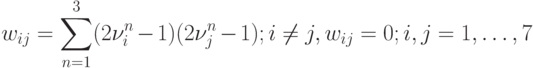
 ,
,  ,
, 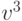 стационарными являются состояния, описываемые векторами
стационарными являются состояния, описываемые векторами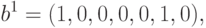
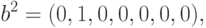
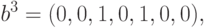
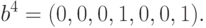
Векторы 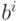 сами по себе замечательны. Их единичные компоненты помечают кооперированные нейроны, то есть те из них, которые
одновременно активны или одновременно пассивны во всех запоминаемых векторах
сами по себе замечательны. Их единичные компоненты помечают кооперированные нейроны, то есть те из них, которые
одновременно активны или одновременно пассивны во всех запоминаемых векторах 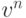 . Если считать, что компоненты векторов
. Если считать, что компоненты векторов 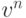 кодируют
некоторые признаки, то кооперированность некоторых нейронов означает, что некоторые признаки избыточны и могут быть заменены одним.
Например, если в нашем примере первый нейрон кодирует такое свойство, как пол, а шестой - наличие бороды, то практически со
стопроцентной вероятностью они могут быть заменены одним нейроном, о чем сигнализирует вектор
кодируют
некоторые признаки, то кооперированность некоторых нейронов означает, что некоторые признаки избыточны и могут быть заменены одним.
Например, если в нашем примере первый нейрон кодирует такое свойство, как пол, а шестой - наличие бороды, то практически со
стопроцентной вероятностью они могут быть заменены одним нейроном, о чем сигнализирует вектор 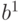 .
.
Векторы 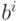 , кроме того, образуют так называемый минимальный базис. А именно, это минимальное число векторов, с помощью линейной
комбинации которых могут быть представлены все запоминаемые векторы
, кроме того, образуют так называемый минимальный базис. А именно, это минимальное число векторов, с помощью линейной
комбинации которых могут быть представлены все запоминаемые векторы
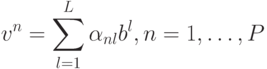
Кроме того, все стационарные состояния сети, в Хеббовские связи которых записаны векторы 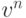 , также обязательно должны разлагаться
по векторам минимального базиса. Это означает, что если некоторые нейроны кооперированы в векторах
, также обязательно должны разлагаться
по векторам минимального базиса. Это означает, что если некоторые нейроны кооперированы в векторах 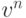 , то они должны кооперироваться и
во всех аттракторах сети.
, то они должны кооперироваться и
во всех аттракторах сети.
Используя векторы минимального базиса можно получить новый вид недиагональных элементов Хеббовской матрицы связей
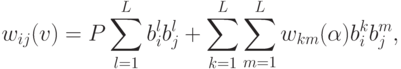
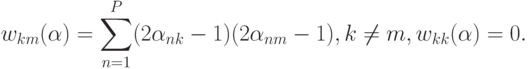
С помощью этого представления можно получить необходимые условия стационарности состояний сети. В частности, условие того, что
сеть будет генерировать в качестве аттракторов векторы минимального базиса, легко формулируется в терминах матричных элементов 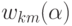 .
Именно,
.
Именно,  -му вектору базиса
-му вектору базиса 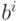 будет соответствовать стационарное состояние тогда и только тогда, когда все недиагональные элементы
будет соответствовать стационарное состояние тогда и только тогда, когда все недиагональные элементы  -й строки матрицы
-й строки матрицы 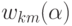 будут строго отрицательными.
будут строго отрицательными.
Для рассмотренного нами выше примера эта матрица имеет вид