| Россия, Москва |
Нечеткие и гибридные нейронные сети
Фазификатор
Фазификатор преобразует  -мерный вектор
-мерный вектор ![x = [x_1, x_2,
\ldots, x_N]](/sites/default/files/tex_cache/4569575be281c6c56564d4feaf71b46b.png) в нечеткое
множество
в нечеткое
множество  , характеризуемое функцией
принадлежности
, характеризуемое функцией
принадлежности  .
.
Наибольшей популярностью пользуются функции гауссовского типа, треугольные и трапецеидальные функции:
- Общая форма гауссовской функции
![\begin{align*}
\mu_A(x) = \exp[-(x-c)^2/\sigma^2]
\end{align*}](/sites/default/files/tex_cache/06ac6c5ba34a9b5935077135e14630db.png)
 - центр нечеткого множества,
- центр нечеткого множества, - коэффициент широты.
- коэффициент широты. - Симметричная треугольная функция
![\begin{align*}
\mu_A(x) = \{1 - |x-c|/d, \text{ при } x \in [c-d, c+d];\\
0, \text{ для остальных } x\},
\end{align*}](/sites/default/files/tex_cache/2c24bb7fcbccf8195bca699cc7a98efa.png)
 - центр,
- центр, - ширина.
- ширина. - Трапецеидальная функция
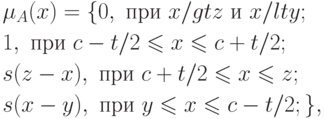
 - угол наклона.
- угол наклона.
При 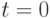 получаем треугольную функцию.
получаем треугольную функцию.
Дефазификатор
Трансформировать нечеткое множество 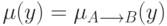 в точечное решение
в точечное решение  можно многими способами:
можно многими способами:
1. Дефазификация относительно центра области
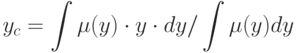
или
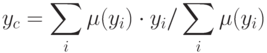
2. Дефазификация относительно среднего центра
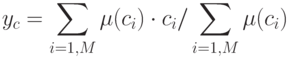
где 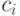 - центр
- центр  -го нечеткого правила,
-го нечеткого правила,
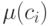 - соответствующая функция принадлежности.
- соответствующая функция принадлежности.
3. Дефазификация относительно среднего максимума
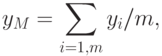
где  - количество точек, в которых
- количество точек, в которых 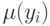 достигает максимального
значения. Если функция
достигает максимального
значения. Если функция 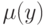 имеет максимальное значение только
в одной
точке, то
имеет максимальное значение только
в одной
точке, то
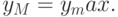
4. выбирается минимальное из максимальных значений  :
:
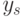 - наименьшее из
- наименьшее из  , для которых
, для которых  .
.
5. выбирается максимальное из максимальных значений:
 - наибольшее из
- наибольшее из  , для которых
, для которых  .
.
