| Россия, Москва |
Рекуррентные сети как ассоциативные запоминающие устройства
Обучение сети Хопфилда по правилу Хебба
Для одного обучающего вектора  значения весов могут быть
вычислены по
правилу Хебба
значения весов могут быть
вычислены по
правилу Хебба
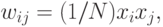
поскольку тогда
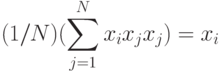
(вследствие биполярных значений элементов вектора  всегда
всегда  ).
).
При вводе большего количества обучающих векторов 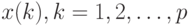 веса
веса  подбираются согласно обобщенному правилу Хебба
подбираются согласно обобщенному правилу Хебба
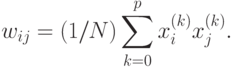
Важным параметром ассоциативной памяти является ее емкость. Под емкостью
понимается максимальное число запомненных образов, которые
классифицируются с допустимой погрешностью 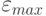 .
Показано, что при
использовании для обучения правила Хебба и при
.
Показано, что при
использовании для обучения правила Хебба и при  (1% компонентов
образа отличается от нормального состояния) максимальная емкость памяти
составит всего лишь около 13,8% от количества нейронов,
образующих
ассоциативную память. Столь малая емкость обусловлена тем, что сеть Хебба
хорошо запоминает только взаимно ортогональные векторы или близкие к ним.
(1% компонентов
образа отличается от нормального состояния) максимальная емкость памяти
составит всего лишь около 13,8% от количества нейронов,
образующих
ассоциативную память. Столь малая емкость обусловлена тем, что сеть Хебба
хорошо запоминает только взаимно ортогональные векторы или близкие к ним.
Обучение сети Хопфилда методом проекций
Лучшие результаты, чем при использовании правила Хебба, можно получить, если для обучения использовать псевдоинверсию. В основе этого подхода лежит предположение, что при правильно подобранных весах каждый поданный на вход сети вектор вызывает генерацию самого себя на выходе сети. В матричной форме это можно представить в виде
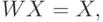
где  - матрица весов сети размерностью
- матрица весов сети размерностью  , а
, а  - прямоугольная
матрица размерностью
- прямоугольная
матрица размерностью  , составленная из
, составленная из  обучающих векторов
обучающих векторов 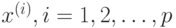 . Решение такой линейной системы уравнений имеет вид
. Решение такой линейной системы уравнений имеет вид
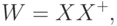
где знак + обозначает псевдоинверсию.
Если обучающие векторы линейно независимы, последнее выражение можно упростить и представить в виде
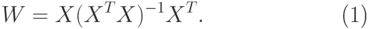 |
( 2) |
Здесь псевдоинверсия заменена обычной
инверсией квадратной матрицы  размерностью
размерностью  .
.
Выражение (2) можно записать в итерационной форме, не
требующей расчета
обратной матрицы. В этом случае (2) принимает вид итерационной
зависимости
от последовательности обучающих векторов 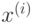 ,
, 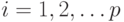 :
:

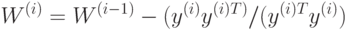
при начальных условиях 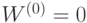 . В результате предъявления
. В результате предъявления  векторов матрица
весов сети принимает значение
векторов матрица
весов сети принимает значение 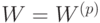 . Описанный здесь метод
называется
методом проекций. Применение его увеличивает максимальную емкость сети
Хопфилда до
. Описанный здесь метод
называется
методом проекций. Применение его увеличивает максимальную емкость сети
Хопфилда до 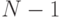 . Увеличение емкости обусловлено тем, что в
методе проекций
требование ортогональности векторов заменено гораздо менее жестким
требованием их линейной независимости.
. Увеличение емкости обусловлено тем, что в
методе проекций
требование ортогональности векторов заменено гораздо менее жестким
требованием их линейной независимости.
Модифицированный вариант метода проекций - метод  -проекций — градиентная
форма алгоритма минимизации. В соответствии с этим методом веса
подбираются с помощью процедуры, многократно повторяемой на всем множестве
обучающих векторов:
-проекций — градиентная
форма алгоритма минимизации. В соответствии с этим методом веса
подбираются с помощью процедуры, многократно повторяемой на всем множестве
обучающих векторов:

Обучающие векторы предъявляются многократно вплоть до стабилизации значений весов.
