|
Добрый день. Я приступила сегодня к самостоятельному изучению курса "Моделирование систем". Хочу понять - необходимо ли отсылать мои решения практических заданий на сайт, (и если да - то где найти волшебную кнопку "Загрузить...") или практические задания остаются полностью на моей совести? (никто не проверяет, и отчётности по ним я предоставлять не обязана?) P.S.: тьютора я не брала |
Инспектор
Вы можете этот курс.
Опубликован: 30.11.2010 | Уровень: специалист | Доступ: платный | ВУЗ: Мордовский государственный университет имени Н.П. Огарева
Лекция 1:
Моделирование многофазных систем массового обслуживания
2. Пример моделирования в системе GPSS/PC
Для моделирования в системе GPSS/PC необходимо подготовить данные по функциям распределения случайных величин для имитации пуассоновского входного потока и экспоненциального обслуживания. В обоих случаях используется экспоненциальное распределение, поскольку интервалы времени между требованиями в пуассоновском потоке распределены по экспоненциальному закону. В рассматриваемом случае параметры пуассоновского потока и экспоненциального обслуживания заданы и равны соответственно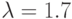 
, 
.
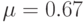Для подготовки данных по функциям распределения случайных величин использован следующий программный код:
clear all,clc
L = 1.7; %% Интенсивность входного потока
M = 0.67; %% Интенсивность обслуживания
%% Функции экспоненциального распределения
x = 0 : 0.2 : 20;
F = 1 - exp(-L*x);
F2 = 1 - exp(-M*x);
%%% Запись в текстовый файл input.txt
fid = fopen('input.txt', 'w');
%% Для блока generate
fprintf(fid, 'puas function RN1,C50\r\n');
for J = 1 : length(x)
if J <= 50
if mod(J, 5)
fprintf(fid, '%g,%g/', F(J), x(J));
else
fprintf(fid, '\r\n');
fprintf(fid, '%g,%g/', F(J), x(J));
end
end
end
fprintf(fid, '\r\n;-----------------------------------\r\n');
%% Для блоков advance
fprintf(fid, '\r\nexpM function RN2,C50\r\n');
for J = 1 : length(x)
if J <= 50
if mod(J, 5)
fprintf(fid, '%g,%g/', F2(J), x(J));
else
fprintf(fid, '\r\n');
fprintf(fid, '%g,%g/', F2(J), x(J));
end
end
end
fclose(fid);В программе функция 
применена для формирования заданного количества массива строк с данными для выбора случайных чисел, распределенных по экспоненциальному закону. Сформированные массивы будут представлены в GPSS-программе.
GPSS-программа приводится ниже. В ней задано условие обработки 500 требований.
Программный код решения примера в системе GPSS/PC:
simulate puas function RN5,C50 0,0/0.28823,0.2/0.493383,0.4/0.639405,0.6/ 0.743339,0.8/0.817316,1/0.869971,1.2/0.907449,1.4/0.934125,1.6/ 0.953112,1.8/0.966627,2/0.976246,2.2/0.983093,2.4/0.987966,2.6/ 0.991434,2.8/0.993903,3/0.995661,3.2/0.996911,3.4/0.997802,3.6/ 0.998435,3.8/0.998886,4/0.999207,4.2/0.999436,4.4/0.999598,4.6/ 0.999714,4.8/0.999797,5/0.999855,5.2/0.999897,5.4/0.999927,5.6/ 0.999948,5.8/0.999963,6/0.999974,6.2/0.999981,6.4/0.999987,6.6/ 0.99999,6.8/0.999993,7/0.999995,7.2/0.999997,7.4/0.999998,7.6/ 0.999998,7.8/0.999999,8/0.999999,8.2/0.999999,8.4/1,8.6/ 1,8.8/1,9/1,9.2/1,9.4/1,9.6/ 1,9.8/ ;------------------------------ expM function RN6,C50 0,0/0.12541,0.2/0.235092,0.4/0.331019,0.6/ 0.414916,0.8/0.488291,1/0.552465,1.2/0.60859,1.4/0.657677,1.6/ 0.700608,1.8/0.738154,2/0.770992,2.2/0.799712,2.4/0.82483,2.6/ 0.846798,2.8/0.866011,3/0.882815,3.2/0.897511,3.4/0.910364,3.6/ 0.921605,3.8/0.931437,4/0.940035,4.2/0.947556,4.4/0.954133,4.6/ 0.959885,4.8/0.964916,5/0.969316,5.2/0.973164,5.4/0.976529,5.6/ 0.979473,5.8/0.982047,6/0.984299,6.2/0.986268,6.4/0.98799,6.6/ 0.989496,6.8/0.990813,7/0.991965,7.2/0.992973,7.4/0.993854,7.6/ 0.994625,7.8/0.995299,8/0.995889,8.2/0.996404,8.4/0.996855,8.6/ 0.99725,8.8/0.997595,9/0.997896,9.2/0.99816,9.4/0.998391,9.6/ 0.998593,9.8/ tab1 table m1,0,5,12 tab2 table mp2,0,5,10 ******** Basic Program ******* 5 generate fn$puas 10 savevalue FULL+,1 ;--- Probability P00 ----------- 15 test E f1,0,met1 20 test E f2,0,met1 25 savevalue P_00+,1 ;--- Probability P01 ----------- 30 met1 test E f1,0,met2 35 savevalue P_01+,1 ;--- Probability P10 ----------- 40 met2 test E f2,0,met3; 45 savevalue P_10+,1 ;--- Probability P11+Pb1--------- 50 met3 test NE f1,0,met4 55 test NE f2,0,met4 60 test NE q2,0,met4 65 savevalue P_11b1+,1 70 met4 assign 2,1 75 gate NU 1,exitNOT ;---------- 1st phase --------------- 80 seize 1 85 advance fn$expM 90 release 1 95 mark 2 ;---------- Delay ------------------ 100 queue 2 105 gate NU 2 110 depart 2 120 tabulate tab2 ;---------- 2nd phase --------------- 125 seize 2 130 advance fn$expM 135 release 2 ;------------------------------------ 140 tabulate tab1 145 terminate 1 150 exitNOT savevalue exit0+,1 155 terminate start 500 ;end
Комментарии к программе
- Введение таблицы
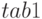с аргументом 
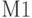(системный стандартный числовой атрибут) — временем пребывания в модели транзакта, обрабатываемого программой в данный момент, позволяет табулировать величину 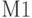и найти среднее значение времени пребывания транзакта в модели. - Введение таблицы
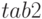с аргументом 
(стандартный числовой атрибут транзакта) — значением времени, равного разности относительного модельного времени и содержимого 2-го параметра текущего транзакта. Табулируется время пребывания транзакта в заблокированном состоянии. Отметка времени осуществляется блоком 
. - В программе использованы стандартные числовые атрибуты
, 
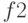, которые определяют состояния соответствующих устройств. Если устройство свободно, то величина стандартного числового атрибута равна 0, и 1 — во всех остальных случаях.
Результат выполнения программы система GPSS/PC оформляет в виде файла стандартного отчета, который имеет следующий вид:
GPSS/PC Report file REPORT.GPS. (V 2, # 37349) 01-08-2010 10:28:19 page 1
START_TIME END_TIME BLOCKS FACILITIES STORAGES FREE_MEMORY
0 675 30 2 0 135296
LINE LOC BLOCK_TYPE ENTRY_COUNT CURRENT_COUNT RETRY
5 1 GENERATE 3092 0 0
10 2 SAVEVALUE 3092 0 0
15 3 TEST 3092 0 0
20 4 TEST 501 0 0
25 5 SAVEVALUE 159 0 0
30 MET1 TEST 3092 0 0
35 7 SAVEVALUE 501 0 0
40 MET2 TEST 3092 0 0
45 9 SAVEVALUE 982 0 0
50 MET3 TEST 3092 0 0
55 11 TEST 2591 0 0
60 12 TEST 1768 0 0
65 13 SAVEVALUE 1453 0 0
70 MET4 ASSIGN 3092 0 0
75 15 GATE 3092 0 0
80 16 SEIZE 501 0 0
85 17 ADVANCE 501 1 0
90 18 RELEASE 500 0 0
95 19 MARK 500 0 0
100 20 QUEUE 500 0 0
105 21 GATE 500 0 0
110 22 DEPART 500 0 0
120 23 TABULATE 500 0 0
125 24 SEIZE 500 0 0
130 25 ADVANCE 500 0 0
135 26 RELEASE 500 0 0
140 27 TABULATE 500 0 0
145 28 TERMINATE 500 0 0
150 EXITNOT SAVEVALUE 2591 0 0
155 30 TERMINATE 2591 0 0
FACILITY ENTRIES UTIL. AVE._TIME AVAILABLE OWNER PEND INTER RETRY DELAY
1 501 0.800 1.08 1 3090 0 0 0 0
2 500 0.740 1.00 1 0 0 0 0 0
QUEUE MAX CONT. ENTRIES ENTRIES(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY
2 19 0 500 207 2.95 3.98 6.79 0
TABLE MEAN STD.DEV. RETRY RANGE FREQUENCY CUM.%
TAB1 6.06 5.22 0
- 0 50 10.00
0 - 5 233 56.60
5 - 10 120 80.60
10 - 15 67 94.00
15 - 20 24 98.80
20 - 25 6 100.00
TAB2 3.98 5.03 0
- 0 207 41.40
0 - 5 137 68.80
5 - 10 97 88.20
10 - 15 40 96.20
15 - 20 18 99.80
20 - 25 1 100.00
XACT_GROUP GROUP_SIZE RETRY
POSITION 0 0
GPSS/PC Report file REPORT.GPS. (V 2, # 37349) 01-08-2010 10:28:19 page 2
SAVEVALUE VALUE RETRY
FULL +3092 0
P_00 +159 0
P_01 +501 0
P_10 +982 0
P_11B1 +1453 0
EXIT0 +2591 0Расчет операционных характеристик двухфазной системы по файлу стандартного отчета будем на окончании помечать буквой 
.
Расчет вероятности отказа в обслуживании определим как отношение числа требований, получивших отказ (число 2591 в сохраняемой ячейке 
), к общему числу (число 3092 в сохраняемой ячейке 
):
.
Относительная пропускная способность и вероятность того, что вновь поступившее требование будет принято на обслуживание 1-й фазой, равны между собой и определяются как противоположная вероятность отказа в обслуживании, т. е.
.
Расчет эффективной частоты поступления требований в систему:
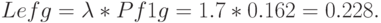
Абсолютная пропускная способность двухфазной системы:
.
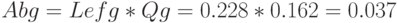Полное время пребывания требования в системе определяется как среднее значение таблицы с именем :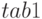
.
Среднее время блокировки 1-й фазы определяется как среднее значение таблицы с именем :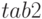
.
Среднее время обработки одного требования в двухфазной системе можно определить двумя путями: как сумму значений полей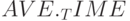 
для устройств 1 и 2 ( 
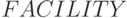) и как разность между 
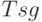и 
:
.
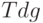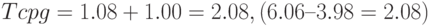Среднее число требований в двухфазной системе определим по формуле Литтла:
.
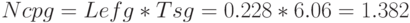Финальные (стационарные) вероятности определим как частное от деления числа требований, отвечающим заданным условиям (успешное событие), к общему числу требований, поступивших в систему. Для этого в программе были созданы ячейки сохраняемых величин: для вероятности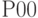 
— ячейка 
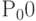, для вероятности 
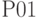— ячейка 
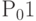, для вероятности 
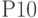— ячейка 
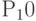, для суммы вероятностей 
(поскольку они равны между собой) — ячейка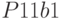 
. В соответствии с результатами, приведенными в файле стандартного отчета, получим
;
;
;
.
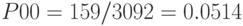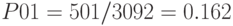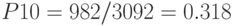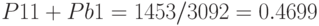Проведем контрольную проверку. Для этого сложим вероятности (которые являются несовместными):
.
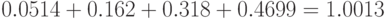Поскольку полученный результат практически равен единице, можно считать, что расчет вероятностей произведен успешно.
Задание 2
- Выполните прогон программы с датчиками случайных чисел
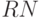в соответствии с номером компьютера, за которым выполняется лабораторная работа, т. е. 
, 
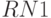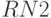и т. д. Сравните полученные операционные характеристики с соответствующими характеристиками, определенными при моделировании двухфазной системы в MATLAB. - Видоизмените программу так, чтобы можно было построить функцию распределения времени блокировки 1-й фазы.
- Напишите программу с различными интенсивностями обслуживания в фазах обслуживания. Рассчитайте также операционные характеристики двухфазной системы обслуживания. Сравните с операционными характеристиками, полученными при моделировании в системе MATLAB.
- Смоделируйте в MATLAB и в GPSS/PC (GPSS World) трехфазную систему обслуживания и рассчитайте операционные характеристики по параметрам примера для двухфазной системы, т. е. , .
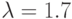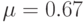Контрольные вопросы
- Каким видом дифференциальных уравнений описывается многофазная система массового обслуживания?
- Что называется интенсивностью входного потока требований?
- Что называется интенсивностью обслуживания многофазной системы?
- Что называется простейшим потоком требований?
- Что называется функцией распределения случайной величины?
- Какова функциональная связь между функцией распределения случайной непрерывной величины и ее плотностью?
- Могут ли быть многофазные системы с ожиданием? Если могут, то как будет выглядеть схема моделирования многофазной системы с ожиданием?
- Какие ограничения накладываются на численные значения интенсивности входного потока требований и интенсивности обслуживания в многофазной системе при ее моделировании?
- Сколько вы знаете аналогов формулы Литтла? Приведите известные вам формулы.
Мария Ястребинская
