|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Методы эколого-экономического анализа
Метод средних арифметических рангов. Сначала был применен метод средних арифметических рангов. Для этого прежде всего была подсчитана сумма рангов, присвоенных проектам (табл.8.1). Затем эта сумма была разделена на число экспертов, в результате рассчитан средний арифметический ранг (именно эта операция дала название методу). По средним рангам строится итоговая ранжировка (в другой терминологии - упорядочение), исходя из принципа - чем меньше средний ранг, чем лучше проект. Наименьший средний ранг, равный 2,625, у проекта Б, - следовательно, в итоговой ранжировке он получает ранг 1. Следующая по величине сумма, равная 3,125, у проекта М-К, - и он получает итоговый ранг 2. Проекты Л и Сол имеют одинаковые суммы (равные 3,25), значит, с точки зрения экспертов они равноценны (при рассматриваемом способе сведения вместе мнений экспертов), а потому они должны бы стоять на 3 и 4 местах и получают средний балл (3+4) /2 = 3,5. Дальнейшие результаты приведены в табл.20 ни же.
Итак, ранжировка по суммам рангов (или, что то же самое, по средним арифметическим рангам) имеет вид:
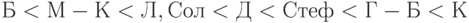 |
( 3) |
Здесь запись типа "А<Б" означает, что проект А предшествует проекту Б (т.е. проект А лучше проекта Б). Поскольку проекты Л и Сол получили одинаковую сумму баллов, то по рассматриваемому методу они эквивалентны, а потому объединены в группу (в фигурных скобках). В терминологии математической статистики ранжировка (3) имеет одну связь.
Метод медиан рангов. Значит, наука сказала свое слово, итог расчетов - ранжировка (3), и на ее основе предстоит принимать решение? Так был поставлен вопрос при обсуждении полученных результатов на заседании Правления фирмы. Но тут наиболее знакомый с современной эконометрикой член Правления вспомнил то, о чем шла речь в предыдущем разделе. Он вспомнил, что ответы экспертов измерены в порядковой шкале, а потому для них неправомерно проводить усреднение методом средних арифметических. Надо использовать метод медиан.
Что это значит? Надо взять ответы экспертов, соответствующие одному из проектов, например, проекту Д. Это ранги 5, 5, 1, 6, 8, 5, 6, 5, 6, 5, 7, 1. Затем их надо расположить в порядке неубывания (проще было бы сказать - "в порядке возрастания", но поскольку некоторые ответы совпадают, то приходится использовать непривычный термин "неубывание"). Получим последовательность: 1, 1, 5, 5, 5, 5, 5, 6, 6, 6, 7, 8. На центральных местах - шестом и седьмом - стоят 5 и 5. Следовательно, медиана равна 5.
| Д | Л | М-К | Б | Г-Б | Сол | Стеф | К | |
|---|---|---|---|---|---|---|---|---|
| Сумма рангов | 60 | 39 | 37,5 | 31.5 | 76 | 39 | 64 | 85 |
| Среднее арифметическое рангов | 5 | 3,25 | 3,125 | 2,625 | 6,333 | 3,25 | 5,333 | 7,083 |
| Итоговый ранг по среднему арифметическому | 5 | 3,5 | 2 | 1 | 7 | 3,5 | 6 | 8 |
| Медианы рангов | 5 | 3 | 3 | 2.25 | 7.5 | 4 | 6 | 7 |
| Итоговый ранг по медианам | 5 | 2.5 | 2.5 | 1 | 8 | 4 | 6 | 7 |
Медианы совокупностей из 12 рангов, соответствующих определенным проектам, приведены в предпоследней строке табл.8.2 (При этом медианы вычислены по обычным правилам статистики - как среднее арифметическое центральных членов вариационного ряда.) Итоговое упорядочение по методу медиан приведено в последней строке таблицы. Ранжировка (т.е. упорядочение - итоговое мнение комиссии экспертов) по медианам имеет вид:
 |
( 4) |
Поскольку проекты Л и М-К имеют одинаковые медианы баллов, то по рассматриваемому методу ранжирования они эквивалентны, а потому объединены в группу (кластер), т.е. с точки зрения математической статистики ранжировка (4) имеет одну связь.
Сравнение ранжировок по методу средних арифметических и методу медиан. Сравнение ранжировок (3) и (4) показывает их близость (похожесть). Можно принять, что проекты  упорядочены как
упорядочены как  , но из-за погрешностей экспертных оценок в одном методе признаны равноценными проекты
, но из-за погрешностей экспертных оценок в одном методе признаны равноценными проекты 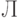 и
и  (ранжировка (3)), а в другом - проекты
(ранжировка (3)), а в другом - проекты  и
и 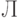 (ранжировка (4)). Существенным является только расхождение, касающееся упорядочения проектов
(ранжировка (4)). Существенным является только расхождение, касающееся упорядочения проектов  и
и 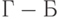 : в ранжировке (3)
: в ранжировке (3) 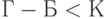 , а в ранжировке (4), наоборот,
, а в ранжировке (4), наоборот, 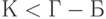 . Однако эти проекты - наименее привлекательные из восьми рассматриваемых, и при выборе наиболее привлекательных проектов для дальнейшего обсуждения и использования на указанное расхождение можно не обращать внимания.
. Однако эти проекты - наименее привлекательные из восьми рассматриваемых, и при выборе наиболее привлекательных проектов для дальнейшего обсуждения и использования на указанное расхождение можно не обращать внимания.
Рассмотренный пример демонстрирует сходство и различие ранжировок, полученных по методу средних арифметических рангов и по методу медиан, а также пользу от их совместного применения.
Метод согласования кластеризованных ранжировок. Проблема состоит в выделении общего нестрогого порядка из набора кластеризованных ранжировок (на статистическом языке - ранжировок со связями). Этот набор может отражать мнения нескольких экспертов или быть получен при обработке мнений экспертов различными методами. Предлагается метод согласования кластеризованных ранжировок, позволяющий "загнать" противоречия внутрь специальным образом построенных кластеров (групп), в то время как упорядочение кластеров соответствует одновременно всем исходным упорядочениям.
В различных прикладных областях возникает необходимость анализа нескольких кластеризованных ранжировок объектов. К таким областям относятся прежде всего экология, инженерный бизнес, менеджмент, экономика, социология, прогнозирование, научные и технические исследования и т.д., особенно те их разделы, что связаны с экспертными оценками. В качестве объектов могут выступать образцы продукции, технологии, математические модели, проекты, кандидаты на должность и др. Кластеризованные ранжировки могут быть получены как с помощью экспертов, так и объективным путем, например, при сопоставлении математических моделей с экспериментальными данными с помощью того или иного критерия качества. Мы разработали описанный ниже метод в связи с проблемами химической безопасности биосферы и экологического страхования.
В настоящем пункте рассматривается метод построения кластеризованной ранжировки, согласованной (в раскрытом ниже смысле) со всеми рассматриваемыми кластеризованными ранжировками. При этом противоречия между отдельными исходными ранжировками оказываются заключенными внутри кластеров согласованной ранжировки. В результате упорядоченность кластеров отражает общее мнение экспертов, точнее, то общее, что содержится в исходных ранжировках.
В кластеры заключены объекты, по поводу которых некоторые из исходных ранжировок противоречат друг другу. Для их упорядочения необходимо провести новые исследования. Эти исследования могут быть как формально-математическими (например, вычисление медианы Кемени, упорядочения по средним рангам или по медианам и т.п.), так и требовать привлечения новой информации из соответствующей прикладной области, возможно, проведения дополнительных научных или прикладных работ.
Введем необходимые понятия, затем сформулируем алгоритм согласования кластеризованных ранжировок в общем виде и рассмотрим его свойства.
Пусть имеется конечное число объектов, которые мы для простоты изложения будем изображать натуральными числами 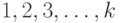 и называть их совокупность "носителем". Под кластеризованной ранжировкой, определенной на заданном носителе, понимаем следующую математическую конструкцию. Пусть объекты разбиты на группы, которые будем называть кластерами. В кластере может быть и один элемент. Входящие в один кластер объекты будем заключать в фигурные скобки. Например, объекты
и называть их совокупность "носителем". Под кластеризованной ранжировкой, определенной на заданном носителе, понимаем следующую математическую конструкцию. Пусть объекты разбиты на группы, которые будем называть кластерами. В кластере может быть и один элемент. Входящие в один кластер объекты будем заключать в фигурные скобки. Например, объекты 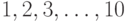 могут быть разбиты на 7 кластеров:
могут быть разбиты на 7 кластеров: 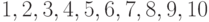 . В этом разбиении один кластер
. В этом разбиении один кластер 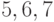 содержит три элемента, другой - {2,3} - два, остальные пять - по одному элементу. Кластеры не имеют общих элементов, а объединение их (как множеств) есть все рассматриваемое множество объектов (весь носитель).
содержит три элемента, другой - {2,3} - два, остальные пять - по одному элементу. Кластеры не имеют общих элементов, а объединение их (как множеств) есть все рассматриваемое множество объектов (весь носитель).
Вторая составляющая кластеризованной ранжировки - это строгий линейный порядок между кластерами. Задано, какой из них первый, какой второй, и т.д. Будем изображать упорядоченность с помощью знака < . При этом кластеры, состоящие из одного элемента, будем для простоты изображать без фигурных скобок. Тогда кластеризованную ранжировку на основе введенных выше кластеров можно изобразить так:
![А = [ 1 < {2,3} < 4 < {5,6,7} < 8 < 9 < 10 ].](/sites/default/files/tex_cache/b3ed2f52246d10168ae5f028611796ef.png)
Конкретные кластеризованные ранжировки будем заключать в квадратные скобки. Если для простоты речи термин "кластер" применять только к кластеру не менее чем из 2-х элементов, то можно сказать, что в кластеризованную ранжировку  входят два кластера {2,3} и {5,6,7} и 5 отдельных элементов.
входят два кластера {2,3} и {5,6,7} и 5 отдельных элементов.
Введенная описанным образом кластеризованная ранжировка является бинарным отношением на носителе - множестве 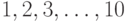 . Его структура такова. Задано отношение эквивалентности с 7-ю классами эквивалентности, а именно, {2,3}, {5,6,7}, а 5 классов остальные состоят из оставшихся 5 отдельных элементов. Затем введен строгий линейный порядок между классами эквивалентности.
. Его структура такова. Задано отношение эквивалентности с 7-ю классами эквивалентности, а именно, {2,3}, {5,6,7}, а 5 классов остальные состоят из оставшихся 5 отдельных элементов. Затем введен строгий линейный порядок между классами эквивалентности.
Введенный математический объект известен в литературе как "ранжировка со связями" (М. Холлендер, Д.Вулф), "упорядочение" (Дж. Кемени, Дж. Снелл), "квазисерия" (Б.Г.Миркин), "совершенный квазипорядок" (Ю.А.Шрейдер [5, с.127, 130]). Учитывая разнобой в терминологии, мы сочли полезным ввести собственный термин "кластеризованная ранжировка", поскольку в нем явным образом названы основные элементы изучаемого математического объекта - кластеры, рассматриваемые на этапе согласования ранжировок как классы эквивалентности, и ранжировка - строгий совершенный порядок между ними (в терминологии Ю.А.Шрейдера
Следующее важное понятие - противоречивость. Оно определяется для четверки - две кластеризованные ранжировки на одном и том же носителе и два различных объекта - элементы того же носителя. При этом два элемента из одного кластера будем связывать символом равенства = , как эквивалентные.
Пусть А и В - две кластеризованные ранжировки. Пару объектов 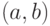 назовем "противоречивой" относительно кластеризованных ранжировок А и В, если эти два элемента по-разному упорядочены в
назовем "противоречивой" относительно кластеризованных ранжировок А и В, если эти два элемента по-разному упорядочены в  и
и 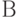 , т.е.
, т.е.  (первый вариант противоречивости) либо
(первый вариант противоречивости) либо  (второй вариант противоречивости). Отметим, что в соответствии с этим определением пара объектов
(второй вариант противоречивости). Отметим, что в соответствии с этим определением пара объектов 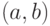 , эквивалентная хотя бы в одной кластеризованной ранжировке, не может быть противоречивой: эквивалентность a = b не образует "противоречия" ни с a < b, ни с a > b. Это свойство оказывается полезным при выделении противоречивых пар.
, эквивалентная хотя бы в одной кластеризованной ранжировке, не может быть противоречивой: эквивалентность a = b не образует "противоречия" ни с a < b, ни с a > b. Это свойство оказывается полезным при выделении противоречивых пар.
В качестве примера рассмотрим, кроме А, еще две кластеризованные ранжировки
![В = [{1,2} < { 3,4, 5} < 6 < 7 < 9 < {8, 10}],\\
C = [3 < {1, 4} < 2 < 6 < {5, 7, 8} < {9, 10}].](/sites/default/files/tex_cache/ace8c37996fd3276bb4493c1245cdde4.png)
Совокупность противоречивых пар объектов для двух кластеризованных ранжировок А и В назовем "ядром противоречий" и обозначим 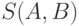 . Для рассмотренных выше в качестве примеров трех кластеризованных ранжировок
. Для рассмотренных выше в качестве примеров трех кластеризованных ранжировок 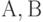 и
и  , определенных на одном и том же носителе
, определенных на одном и том же носителе 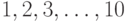 , имеем
, имеем
![S(A,B) = [ (8, 9)], S(A,C) = [ (1, 3), (2,4) ] ,\\
S(B,C) = [ (1, 3), (2, 3), (2, 4), (5, 6), (8,9) ].](/sites/default/files/tex_cache/e7f245d2cd662c673d5d1d9abb7b1bb2.png)
Как при ручном, так и при программном нахождении ядра можно в поисках противоречивых пар просматривать пары 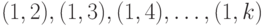 , затем
, затем 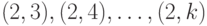 , потом
, потом 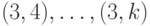 , и т.д., вплоть до последней пары
, и т.д., вплоть до последней пары 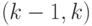 .
.
Пользуясь понятиями дискретной математики, "ядро противоречий" можно изобразить графом с вершинами в точках носителя. При этом противоречивые пары задают ребра этого графа. Граф для 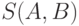 имеет только одно ребро (одна связная компонента более чем из одной точки), для
имеет только одно ребро (одна связная компонента более чем из одной точки), для 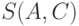 - 2 ребра (две связные компоненты более чем из одной точки), для
- 2 ребра (две связные компоненты более чем из одной точки), для 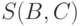 - 5 ребер (три связные компоненты более чем из одной точки, а именно, {1, 2 , 3, 4}, {5, 6} и {8, 9}).
- 5 ребер (три связные компоненты более чем из одной точки, а именно, {1, 2 , 3, 4}, {5, 6} и {8, 9}).
Каждую кластеризованную ранжировку, как и любое бинарное отношение, можно задать матрицей  из 0 и 1 порядка
из 0 и 1 порядка 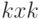 . При этом
. При этом 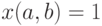 тогда и только тогда, когда
тогда и только тогда, когда 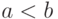 либо
либо 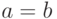 . В первом случае
. В первом случае 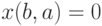 , а во втором
, а во втором 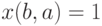 . При этом хотя бы одно из чисел
. При этом хотя бы одно из чисел 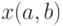 и
и 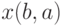 равно 1. Из определения противоречивости пары
равно 1. Из определения противоречивости пары 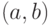 вытекает, что для нахождения всех таких пар достаточно поэлементно перемножить две матрицы
вытекает, что для нахождения всех таких пар достаточно поэлементно перемножить две матрицы  и
и 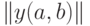 , соответствующие двум кластеризованным ранжировкам, и отобрать те и только те пары, для которых
, соответствующие двум кластеризованным ранжировкам, и отобрать те и только те пары, для которых 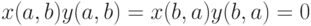 .
.
Предлагаемый алгоритм согласования некоторого числа (двух или более) кластеризованных ранжировок состоят из трех этапов. На первом выделяются противоречивые пары объектов во всех парах кластеризованных ранжировок. На втором формируются кластеры итоговой кластеризованной ранжировки (т.е. классы эквивалентности - связные компоненты графов, соответствующих объединению попарных ядер противоречий). На третьем этапе эти кластеры (классы эквивалентности) упорядочиваются. Для установления порядка между кластерами произвольно выбирается один объект из первого кластера и второй - из второго, порядок между кластерами устанавливается такой же, какой имеет быть между выбранными объектами в любой из рассматриваемых кластеризованных ранжировок. Корректность подобного упорядочивания, т.е. его независимость от выбора той или иной пары объектов, вытекает из соответствующих теорем.. Два объекта из разных кластеров согласующей кластеризованной ранжировки могут оказа ться эквивалентными в одной из исходных кластеризованных ранжировок (т.е. находиться в одном кластере). В таком случае надо рассмотреть упорядоченность этих объектов в какой-либо другой из исходных кластеризованных ранжировок. Если же во всех исходных кластеризованных ранжировках два рассматриваемых объекта находились в одном кластере, то естественно считать (и это является уточнением к этапу 3 алгоритма), что они находятся в одном кластере и в согласующей кластеризованной ранжировке.
Результат согласования кластеризованных ранжировок 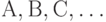 обозначим
обозначим 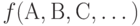 . Тогда
. Тогда
![f(А, В) = [1<2<3<4<5<6<7<\{8, 9\}<10],\\
f(А, С) = [\{1,3\}<\{2, 4\}<6<\{5,7\}<8<9<10],\\
f(В, С) = [\{1,2,3,4\}<\{5,6\}<7<\{8,9\}<10],\\
f(А, В, С) = f(В, С) = [\{1,2,3,4\} <\{5,6\}<7<\{8, 9\}<10].](/sites/default/files/tex_cache/fe9f17d6bd23b72d84936ed7bbe9b11c.png)
В случае 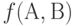 дополнительного изучения с целью упорядочения требуют только объекты 8 и 9. В случае
дополнительного изучения с целью упорядочения требуют только объекты 8 и 9. В случае 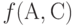 кластер {5,7} появился не потому, что относительно объектов 5 и 7 имеется противоречие, а потому, что в обеих исходных ранжировках эти объекты не различаются. В случае
кластер {5,7} появился не потому, что относительно объектов 5 и 7 имеется противоречие, а потому, что в обеих исходных ранжировках эти объекты не различаются. В случае 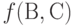 объекты 1,2,3,4 объединились в один кластер, т.е. кластеризованные ранжировки оказались настолько противоречивыми, что процедура согласования не позволила провести достаточно полную декомпозицию задачи нахождения итогового мнения экспертов.
объекты 1,2,3,4 объединились в один кластер, т.е. кластеризованные ранжировки оказались настолько противоречивыми, что процедура согласования не позволила провести достаточно полную декомпозицию задачи нахождения итогового мнения экспертов.
Рассмотрим некоторые свойства алгоритмов согласования.
1. Пусть 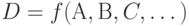 . Если
. Если  в согласующей кластеризованной ранжировке D, то a<b или a=b в каждой из исходных ранжировок
в согласующей кластеризованной ранжировке D, то a<b или a=b в каждой из исходных ранжировок 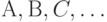 , причем хотя бы в одной из них справедливо строгое неравенство.
, причем хотя бы в одной из них справедливо строгое неравенство.
2. Построение согласующих кластеризованных ранжировок может осуществляться поэтапно. В частности, 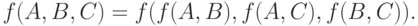 Ясно, что ядро противоречий для набора кластеризованных ранжировок является объединением таких ядер для всех пар рассматриваемых ранжировок
Ясно, что ядро противоречий для набора кластеризованных ранжировок является объединением таких ядер для всех пар рассматриваемых ранжировок
3. Построение согласующих кластеризованных ранжировок нацелено на выделение общего упорядочения в исходных кластеризованных ранжировках. Однако при этом некоторые общие свойства исходных кластеризованных ранжировок могут теряться. Так, при согласовании ранжировок В и С, рассмотренных выше, противоречия в упорядочении элементов 1 и 2 не было - в ранжировке В эти объекты входили в один кластер, т.е. 1 = 2, в то время как 1<2 в кластеризованной ранжировке С. Значит, при их отдельном рассмотрении можно принять упорядочение 1<2. Однако в f(В,C) они попали в один кластер, т.е. возможность их упорядочения исчезла. Это связано с поведением объекта 3, который "перескочил" в С на первое место и "увлек с собой в противоречие" пару (1, 2), образовав противоречивые пары и с 1, и с 2. Другими словами, связная компонента графа, соответствующего ядру противоречий, сама по себе не всегда является полным графом. Недостающие ребра при этом соответствуют парам типа (1, 2), которые сами по себе не являются противоречивыми, но "увлекаются в противоречие" другими парами.
4. Необходимость согласования кластеризованных ранжировок возникает, в частности, при разработке методики применения экспертных оценок в задачах экологического страхования и химической безопасности биосферы. Как уже говорилось, популярным является метод упорядочения по средним рангам, в котором итоговая ранжировка строится на основе средних арифметических рангов, выставленных отдельными экспертами. Однако из теории измерений известно (см. выше), что более обоснованным является использование не средних арифметических, а медиан. Вместе с тем метод средних рангов весьма известен и широко применяется, так что просто отбросить его нецелесообразно. Поэтому было принято решение об одновременном применении обеих методов. Реализация этого решения потребовала разработки методики согласования двух указанных кластеризованных ранжировок.
5. Область применения рассматриваемого метода не ограничивается экспертными оценками. Он может быть использован, например, для сравнения качества математических моделей процесса испарения жидкости. Имелись данные экспериментов и результаты расчетов по 8 математическим моделям. Сравнивать модели можно по различным критериям качества. Например, по сумме модулей относительных отклонений расчетных и экспериментальных значений. Можно и по другому - в каждой экспериментальной точке упорядочить модели по качеству, а потом получать единую оценку методами средних рангов и медиан. Использовались и иные методы. Затем применялись методы согласования полученных кластеризованных ранжировок. В результате оказалось возможным упорядочить модели по качеству и использовать это упорядочение при разработке банка математических моделей, используемого в задачах химической безопасности биосферы.
6. Рассматриваемый метод согласования кластеризованных ранжировок построен в соответствии с методологией теории устойчивости, согласно которой результат обработки данных, инвариантный относительно метода обработки, соответствует реальности, а результат расчетов, зависящий от метода обработки, отражает субъективизм исследователя, а не объективные соотношения.
