|
Упражнение 2.1.25 |
Автоматы с магазинной памятью
Подобно тому, как праволинейным грамматикам соответствуют конечные автоматы, контекстно-свободным грамматикам соответствуют автоматы с магазинной памятью (МП-автоматы). В таком автомате, помимо ограниченной памяти, хранящей текущее состояние, имеется потенциально бесконечная память, используемая как стек (магазин), то есть структура данных, где в каждый момент доступен только тот элемент, который был добавлен позже остальных присутствующих на данный момент элементов.
Для наглядности стек обычно изображают вертикально, так, что доступный элемент данных (вершина) находится наверху. Но при формальном определении конфигурации (мгновенного состояния) МП-автомата удобно считать все содержимое стека конечной последовательностью символов, то есть словом (в алфавите, в котором перечислены все возможные данные, "умещающиеся" в одной ячейке стека). Прежде чем определить конфигурацию, придется принять произвольное соглашение о том, в каком порядке записывать содержимое стека в этом слове. В этой книге считается, что вершина стека находится в начале слова (то есть слева). В разделе 10.1 даются необходимые определения. В разделе 10.2 доказывается, что МП-автоматы распознают в точности контекстно-свободные языки.
10.1. Определение автомата с магазинной памятью
Определение 10.1.1. Автомат с магазинной памятью
( МП-автомат, магазинный автомат, стековый автомат,
pushdown automaton) -
это шестерка 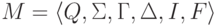 ,
где
,
где  ,
,  ,
,  и
и  - конечные множества,
- конечные множества, 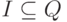 ,
,  и
и
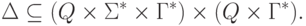
 - входной алфавит,
- входной алфавит,  - алфавит магазинной памяти
(stack alphabet),
- алфавит магазинной памяти
(stack alphabet),  - множество переходов
(transition relation), элементы I
называются начальными состояниями,
элементы F - заключительными
или допускающими
состояниями.
- множество переходов
(transition relation), элементы I
называются начальными состояниями,
элементы F - заключительными
или допускающими
состояниями.Пример 10.1.2.
Пусть Q = {1,2}, 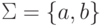 ,
, 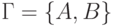 ,
,
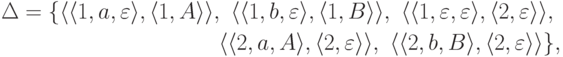
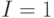 ,
,  .
Тогда
.
Тогда 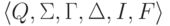 -
МП-автомат.
-
МП-автомат.Замечание 10.1.3.
МП-автоматы можно изображать в виде диаграмм состояний.
На диаграмме каждое состояние обозначается кружком,
а переход - стрелкой.
Каждое начальное состояние распознается
по ведущей в него короткой стрелке.
Каждое допускающее состояние отмечается на диаграмме
двойным кружком.
Стрелка с пометкой 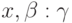 ,
ведущая из p в q,
показывает, что
,
ведущая из p в q,
показывает, что 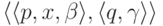 является переходом данного МП-автомата.
является переходом данного МП-автомата.
Пример 10.1.4. Ниже приведена диаграмма МП-автомата из примера 10.1.2.
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{a,\varepsilon:A}
\rloop{0,-1} ^{b,\varepsilon:B}
\ar "1,2" ^{\varepsilon,\varepsilon:\varepsilon}
& *=[o][F=]{2}
\rloop{0,1} ^{a,A:\varepsilon}
\rloop{0,-1} ^{b,B:\varepsilon}
}](/sites/default/files/tex_cache/6812559f1df4c3fae5e60dbf586f2634.png)
Определение 10.1.5. Конфигурацией
МП-автомата называется любая тройка 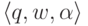 ,
где
,
где 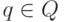 ,
, 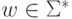 ,
, 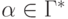 .
.
Определение 10.1.6.
Определим на множестве всех конфигураций МП-автомата 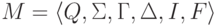 бинарное отношение
бинарное отношение 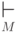 ( такт работы )
следующим образом.
Если
( такт работы )
следующим образом.
Если  ,
, 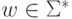 и
и 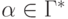 ,
то
,
то 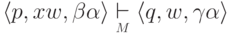 .
.
Замечание 10.1.7
Обычно из контекста ясно, о каком
МП-автомате идет речь.
Тогда вместо 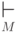 будем писать
будем писать 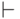 .
.
Пример 10.1.8.
Для МП-автомата
из примера 10.1.2
выполняется 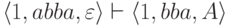 и
и 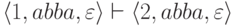 .
.
Определение 10.1.9.
Бинарное отношение 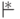 определяется как рефлексивное, транзитивное замыкание
отношения
определяется как рефлексивное, транзитивное замыкание
отношения 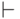 .
.
Пример 10.1.10.
Для МП-автомата
из примера 10.1.2
выполняется 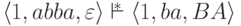 и
и 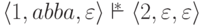 .
.
Лемма 10.1.11. Если 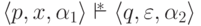 и
и 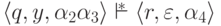 , то
, то 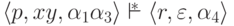 .
.
Доказательство.
Лемму легко доказать индукцией
по количеству тактов в вычислительном процессе,
ведущем из конфигурации 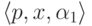 в конфигурацию
в конфигурацию 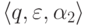 .
.
Определение 10.1.12.
Слово 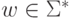 допускается
МП-автоматом
допускается
МП-автоматом 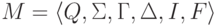 ,
если
найдутся такие состояния
,
если
найдутся такие состояния 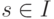 и
и  ,
что
,
что 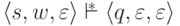 .
.
Определение 10.1.13. Язык, распознаваемый МП-автоматом, - множество всех слов, допускаемых этим МП-автоматом. Язык, распознаваемый МП-автоматом M, обозначается L(M).
Замечание 10.1.14. Обычно в учебниках используется более узкое определение МП-автомата, но это не меняет класса языков, распознаваемых МП-автоматами.
Пример 10.1.15.
Пусть  -
МП-автомат из примера 10.1.2.
Тогда
-
МП-автомат из примера 10.1.2.
Тогда 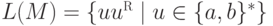 .
.
Пример 10.1.16.
Пусть 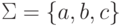 .
Рассмотрим МП-автомат
.
Рассмотрим МП-автомат 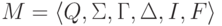 ,
где
,
где 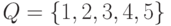 ,
,  , I = {1}, F = {4,5}
и
, I = {1}, F = {4,5}
и
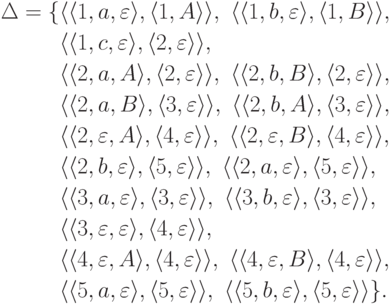
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix @=11mm{
%
&
&
& *=[o][F-]{3}
\rloop{0,1} ^{a,\varepsilon:\varepsilon}
\rloop{0,-1} ^{b,\varepsilon:\varepsilon}
\ar "2,5" ^-(.2){\varepsilon,\varepsilon:\varepsilon}
&
\\
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{a,\varepsilon:A}
\rloop{0,-1} ^{b,\varepsilon:B}
\ar "2,2" ^{c,\varepsilon:\varepsilon}
& *=[o][F-]{2}
\rloop{0,1} ^{a,A:\varepsilon}
\rloop{0,-1} ^{b,B:\varepsilon}
\ar "1,4" <0.6mm> ^{a,B:\varepsilon}
\ar "1,4" <-0.6mm> _{b,A:\varepsilon}
\ar "2,5" <0.6mm> ^{\varepsilon,A:\varepsilon}
\ar "2,5" <-0.6mm> _{\varepsilon,B:\varepsilon}
\ar "3,4" <0.6mm> ^{a,\varepsilon:\varepsilon}
\ar "3,4" <-0.6mm> _{b,\varepsilon:\varepsilon}
&
&
& *=[o][F=]{4}
\rloop{0,1} ^{\varepsilon,A:\varepsilon}
\rloop{0,-1} ^{\varepsilon,B:\varepsilon}
\\
%
&
&
& *=[o][F=]{5}
\rloop{0,1} ^{a,\varepsilon:\varepsilon}
\rloop{0,-1} ^{b,\varepsilon:\varepsilon}
&
}](/sites/default/files/tex_cache/f63795b364e3cb308b33b8d16a6a409c.png)
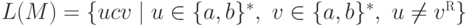 .
.Определение 10.1.17. Два МП-автомата эквивалентны, если они распознают один и тот же язык.
Замечание 10.1.18. В данном пособии не рассматриваются преобразователи с магазинной памятью (pushdown transducer) обобщение автоматов с магазинной памятью посредством добавления "выходного" потока (см. [7, 3.5] или [2, 3.1.4]).
Замечание 10.1.19.
Некоторые авторы
изменяют определение допускаемых слов следующим образом:
слово w допускается МП-автоматом 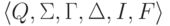 ,
если найдутся такие состояния
,
если найдутся такие состояния 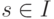 и
и  и последовательность
и последовательность 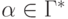 ,
что
,
что 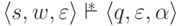 .
Такое определение
не изменяет класса языков, распознаваемых
МП-автоматами.
.
Такое определение
не изменяет класса языков, распознаваемых
МП-автоматами.
Замечание 10.1.20.
Некоторые авторы
добавляют в определение МП-автомата
седьмую компоненту - Z0, называемую маркером магазинной памяти
(start pushdown symbol),
и изменяют определение допускаемых слов следующим образом:
слово w допускается МП-автоматом 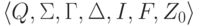 ,
если найдутся такие состояния
,
если найдутся такие состояния 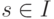 и
и  ,
что
,
что 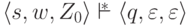 .
Такое определение
не изменяет класса языков, распознаваемых МП-автоматами.
.
Такое определение
не изменяет класса языков, распознаваемых МП-автоматами.
Замечание 10.1.21.
Класс языков, распознаваемых МП-автоматами,
не изменится также, если использовать следующую естественную комбинацию
двух предыдущих определений:
слово w допускается МП-автоматом 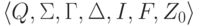 ,
если найдутся такие состояния
,
если найдутся такие состояния 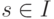 и
и  и последовательность
и последовательность 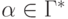 ,
что
,
что 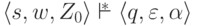 .
.
Замечание 10.1.22.
Некоторые авторы
добавляют в определение МП-автомата
маркер магазинной памяти Z0,
отбрасывают множество F
и изменяют определение допускаемых слов следующим образом:
слово w допускается МП-автоматом 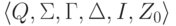 ,
если
найдутся такие состояния
,
если
найдутся такие состояния 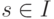 и
и 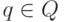 ,
что
,
что 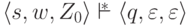 .
Это также не изменяет класса языков, распознаваемых
МП-автоматами.
.
Это также не изменяет класса языков, распознаваемых
МП-автоматами.
Упражнение 10.1.23. Найти МП-автомат, распознающий язык 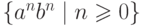
Упражнение 10.1.24. Найти МП-автомат, распознающий язык 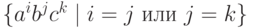
Упражнение 10.1.25. Найти МП-автомат, распознающий язык 

