Рекурсивные программы

9.3. Контракты рекурсивных программ

Мы уже научились поставлять наши классы и их методы с контрактами, устанавливающими их корректность: предусловия и постусловия методов, инварианты класса. Те же подходы, применяемые к алгоритмам, приводят к заданию вариантов и инвариантов цикла. Как рекурсия вписывается в эту картину?

Мы уже познакомились с понятием варианта для рекурсии. Если метод рекурсивен непосредственно или косвенно, то следует включать вариант для рекурсии в его описание. Как отмечалось, специальный синтаксис для этих целей отсутствует, так что приходится добавлять отдельное предложение в заголовочный комментарий метода:

— variant: expression
    

Рекурсивный метод, подобно всякому методу, может иметь предусловие и постусловие. Поскольку ответственность за проверку предусловия всегда лежит на клиенте – вызывающей программе, а в данном случае клиентом является сам рекурсивный метод, то новинкой будет необходимость убедиться, что все рекурсивные вызовы внутри метода (для косвенной рекурсии – в ассоциированных методах) удовлетворяют предусловию.

Вот пример процедуры Hanoi с более полными контрактами, новыми предложениями, записанными в виде комментариев:

hanoi (n: INTEGER; source, target, other: CHARACTER)
        —Перенос n дисков из source на target,используя other
        —в соответствии с правилами игры Ханойская Башня
        — invariant: диски на каждом стержне образуют пирамиду,
        — следуя в порядке уменьшения размеров.
        — variant: n
    require
        non_negative: n >= 0
        different1: source /= target
        different2: target /= other
        different3: source /= other
        — source имеет n дисков; target и other пусты – без дисков
    do
        if n > 0 then
            hanoi (n–1, source, other, target)
            move (source, target)
            hanoi (n–1, other, target, source)
        end
    ensure
        — Диски, ранее находившиеся на source, теперь перенесены на target,
        — сохраняя прежний порядок,
        — other находится в исходном состоянии.
    end
—invariant: текст комментария
    

Предлагаемая конструкция не является частью языка, но подчиняется следующим соглашениям.

• Если инвариант рекурсии является псевдокодом, заданным комментарием, как в данном примере, то он не повторяется в предусловии и постусловии, (здесь это означает, что в предусловии и постусловии ничего не говорится о требованиях сортировки дисков по размерам).
• Любое формальное предложение инварианта рекурсии (булевское выражение) должно включаться в предусловие и постусловие.

9.4. Реализация рекурсивных программ

Рекурсивное программирование хорошо работает в некоторых проблемных областях, что проиллюстрировано примерами этой лекции. Когда рекурсия облегчает вашу работу, нужно применять ее, не раздумывая, так как в современных языках программирования рекурсия считается само собой разумеющейся.

Обычно на уровне машинного кода отсутствует прямая поддержка рекурсии. Компиляторы для языков высокого уровня должны отображать рекурсивно выраженный алгоритм в нерекурсивный. Применяемая при этом техника, несомненно, важна для разработчиков компиляторов, но и для вас, даже если вы и не собираетесь написать компилятор, полезно познакомиться с базисными идеями, как для лучшего понимания рекурсии, так и для осознания потенциальных проблем производительности, связанных с реализацией рекурсии.

Мы рассмотрим некоторые рекурсивные схемы и спросим себя, как, если язык не допускает рекурсию, можно было бы спроектировать нерекурсивную версию, называемую также итеративной, доставляющую те же результаты.

Рекурсивная схема

Рассмотрим рекурсивную процедуру r, содержащую собственный вызов:

r (x: T)
    do
        code_before
        r (y)
        code_after
    end
        

Здесь могло бы быть несколько рекурсивных вызовов, но мы пока рассматриваем только один. Что это означает, если вернуться к взгляду "сверху вниз"?

Наличие рекурсии влечет, что ни начало кода метода, ни его конец не являются тем, на что они претендуют (быть началом и концом).

• Когда выполняется code_before, то это вовсе не означает, что выполнение инициировано вызовом метода клиентом a.r(y) или неквалифицированным вызовом r.(y), – это может быть результатом работы экземпляра r, вызывающего себя рекурсивно.
• Когда code_after завершается, это вовсе не означает завершение истории r: это может быть просто завершение одного рекурсивно вызванного экземпляра. В этом случае следует подвести итоги выполнения последнего вызванного экземпляра r и продолжить выполнение предыдущего экземпляра.

Программы и экземпляры их выполнения

Ключевой новинкой последнего наблюдения является понятие экземпляра (называемого также активацией) программы. Мы знаем, что классы имеют экземпляры – "объекты", создаваемые при выполнении ОО-программы. Теперь подобным образом начнем рассматривать и методы класса.

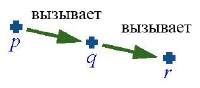
В любой момент выполнения программы состояние вычислений характеризуется цепочкой вызовов, как показано на рисунке. Корневая процедура p вызывает q, которая, в свою очередь, вызывает r… Когда выполнение программы в цепочке завершается, скажем, r, отложенное выполнение вызывающей программы, здесь q, подводит итоги и продолжается с той точки, где оно было прервано при вызове r.

Рис. 9.2. Цепочка вызовов без рекурсии

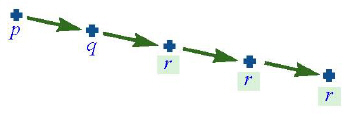
В отсутствие рекурсии не было особой необходимости явного введения понятия экземпляра метода, так как во время выполнения существовал только один активный экземпляр. При рекурсии цепочка вызовов может включать два или более экземпляров одного и того же метода. При прямой рекурсии они будут следовать друг за другом:

Рис. 9.3. Цепочка вызовов при прямой рекурсии

Например, вызов hanoi(2, s, t, o) непосредственно запустит вызов hanoi(1, s, o, t), который вызовет hanoi(0, s, t, o). В этом состоянии будем иметь три экземпляра процедуры в цепочке вызовов.

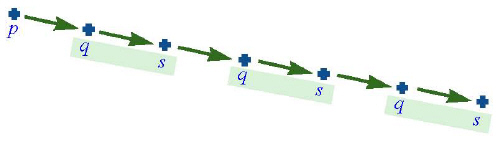
Подобная ситуация существует и при косвенной рекурсии:

Рис. 9.4. Цепочка вызовов при косвенной рекурсии

Сохранение и восстановление контекста

Все экземпляры метода разделяют его код. Экземпляры различаются не кодом, а контекстом выполнения. Мы уже обращали внимание на то, что для правильно построенных рекурсивных методов при каждом вызове контекст экземпляра должен отличаться, по крайней мере, одним элементом от контекста других экземпляров. Контекст, характеризующий экземпляр, включает:

• значения фактических аргументов метода, если они есть, заданные для данного конкретного вызова;
• значения локальных переменных, если они есть;
• точку вызова в тексте вызывающего метода, позволяющую продолжить выполнение после завершения вызванного экземпляра.

При изучении того, как стеки поддерживают выполнение программ в современных языках программирования, мы познакомились со структурой данных, представляющей контекст выполнения метода и называемой записью активации.

При рекурсии каждой активации нужен собственный контекст. Так что остаются только две возможности реализации.

Два подхода не являются исключающими друг друга. Можно использовать подход I2 для элементов контекста, допускающих простую трансформацию, как с аргументом n в методе hanoi(n, …), и создавать запись активации для остальных элементов контекста. Как всегда, решение принимается на основе компромисса "память или время".

Использование явного стека вызова

Из двух рассмотренных стратегий управления контекстом рассмотрим вначале первую, основанную на явных записях активации.

Подобно записям активации, динамически создаются и объекты в результате выполнения оператора create. Память программы, предназначенная для динамического распределения, называется кучей (heap). Но для записей активации нет необходимости использовать кучу, так как образцы активации и деактивации просты и предсказуемы.

• Вызов метода требует создания записи активации.
• По завершении работы метода становится активной запись вызвавшего метода, а о записи активации отработавшего метода можно забыть (она никогда больше не понадобится, так как новому вызову требуется собственная запись).

Рис. 9.5. Цепочка вызовов и соответствующий стек записей активации

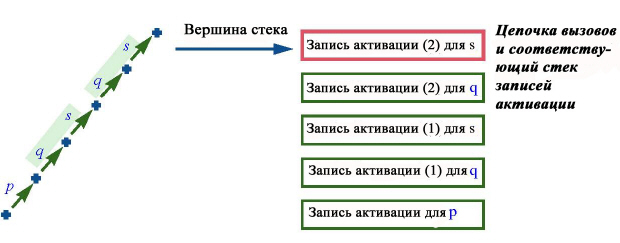
Такая стратегия работы соответствует уже хорошо известной стратегии LIFO "последний пришел – первый ушел", для реализации которой применяется структура данных – стек. Стек записей активации задает цепочку вызовов, что показано на следующем рисунке.

Мы уже ранее встречались со стеком записей активации – он назывался стеком вызовов, сохраняющим историю вызовов методов во время выполнения. Если вы программируете на языке, поддерживающем рекурсию, то создание стека вызовов выполняется компилятором. Сейчас же мы посмотрим, как это можно сделать самому.

Вам может понадобиться явный стек записей активации, если по каким-либо причинам вы захотите написать итеративный вариант рекурсивного метода.

• Для получения доступа к локальным переменным и аргументам метода используйте соответствующие поля записи активации в вершине стека.
• Вместо рекурсивного вызова: создайте новую запись активации, инициализируйте ее значениями аргументов и положением точки вызова, поместите ее в стек и перейдите в начало кода, выполняющего метод.
• Вместо возврата: возвращайтесь, только если стек пуст (нет приостановленных вызовов, ждущих своей очереди); в противном случае восстановите значения аргументов и локальных переменных, удалите использованную запись активации из стека, перейдите к подходящему оператору кода метода в точку, прерванную вызовом только что завершенного метода.

Заметьте, обе трансляционные схемы вызова и возврата требуют оператора goto для перехода в нужную точку кода. Это прекрасно при работе с машинным кодом, но при работе с языком высокого уровня такого перехода стараются избежать, и в языке Eiffel оператора goto просто нет. В этом случае приходится временно написать имитацию goto и промоделировать его подходящими структурными средствами.

Основы исключения рекурсии

Давайте посмотрим, как эта схема работает для тела процедуры hanoi с ее двумя рекурсивными вызовами. Будем использовать стек записей активации, называемый просто stack:

stack: STACK [RECORD]
        

Вспомогательный класс RECORD задает запись активации:

note
    description: "Данные, связанные с экземпляром метода"
class RECORD create
    make
feature — Инициализация полей
    make (n: INTEGER; c: INTEGER; s, t, o: CHARACTER)
            — Инициализация полей записи: count, call, source, target, other.
        do
            count := n ; call := c; source := s ; target := t ; other := o
        end
feature — Access
    count: INTEGER.
            — Число дисков.
    call: INTEGER
            — Идентифицирует рекурсивный вызов: 1 – первый вызов, 2 – второй.
    source, target, other: CHARACTER
        — Стержни.
end
        

(вместо полноценного класса можно было бы использовать кортеж). Экземпляр класса представляет контекст вызова: число перемещаемых дисков (count), три стержня в порядке их использования в вызове, и call, задающее, первый или второй рекурсивный вызов будет применен.

hanoi (n: INTEGER; source, target, other: CHARACTER)
    do
        if n > 0 then
            hanoi (n–1, source, other, target) — Первый вызов
            move (source, target)
            hanoi (n–1, other, target, source) — Второй вызов
        end
    end
        

Мы задействуем стек записей активации для реализации нерекурсивной версии процедуры, временно использующей goto:

iterative_hanoi (n: INTEGER; source, target, other: CHARACTER)
    local — Нам необходимы локальные переменные, представляющие аргументы
            — последовательных вызовов:
        count: INTEGER
        x, y, z, t: CHARACTER
        call: INTEGER
        top: RECORD
    do — Инициализация локальных переменных:
        count := n; x := source; y := target; z := other
start: if count > 0 then
                    — Трансляция hanoi (n–1, source, other, target):
            stack.put (create {RECORD}. make (count, 1, x, y, z))
            count := count – 1
            t := y ; y := z ; z := t
            goto start
after_1: move(x, y )
                    — Трансляция hanoi (n–1, other, target, source):
            stack.put (create{RECORD}.make(count, 2, x, y, z))
            count := count – 1
            t := x ; x := z ; z := t
            goto start
        end
                    — Трансляция возврата:
after_2: if not stack.is_empty then
            top := stack.item – Вершина стека
            count := top.count
            x := top.source ; y := top.target ; z := top.other
            call := top.call ; stack.remove
            if call = 2 then
                goto after_2
            else
                goto after_1
            end
        end
                   — Отсутствует предложение else: программа завершается тогда и
                   — только тогда, когда стек пуст.
    end
        

Тело процедуры iterative_hanoi получено из рекурсивной процедуры hanoi систематическим применением техники исключения рекурсии.

Эта общая схема применима к исключению рекурсии в любой рекурсивной программе, выполняемой как самим программистом в собственных целях, так и разработчиками трансляторов.

Мы теперь рассмотрим возможность ее упрощения, включая удаление goto. Нам понадобится более глубокое понимание структуры программы. В то же время убедитесь, что вы хорошо понимаете этот "грубый" вариант исключения рекурсии.

Рис. 9.6. Питер Наур и Джим Хорнинг (2006)

Почувствуй историю

Говоря о независимом изобретении понятия стека вызовов, Хорнинг, видимо, имеет в виду Фридриха Бауэра из Мюнхена, который использовал термин Keller (cellar), и Эдсгера Дейкстру из Голландии, когда он реализовал свой собственный компилятор Алгола 60.

Рис. 9.7. Фридрих Бауэр (2005)