| Россия |
Приложения ординалов
Лемма. Класс  замкнут
относительно счетных объединений
и пересечений и потому содержит все борелевские множества.
замкнут
относительно счетных объединений
и пересечений и потому содержит все борелевские множества.
Доказательство леммы. Пусть имеется счетная последовательность
множеств  , принадлежащих
, принадлежащих  .
Ординал
.
Ординал 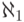 - предельный, и
класс
- предельный, и
класс  является объединением
меньших классов. Поэтому каждое из множеств
является объединением
меньших классов. Поэтому каждое из множеств 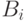 принадлежит
какому- то классу
принадлежит
какому- то классу  , где
, где 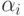 -
некоторый ординал, меньший
-
некоторый ординал, меньший 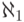 , -е конечный или
счетный ординал. Положим
, -е конечный или
счетный ординал. Положим  .
Ординал
.
Ординал  есть
точная верхняя грань счетного числа счетных
ординалов и потому счетен. В самом деле, рассмотрим
ординалы
есть
точная верхняя грань счетного числа счетных
ординалов и потому счетен. В самом деле, рассмотрим
ординалы 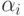 как начальные отрезки в каком- то большем
ординале
(например, в
как начальные отрезки в каком- то большем
ординале
(например, в 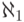 ); их точная верхняя грань будет
объединением счетного числа счетных начальных отрезков и
потому будет счетным ординалом.
); их точная верхняя грань будет
объединением счетного числа счетных начальных отрезков и
потому будет счетным ординалом.
Теперь первое утверждение леммы очевидно: все 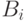 лежат
в
лежат
в 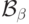 , а потому их объединение (или пересечение)
лежит
в
, а потому их объединение (или пересечение)
лежит
в  и тем более
в
и тем более
в  (поскольку
(поскольку  есть счетный ординал и
меньше
есть счетный ординал и
меньше 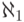 ).
).
Таким образом, класс  является
является  -
алгеброй, содержащей отрезки, и потому содержит все
борелевские множества. Лемма доказана.
-
алгеброй, содержащей отрезки, и потому содержит все
борелевские множества. Лемма доказана.
Как мы уже отмечали, все классы 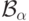 состоят
из борелевских множеств, так что класс
состоят
из борелевских множеств, так что класс  совпадает с классом всех борелевских множеств.
совпадает с классом всех борелевских множеств.
Что можно сказать про мощность классов? Класс 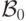 имеет
мощность континуума (отрезки задаются своими концами). Если
класс
имеет
мощность континуума (отрезки задаются своими концами). Если
класс 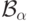 имеет мощность континуума, то и следующий
класс
имеет мощность континуума, то и следующий
класс  имеет мощность континуума (каждый его
элемент задается счетной последовательностью элементов
предшествующего класса,
а
имеет мощность континуума (каждый его
элемент задается счетной последовательностью элементов
предшествующего класса,
а  ).
Каждый предельный класс
есть объединение предыдущих, и пока мы не выходим за пределы
счетных ординалов, объединение это будет счетно,
а
).
Каждый предельный класс
есть объединение предыдущих, и пока мы не выходим за пределы
счетных ординалов, объединение это будет счетно,
а  , так что мы не выходим за
пределы континуума. Наконец,
, так что мы не выходим за
пределы континуума. Наконец,  есть
объединение несчетного числа предыдущих классов (а именно,
есть
объединение несчетного числа предыдущих классов (а именно, 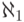 классов), но так как
классов), но так как  ,
то
,
то  .
.
Таким образом, класс  , он же класс всех
борелевских множеств, имеет мощность континуума.
, он же класс всех
борелевских множеств, имеет мощность континуума.
Обычно построение борелевских множеств начинается немного иначе.
Именно, на нижнем уровне рассматриваются два класса: открытые и
замкнутые множества.
На следующем уровне находятся
классы  (счетные объединения
замкнутых множеств)
и
(счетные объединения
замкнутых множеств)
и 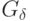 (счетные пересечения
открытых множеств). Еще на
уровень выше лежат счетные пересечения множеств из
(счетные пересечения
открытых множеств). Еще на
уровень выше лежат счетные пересечения множеств из  и
счетные
объединения множеств
из
и
счетные
объединения множеств
из 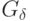 , и т.д. Такой подход является
более естественным
с точки зрения топологии, поскольку отрезки на прямой ничем не
замечательны. Можно проверить, что разница между таким подходом
и нашим определением невелика.
, и т.д. Такой подход является
более естественным
с точки зрения топологии, поскольку отрезки на прямой ничем не
замечательны. Можно проверить, что разница между таким подходом
и нашим определением невелика.
146.Докажите, что пересечение двух  - множеств является
- множеств является  - множеством (и вообще классы
- множеством (и вообще классы  ,
, 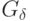 ,
а также классы следующих уровней, замкнуты
относительно конечных объединений и пересечений).
,
а также классы следующих уровней, замкнуты
относительно конечных объединений и пересечений).
147. Докажите, что  - и
- и 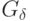 - множества
лежат
в классе
- множества
лежат
в классе  в соответствии с нашей классификацией.
в соответствии с нашей классификацией.
148. Докажите, что всякое множество класса  отличается от
некоторого
отличается от
некоторого  - или
- или 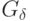 - множества не
более
чем на счетное множество.
- множества не
более
чем на счетное множество.
Докажите, что всякое множество класса  является
счетным пересечением
является
счетным пересечением  - множеств или счетным
объединением
- множеств или счетным
объединением 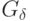 - множеств и что аналогичное утверждение верно
для более высоких уровней нашей иерархии.
- множеств и что аналогичное утверждение верно
для более высоких уровней нашей иерархии.
150.Докажите, что существует открытое множество на плоскости,
среди вертикальных сечений которого встречаются все
открытые подмножества прямой. Докажите, что существует 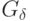 - множество на плоскости, среди сечений которого
встречаются все
- множество на плоскости, среди сечений которого
встречаются все 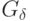 - подмножества прямой.
Докажите аналогичные утверждения для следующих уровней.
- подмножества прямой.
Докажите аналогичные утверждения для следующих уровней.
Покажите, что существует 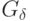 - множество,
не являющееся
- множество,
не являющееся  - множеством. Покажите, что
существует счетное объединение
- множеством. Покажите, что
существует счетное объединение 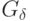 - множеств,
не являющееся счетным пересечением
- множеств,
не являющееся счетным пересечением  - множеств
и т.д. (Указание: воспользуйтесь предыдущей задачей.)
- множеств
и т.д. (Указание: воспользуйтесь предыдущей задачей.)
Ординалы часто появляются при классификации элементов того или иного множества по " рангам". Например, можно классифицировать элементы фундированного множества.
Теорема 45. Пусть  - фундированное множество. Тогда существует и
единственна функция
- фундированное множество. Тогда существует и
единственна функция  , определенная на
, определенная на  и
принимающая
значения в классе ординалов, для которой
и
принимающая
значения в классе ординалов, для которой

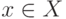 ).
).Доказательство. Определим множество  рекурсией по
ординалу
рекурсией по
ординалу  :
:  состоит из всех элементов
состоит из всех элементов 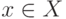 , для
которых
все меньшие их (в
, для
которых
все меньшие их (в  ) элементы принадлежат
) элементы принадлежат  с
меньшими индексами
с
меньшими индексами  :
:

 используется в двух разных смыслах: как порядок на
используется в двух разных смыслах: как порядок на  и как порядок на ординалах.
и как порядок на ординалах.Очевидно, что с ростом  множество
множество  растет
(точнее, не убывает). Докажем, что при достаточно
большом
растет
(точнее, не убывает). Докажем, что при достаточно
большом  множество
множество  покрывает
все
покрывает
все  . Если
это не так, то из
. Если
это не так, то из  следует
следует  (произвольный минимальный элемент, не лежащий
в
(произвольный минимальный элемент, не лежащий
в  ,
принадлежит
,
принадлежит  ). Поэтому отображение
). Поэтому отображение  будет инъекцией, что невозможно (возьмем ординал, по
мощности больший
будет инъекцией, что невозможно (возьмем ординал, по
мощности больший 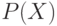 ; предшествующих ему ординалов уже
слишком много).
; предшествующих ему ординалов уже
слишком много).
Теперь определим  как минимальное
как минимальное  ,
при
котором
,
при
котором  . Если
. Если  и
и 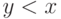 ,
то
,
то  . (В самом деле, по определению
. (В самом деле, по определению  из
из  и
и 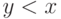 следует,
что
следует,
что  при
некотором
при
некотором 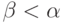 .) Наоборот, если для некоторого
ординала
.) Наоборот, если для некоторого
ординала  выполнено неравенство
выполнено неравенство  при
всех
при
всех 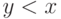 ,
то
,
то  . В самом деле, тогда любой
элемент
. В самом деле, тогда любой
элемент 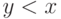 принадлежит
некоторому
принадлежит
некоторому  с
с 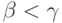 (положим
(положим  )
и потому
)
и потому  и
и  .
.
Итак, построенная нами функция  обладает требуемым
свойством. Единственность доказать совсем легко: если есть
две такие функции, рассмотрим минимальную точку в
обладает требуемым
свойством. Единственность доказать совсем легко: если есть
две такие функции, рассмотрим минимальную точку в  , на которой
они различаются, и сразу же получим противоречие.
, на которой
они различаются, и сразу же получим противоречие.
В частности, счетные ординалы можно использовать для классификации деревьев, в которых нет бесконечных путей. Мы будем рассматривать корневые деревья с конечным или счетным ветвлением (у каждой вершины конечное или счетное число сыновей), в которых нет бесконечной ветви (последовательности вершин, в которых каждая есть сын предыдущей).
Формально такое дерево можно определить как подмножество  множества
множества  конечных
последовательностей натуральных
чисел, замкнутое относительно взятия префикса (если
последовательность принадлежит
конечных
последовательностей натуральных
чисел, замкнутое относительно взятия префикса (если
последовательность принадлежит  , то любой ее начальный
отрезок принадлежит
, то любой ее начальный
отрезок принадлежит  ). Элементы множества
). Элементы множества  мы
называем вершинами дерева; вершина
мы
называем вершинами дерева; вершина  есть сын вершины
есть сын вершины  , если
, если  получается из
получается из  приписыванием справа какого- то
одного
числа. Вершина
приписыванием справа какого- то
одного
числа. Вершина  является потомком вершины
является потомком вершины  ,
если
,
если  получается добавлением к
получается добавлением к  одного или
нескольких
чисел.
одного или
нескольких
чисел.
Мы говорим, что в дереве  нет бесконечной ветви,
если
не существует бесконечной последовательности натуральных чисел,
все начала которой принадлежат
нет бесконечной ветви,
если
не существует бесконечной последовательности натуральных чисел,
все начала которой принадлежат  . В этом случае отношение
порядка
. В этом случае отношение
порядка

 . Ранг его корня
(последовательности длины
. Ранг его корня
(последовательности длины  ) и будем называть рангом
дерева.
) и будем называть рангом
дерева.