| Россия |
Теорема Цермело
Теорема
Аддитивные группы  и
и  изоморфны друг другу.
изоморфны друг другу.
Доказательство.
Рассмотрим  как векторное пространство над
как векторное пространство над  и
выберем базис в этом пространстве. Очевидно, он бесконечен.
Базис в
и
выберем базис в этом пространстве. Очевидно, он бесконечен.
Базис в  может быть
составлен из двух частей, каждая из которых представляет собой
базис в одном из экземпляров
может быть
составлен из двух частей, каждая из которых представляет собой
базис в одном из экземпляров  .
Как мы увидим чуть позже
(
"лекция 11"
), для любого
бесконечного множества
.
Как мы увидим чуть позже
(
"лекция 11"
), для любого
бесконечного множества  удвоенная мощность
удвоенная мощность  (мощность
объединения двух непересекающихся множеств, равномощных
(мощность
объединения двух непересекающихся множеств, равномощных  )
равна мощности
)
равна мощности  .
Наконец, осталось заметить,
что пространства над одним и тем же
полем с равномощными базисами изоморфны как векторные пространства и
тем более как группы.
.
Наконец, осталось заметить,
что пространства над одним и тем же
полем с равномощными базисами изоморфны как векторные пространства и
тем более как группы.
117. Докажите, что любой базис в пространстве  над
полем
над
полем  имеет мощность континуума. (При доказательстве
пригодятся результаты
"лекцию 11"
.)
имеет мощность континуума. (При доказательстве
пригодятся результаты
"лекцию 11"
.)
Мы видели, что трансфинитная индукция позволяет доказать существование базиса в любом векторном пространстве. Продолжая эту линию, можно доказать, что любые два базиса векторного пространства равномощны. (Таким образом, понятие размерности как мощности базиса корректно определено и для бесконечномерных векторных пространств.) Мы вернемся к этому позже (теорема 36).
Отметим, что существование базиса Гамеля можно использовать и quot;в мирных целях", а не только для построения экзотических примеров. Известная " третья проблема Гильберта " состояла в доказательстве того, что многогранники равного объема могут не быть равносоставлены. (Это значит, что один из них нельзя разрезать на меньшие многогранники и сложить из них другой многогранник.) Для многоугольников на плоскости ситуация иная: если два многоугольника равновелики (имеют равную площадь), то они равносоставлены.
Теорема 29. Куб нельзя разрезать на части, из которых можно было бы составить правильный тетраэдр (независимо от объема последнего).
Доказательство. Введем понятие псевдообъема многогранника. Как и объем, псевдообъем будет аддитивен (если многогранник разбит на части, сумма их псевдообъемов равна псевдообъему исходного многогранника); псевдообъемы равных многогранников будут равны. Отсюда следует, что псевдообъемы равносоставленных многогранников будут равны. Мы подберем псевдообъем так, чтобы у куба он равнялся нулю, а у тетраэдра нет - и доказательство будет завершено.
Псевдообъем многогранника мы определим как сумму  , где сумма берется по всем ребрам многогранника,
, где сумма берется по всем ребрам многогранника, 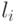 - длина
- длина  -го ребра,
-го ребра, 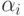 -
двугранный угол при
этом ребре, а
-
двугранный угол при
этом ребре, а  - некоторая функция. Такое определение
автоматически гарантирует, что равные многогранники имеют равные
псевдообъемы. Что нужно от функции
- некоторая функция. Такое определение
автоматически гарантирует, что равные многогранники имеют равные
псевдообъемы. Что нужно от функции  , чтобы псевдообъем был
аддитивен? Представим себе, что многогранник разрезается
плоскостью на две части, и плоскость проходит через уже
имеющееся ребро длины
, чтобы псевдообъем был
аддитивен? Представим себе, что многогранник разрезается
плоскостью на две части, и плоскость проходит через уже
имеющееся ребро длины  . Тогда двугранный
угол
. Тогда двугранный
угол  при этом ребре
разбивается на две части
при этом ребре
разбивается на две части  и
и  . Поэтому в выражении для псевдообъема вместо
слагаемого
. Поэтому в выражении для псевдообъема вместо
слагаемого  появляются
слагаемые
появляются
слагаемые  , и
, и  должно
равняться
должно
равняться  .
Кроме того, разрезающая плоскость может образовать новое ребро,
пересекшись с какой-то гранью. Обозначим длину этого ребра
за
.
Кроме того, разрезающая плоскость может образовать новое ребро,
пересекшись с какой-то гранью. Обозначим длину этого ребра
за  . Тогда в псевдообъеме появятся слагаемые
. Тогда в псевдообъеме появятся слагаемые  (два
образовавшихся двугранных угла дополнительны), которые в сумме должны
равняться нулю.
(два
образовавшихся двугранных угла дополнительны), которые в сумме должны
равняться нулю.
Теперь ясно, какими свойствами должна обладать функция  .
Нужно, чтобы
.
Нужно, чтобы  и
чтобы
и
чтобы  . Тогда псевдообъем будет и впрямь
аддитивен.
Аккуратная проверка требует точного определения понятия
многогранника (что не так и просто), и мы ее проводить не будем. Наглядно
аддитивность
кажется очевидной, особенно если учесть, что все разрезы можно
проводить плоскостями (при этом могут получиться более мелкие
части, но это не страшно).
. Тогда псевдообъем будет и впрямь
аддитивен.
Аккуратная проверка требует точного определения понятия
многогранника (что не так и просто), и мы ее проводить не будем. Наглядно
аддитивность
кажется очевидной, особенно если учесть, что все разрезы можно
проводить плоскостями (при этом могут получиться более мелкие
части, но это не страшно).
Итак, для завершения рассуждения достаточно построить функцию  , для которой
, для которой
-
 для всех
для всех  ;
; -
 (это свойство вместе с предыдущим
гарантирует
аддитивность псевдообъема);
(это свойство вместе с предыдущим
гарантирует
аддитивность псевдообъема); -
 (псевдообъем куба равен нулю; это
свойство,
впрочем, легко следует из двух предыдущих);
(псевдообъем куба равен нулю; это
свойство,
впрочем, легко следует из двух предыдущих); -
 , где
, где  - двугранный
угол при
ребре правильного тетраэдра.
- двугранный
угол при
ребре правильного тетраэдра.
Существенно здесь то, что отношение  иррационально.
Проверим это. Высоты двух соседних граней, опущенные на общее
ребро, образуют равнобедренный треугольник со сторонами
иррационально.
Проверим это. Высоты двух соседних граней, опущенные на общее
ребро, образуют равнобедренный треугольник со сторонами 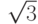 ,
, 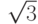 ,
,  ; надо доказать,
что углы этого
треугольника несоизмеримы с
; надо доказать,
что углы этого
треугольника несоизмеримы с  . Удобнее рассмотреть
не
. Удобнее рассмотреть
не  ,
а другой угол треугольника
(два других угла треугольника
равны); обозначим
его
,
а другой угол треугольника
(два других угла треугольника
равны); обозначим
его  . Это угол прямоугольного треугольника со сторонами
. Это угол прямоугольного треугольника со сторонами  ,
, 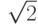 и
и 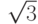 , так что
, так что  . Если бы угол
. Если бы угол  был
соизмерим с
был
соизмерим с  , то и
, то и  был бы соизмерим, поэтому
некоторая степень этого комплексного числа равнялась бы единице.
Можно проверить, однако, что это не так, поскольку кольцо
чисел вида
был бы соизмерим, поэтому
некоторая степень этого комплексного числа равнялась бы единице.
Можно проверить, однако, что это не так, поскольку кольцо
чисел вида  (
(  )
евклидово и
разложение на множители в нем однозначно.
)
евклидово и
разложение на множители в нем однозначно.
Дальнейшее просто: рассмотрим числа  и
и  .
Они
независимы как элементы векторного пространства
.
Они
независимы как элементы векторного пространства  над
над  ,
дополним их до базиса и рассмотрим
,
дополним их до базиса и рассмотрим  -линейный
функционал
-линейный
функционал  , равный коэффициенту
при
, равный коэффициенту
при  в разложении по этому базису. Очевидно, все требования
при этом будут выполнены.
в разложении по этому базису. Очевидно, все требования
при этом будут выполнены.
118. Покажите, что некоторое усложнение этого рассуждения позволяет
обойтись без базиса Гамеля: достаточно определять  не на всех действительных числах, а только на линейных
комбинациях углов, встречающихся при разрезании куба и
тетраэдра на части.
не на всех действительных числах, а только на линейных
комбинациях углов, встречающихся при разрезании куба и
тетраэдра на части.

