| Россия |
Предварительные сведения
Булевы функции от 1-ой и 2-х переменных
Перечислим вначале все булевы функции от 1-ой
переменной  . Как мы знаем, их всего четыре.
. Как мы знаем, их всего четыре.
-
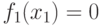 - константа 0;
- константа 0; -
 - константа 1;
- константа 1; -
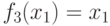 - тождественная функция;
- тождественная функция; -
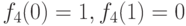 . Эта функция называется отрицанием
. Эта функция называется отрицанием  и обозначается
и обозначается  (используется также обозначение
(используется также обозначение  ,
а в языках программирования эта функция часто обозначается как
,
а в языках программирования эта функция часто обозначается как  ).
).
В следующей таблице представлены наиболее используемые 12 (из 16) функций от 2-х переменных.
 
|
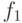 |
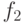 |
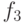 |
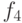 |
 |
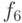 |
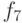 |
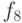 |
 |
 |
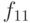 |
 |
|
0 0 0 1 1 0 1 1 |
0 0 0 0 |
1 1 1 1 |
0 0 1 1 |
1 1 0 0 |
0 1 0 1 |
1 0 1 0 |
0 0 0 1 |
0 1 1 1 |
1 1 0 1 |
0 1 1 0 |
1 0 0 1 |
1 1 1 0 |
Многие из этих функций часто считаются "элементарными" и имеют собственные обозначения.
-
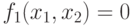 - константа 0;
- константа 0; -
 - константа 1;
- константа 1; -
 - функция, равная 1-му аргументу;
- функция, равная 1-му аргументу; -
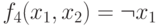 - отрицание
- отрицание  ;
; -
 - функция, равная 2-му аргументу;
- функция, равная 2-му аргументу; -
 - отрицание
- отрицание  ;
; -
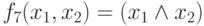 - конъюнкция, читается
"
- конъюнкция, читается
"  и
и  "
(используются также обозначения
"
(используются также обозначения 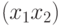 ,
, 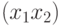 ,
, 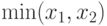 и
и  AND
AND  ));
)); -
 - дизъюнкция, читается
"
- дизъюнкция, читается
"  или
или  "
(используются также обозначения
"
(используются также обозначения  ,
,  и
и  OR
OR  ));
)); -
 - импликация,
читается "
- импликация,
читается "  влечет
влечет  "
или "из
"
или "из  следует
следует  "
(используются также обозначения
"
(используются также обозначения  , и ( IF
, и ( IF  THEN
THEN  ));
)); -
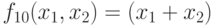 - сложение по модулю 2,
читается "
- сложение по модулю 2,
читается "  плюс
плюс  "
(используется также обозначение
"
(используется также обозначение  );
); -
 - эквивалентность,
читается "
- эквивалентность,
читается "  эквивалентно (равносильно)
эквивалентно (равносильно)  " (используется также обозначение
" (используется также обозначение  );
); -
 - штрих Шеффера (антиконъюнкция),
иногда читается как "не
- штрих Шеффера (антиконъюнкция),
иногда читается как "не  и
и  ".
".
В качестве элементарных функций будем также рассматривать 0-местные функции-константы 0 и 1.
Отметим, что функции  и
и 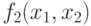 фактически не зависят от значений
обоих аргументов, функции
фактически не зависят от значений
обоих аргументов, функции  и
и  не зависят от значений аргумента
не зависят от значений аргумента  , а функции
, а функции 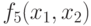 и
и  не зависят от значений аргумента
не зависят от значений аргумента  .
.
Определение 1.1. Функция
не зависит от аргумента
, если для любого набора значений
остальных аргументов
имеет место равенство
Такой аргумент
называется фиктивным. Аргументы, не являющиеся фиктивными, называются существенными.
Функции
и
называются равными, если функцию
можно получить из функции
путем добавления и удаления фиктивных аргументов.
Например, равными являются одноместная функция  и
двухместная функция
и
двухместная функция  , так как вторая получается из первой добавлением фиктивного аргумента
, так как вторая получается из первой добавлением фиктивного аргумента  . Мы не будем различать равные функции и, как правило, будем использовать для обозначения равных функций одно и то же имя функции. В частности, это позволяет считать, что во всяком конечном множестве функций все функции зависят от одного и того же множества переменных.
. Мы не будем различать равные функции и, как правило, будем использовать для обозначения равных функций одно и то же имя функции. В частности, это позволяет считать, что во всяком конечном множестве функций все функции зависят от одного и того же множества переменных.

