|
Хотелось бы иметь возможность читать текст сносок при использовании режима "Версия для печати" |
Базисные средства манипулирования реляционными данными: алгебра A Дейта и Дарвена
Операция реляционной дизъюнкции
Пусть s обозначает результат операции r1 <OR> r2. Для обеспечения возможности выполнения операции требуется, чтобы если 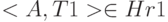 и
и 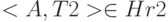 , то должно быть T1 = T2 (одноименные атрибуты должны быть определены на одном и том же типе). Тогда:
, то должно быть T1 = T2 (одноименные атрибуты должны быть определены на одном и том же типе). Тогда:
- Hs = Hr1 union Hr2 (из схемы результата удаляются атрибуты-дубликаты);
-
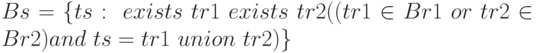 ; очевидно, что при этом:
; очевидно, что при этом:- если у операндов нет общих атрибутов, то в тело результирующего отношения входят все такие кортежи ts, которые являются объединением кортежей tr1 и tr2, соответствующих заголовкам отношений-операндов, и хотя бы один из этих кортежей принадлежит телу одного из операндов;
- если у операндов имеются общие атрибуты, то в тело результирующего отношения входят все такие кортежи ts, которые являются объединением кортежей tr1 и tr2, соответствующих заголовкам отношений-операндов, если хотя бы один из этих кортежей принадлежит телу одного из операндов, и значения общих атрибутов tr1 и tr2 совпадают;
- если же схемы отношений-операндов совпадают, то тело отношения-результата является объединением тел операндов.
Операция <OR> является реляционной дизъюнкцией и обобщением того, что ранее называлось объединением. Заголовок s есть объединение заголовков r1 и r2. Тело s состоит из всех кортежей, соответствующих заголовку s и являющихся надмножеством либо некоторого кортежа из тела r1, либо некоторого кортежа из тела r2.
Предположим, у нас имеются отношения ПРОЕКТЫ_1 {ПРОЕКТ_НАЗВ, ПРОЕКТ_РУК} и НОМЕРА_ПРОЕКТОВ {ПРО_НОМ} (рис. 4.5). Предположим также, что домен атрибута ПРОЕКТ_НАЗВ включает значения ПРОЕКТ_1, ПРОЕКТ_2, ПРОЕКТ_3, домен атрибута ПРОЕКТ_РУК ограничен значениями Иванов, Иваненко, а доменом атрибута ПРО_НОМ является множество {1, 2, 3}. Результат операции ПРОЕКТЫ <OR> НОМЕРА_ПРОЕКТОВ показан на рис. 4.5.
Как показано на рис. 4.5, операция <OR> при наличии операндов с несовпадающими схемами производит результат, гораздо более мощный, чем результат операции взятия расширенного декартова произведения из лекции 3, и еще менее осмысленный с практической точки зрения.
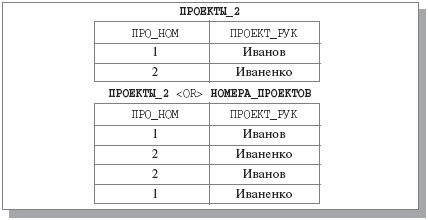
Для иллюстрации операции <OR> над операндами, схемы которых имеют непустое пересечение, воспользуемся отношением ПРОЕКТЫ_2 {ПРО_НОМ, ПРОЕКТ_РУК} (рис. 4.6) и унарным отношением НОМЕРА_ПРОЕКТОВ, схема и тело которого показаны на рис. 4.5. Будем предполагать, что множества значений доменов атрибутов такие же, как в предыдущем примере. Результат операции ПРОЕКТЫ_2 <OR> НОМЕРА_ПРОЕКТОВ показан на рис. 4.6.
Как уже отмечалось, при совпадении схем отношений-операндов результатом выполнения над ними операции <OR> является объединение отношений. Это непосредственно следует из спецификации операции. Если этот факт кажется неочевидным, еще раз внимательно посмотрите на спецификацию. Иллюстрирующий пример мы приводить не будем.