Модификации генетических алгоритмов

3.7. Генетические микроалгоритмы

Данная модификация предназначена для решения задач, которые не требуют популяций с большим числом особей и длинных хромосом. Такой подход оправдан в том случае, когда решение (не обязательно глобальный оптимум) необходимо найти как можно быстрее. В этом случае необходимо уменьшить трудоемкость, связанную с большим количеством итераций, ценой возможно ухудшения качества решения. Такой подход, например, реализован в программе FlexTool [4] следующим генетическим микроалгоритмом.

1. Формирование популяции из 5 особей. При этом можно либо случайным образом выбирать все 5 хромосом, либо сохранять одну "хорошую" особь, полученную на предыдущих итерациях, и случайным образом генерировать остальные 4 особи.
2. Расчет значений фитнесс-функции особей в популяции и выбор лучшей особи. Присвоить ей номер 5 и перенести в следующее поколение (согласно элитарной стратегии).
3. Выбор для репродукции остальных четырех хромосом на основе турнирного метода селекции. При этом хромосомы группируются случайным образом, и соседние пары соперничают за оставшиеся 4 места. Необходимо следить, чтобы родительская пара не формировалась из двух копий одной и той же хромосомы.
4. Выполнение кроссинговера с вероятностью 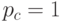(вероятность мутации положить ).
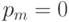5. Проверка сходимости алгоритма (на основе сравнения фенотипов или генотипов). Если условие останова не выполнено, то переход на шаг 2, иначе конец.

Отметим, что в генетическом микроалгоритме используется небольшой фиксированный размер популяции и элитарная стратегия отбора родителей, которая предотвращает потерю хороших особей. Мутация здесь не применяется поскольку разнообразие генетического материала обеспечивается формированием новой популяции при каждом рестарте алгоритма( переходе на шаг 1 при обнаружении сходимости). Процедуры "старта" и "рестарта" предназначены для предотвращения преждевременной сходимости.

3.8. Генетические алгоритмы с изменяемой мощностью популяции

Мощность популяции является важнейшим параметром ГА, который критичен во многих приложениях. Если мало, то ГА работает быстро, но при этом увеличивается опасность преждевременной сходимости к локальному экстремуму. Большая мощность популяции увеличивает генофонд, но процесс поиска замедляется.

На разных этапах работы ГА оптимальное значение может быть различным. На начальном этапе должно быть большим, а на заключительном можно уменьшить.

При одном из подходов в ГА с изменяемым размером популяции каждой особи после ее рождения на текущем этапе оценки целевой функции (ЦФ) присваивается "время жизни" (life time) – параметр, зависящий от ЦФ особи. Таким образом, каждая особь живет определенное число поколений и умирает по окончании срока жизни. Очевидно, значение этого параметра влияет на размер популяции. В этом случае ГА можно реализовать, например, следующим образом [5].

Нестационарный_ГА
{
	t =0;
	Инициализация;
	Оценка ЦФ p(t);
	While (условие окончания не выполнено)
	{
		t=t+1;
		Увеличение возраста каждой особи на 1;
		Рекомбинация p(t):
		Мутация p(t):
		Оценка ЦФ p(t):
		Определение срока жизни особей;
		Удаление из p(t) всех особей с возрастом больше срока жизни;
	} 
}
	

Здесь в текущем поколении алгоритм обрабатывает популяцию . В процессе рекомбинации и мутации генерируется промежуточная популяция, состоящая из потомков, и ее размер пропорционален числу исходной .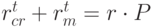

Тогда 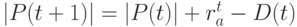– число особей в новой популяции.

Срок жизни для каждой особи определяется после оценки ЦФ (по формулам, приведенным ниже) и является окончательным, то есть постоянным в процессе эволюции. В таком случае особь живет определенное число поколений, а затем умирает. Срок жизни определяет число поколений, в течении которых особь держится в популяции. Очевидно, что в этом случае, чем больше срок жизни, тем больше потомков может дать особь, так как на каждом этапе родители для рекомбинации выбираются случайно с равной вероятностью. При этом подходе важнейшую роль играет метод определения срока жизни особи.

Очевидно, постоянное значение 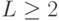для каждой особи ведет к экспоненциальному росту размеров популяции. Поэтому для каждой особи срок жизни вычисляется индивидуально в зависимости от значения ее ЦФ.

Наиболее часто используются следующие три способа определения срока жизни.

Для их определения введем следующие обозначения:

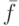• - среднее значение ЦФ по популяции;
• - максимальное значение ЦФ по популяции;
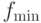• - минимальное значение ЦФ по популяции;
• - абсолютное максимальное значение;
• - абсолютное минимальное значение;
• - максимальный срок жизни;
• - минимальный срок жизни.

1. При пропорциональном методе определения срока жизни

   :

   ( 3.13)

   где (используется для всех формул).
2. При линейном методе определения срока жизни

   ( 3.14)

3. В билинейном методе определения срока жизни

   ( 3.15)

Очевидно, что первый метод соответствует пропорциональному отбору отбора родителей - "рулетке". К минимальному сроку жизни добавляется премиальный срок, который пропорционален значению ЦФ для данной особи. Однако эта стратегия имеет серьезный недостаток – она не учитывает информацию о некоторых объективных характеристиках особи, такой, например, как отношение (или ) целевой функции по популяции.

Эту проблему решает вторая (линейная) стратегия, где срок жизни определяется исходя из значения ЦФ данной особи относительно максимального значения в популяции . Но этот метод тоже имеет свои недостатки - если в популяции много особей имеют значение ЦФ стремящееся к максимальному () значению, то такой подход приведет к чрезмерному увеличению размера популяции.

В третьей стратегии (билинейной) предпринята попытка найти компромисс между первыми двумя методами. В ней учитываются разница между сроками жизни, близкими к лучшей особи, используя информацию о среднем значении популяции. Однако в тоже время принимается во внимание минимальное и максимальное значение по популяции.