| Казахстан |
Параметрические кривые и их растеризация
4.2. Аппроксимация
Кривые Безье
В настоящее время для задач аппроксимации широко применяются кривые Безье (B'ezier) [14]. Это связано с их удобством как для аналитического описания, так и для наглядного геометрического построения (применительно к компьютерной графике это означает, что пользователь может задавать форму кривой интерактивно, т.е. двигая опорные точки курсором на экране).
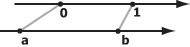
Наглядный метод построения этих кривых был предложен де Кастелье (de Casteljau) в 1959 году [26]. Метод де Кастелье основан на разбиении отрезков, соединяющих исходные точки в отношении t (значение параметра), а затем в рекурсивном повторении этого процесса для полученных отрезков:
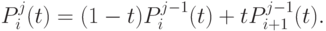 |
( 4.1) |
Нижний индекс - номер точки, верхний индекс - уровень разбиения. Уравнение кривой n -ого порядка задается 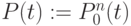 .
.
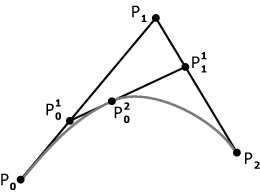
Для примера построим кривую c 3 опорными точками (иногда они также называются контрольными ) (см. рис. 4.2).
Обозначим опорные точки как 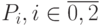 , начало кривой положим в точке
, начало кривой положим в точке 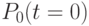 , а конец - в точке
, а конец - в точке 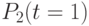 ; для каждого
; для каждого ![t \in [0, 1]](/sites/default/files/tex_cache/a34793831750cd8ae38e3362601907c1.png) найдем точку
найдем точку  :
:
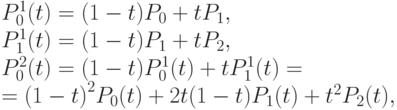
таким образом, получим кривую второго порядка.
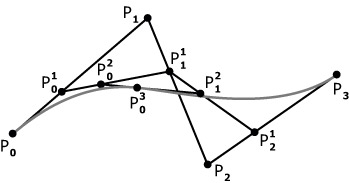
Теперь построим аналогичным методом кривую Безье с четырьмя опорными точками:
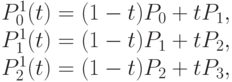
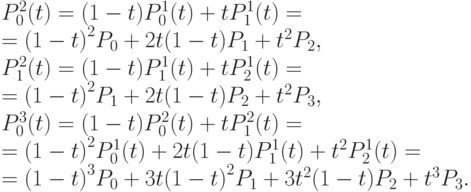
Запишем общее аналитическое представление для кривой Безье с N + 1 опорной точкой:
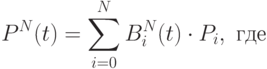 |
( 4.2) |
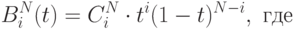

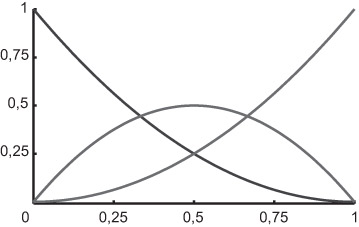
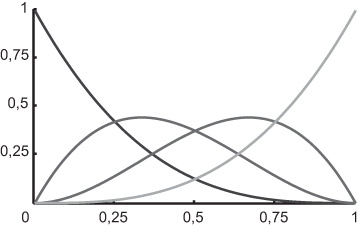
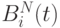 называются базисными многочленами Бернштейна N - й степени (а также весовыми функциями Безье-Бернштейна). На рис. 4.4 и 4.5 изображены многочлены Бернштейна 3-й и 4-й степеней.
называются базисными многочленами Бернштейна N - й степени (а также весовыми функциями Безье-Бернштейна). На рис. 4.4 и 4.5 изображены многочлены Бернштейна 3-й и 4-й степеней.
Свойства кривых Безье
- Инвариантность относительно аффинных преобразований.
- Инвариантность относительно линейных замен параметризации
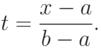
- Кривая Безье принадлежит выпуклой оболочке опорных точек (следует из геометрического способа построения).
Следствие. Если все опорные точки лежат на одной прямой, то кривая Безье вырождается в отрезок, соединяющий эти точки.
- Кривая Безье проходит через P0 и PN.
- Симметричность: если рассматривать контрольные точки в противоположном порядке, то кривая не изменится.
- Степень многочлена, представляющего кривую в аналитическом виде, на 1 меньше числа опорных точек.
- Касательные в точках P0 и PN коллинеарны
 и
и 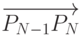 , соответственно.
, соответственно.
Замечание. Хотя все выкладки проводились в  , аналогичные построения и свойства справедливы и в
, аналогичные построения и свойства справедливы и в 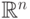 .
.