| Казахстан |
Основные понятия. Представление цвета в машинной графике
1.2. Представление цвета в машинной графике
Понятие цвета возникает при описании восприятия глазами человека электромагнитных волн в определенном диапазоне частот (длина волны  от 400 нм (фиолетовый) до 700 нм (красный) (см. рис. 1.3)). Таким образом, самым общим описанием светового потока может служить его спектральная функция
от 400 нм (фиолетовый) до 700 нм (красный) (см. рис. 1.3)). Таким образом, самым общим описанием светового потока может служить его спектральная функция 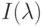 . Свет называется монохроматическим (не путать с монохромными дисплеями, рассматриваемыми в следующей лекции), если его спектр состоит из одного значения
. Свет называется монохроматическим (не путать с монохромными дисплеями, рассматриваемыми в следующей лекции), если его спектр состоит из одного значения  ; математически
; математически 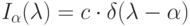 ), где c - яркость. Понятно, что описание цвета путем описания функции в большинстве случаев слишком громоздко, хотя иногда и
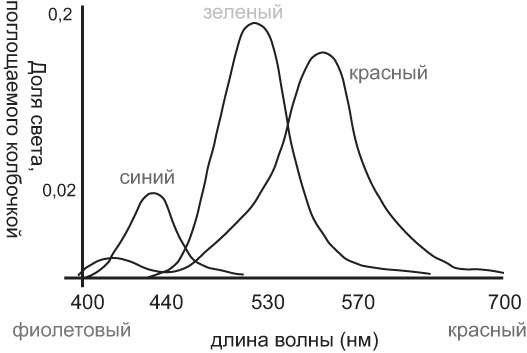
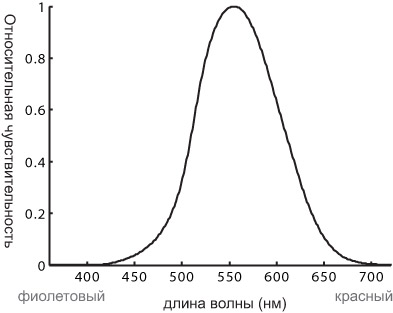
применяется. К тому же, оно является избыточным, если подробнее рассмотреть, как глаз человека воспринимает свет. На сетчатке глаза находятся два типа рецепторов: палочки и колбочки. Палочки реагируют на степень яркости (или интенсивность) падающего света (см. рис. 1.4), а колбочки отвечают за различение цветов; при этом колбочки резко теряют свою чувствительность в темноте (в отличие от палочек), поэтому все объекты начинают казаться серыми. Колбочки бывают трех видов (их часто обозначают S, M и L )2по длине волны - от англ. Small, Middle, Large - малая, средняя и длинная , и их
кривые относительной чувствительности представлены на рис. 1.3. Пики на кривых чувствительности отвечают красному, зеленому и синему цветам. При этом следует заметить, что восприимчивость к синему цвету значительно ниже, чем к двум другим. Также важным свойством восприятия света человеком является его линейность: при освещении двумя источниками света (со спектральными функциями
), где c - яркость. Понятно, что описание цвета путем описания функции в большинстве случаев слишком громоздко, хотя иногда и
применяется. К тому же, оно является избыточным, если подробнее рассмотреть, как глаз человека воспринимает свет. На сетчатке глаза находятся два типа рецепторов: палочки и колбочки. Палочки реагируют на степень яркости (или интенсивность) падающего света (см. рис. 1.4), а колбочки отвечают за различение цветов; при этом колбочки резко теряют свою чувствительность в темноте (в отличие от палочек), поэтому все объекты начинают казаться серыми. Колбочки бывают трех видов (их часто обозначают S, M и L )2по длине волны - от англ. Small, Middle, Large - малая, средняя и длинная , и их
кривые относительной чувствительности представлены на рис. 1.3. Пики на кривых чувствительности отвечают красному, зеленому и синему цветам. При этом следует заметить, что восприимчивость к синему цвету значительно ниже, чем к двум другим. Также важным свойством восприятия света человеком является его линейность: при освещении двумя источниками света (со спектральными функциями 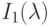 ,
, 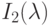 ) человек воспринимает их как один со спектральной функцией, равной сумме
) человек воспринимает их как один со спектральной функцией, равной сумме 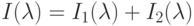 . Этот факт называется законом Грассмана. Благодаря ему можно строить сравнительно простую теорию цветовосприятия.
. Этот факт называется законом Грассмана. Благодаря ему можно строить сравнительно простую теорию цветовосприятия.
Так как области восприятия для разных типов колбочек перекрываются, то возникают метамеры, - потоки волн с разными спектральными характеристиками, но воспринимаемые как имеющие один и тот же цвет.
Цветовая модель RGB
Из рассмотренной выше модели человеческого зрения вытекает, что достаточно обоснованной является цветовая модель RGB (от англ. Red, Green, Blue - красный, зеленый, голубой), в которой спектральная функция представляется как сумма кривых чувствительности для каждого типа колбочек с неотрицательными весовыми коэффициентами (обычно их нормируют от 0 до 1 ), которые так и обозначаются - R, G и B. Эта модель характеризуется свойством аддитивности (мы складываем цвета для получения новых). К примеру, спектральные функции:
- черного цвета: fblack = 0, (R,G,B) = (0,0,0) ;
- фиолетового цвета fviolet = fred + fblue, (R,G,B) = (1,0,1) ;
- белого цвета fwhite = fred + fgreen + fblue, (R,G,B) = (1,1,1).
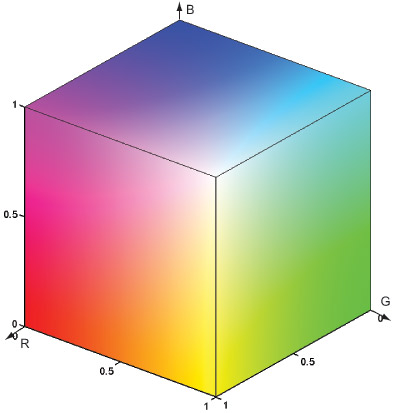
Если представить эти коэффициенты как координаты в трехмерном евклидовом пространстве и каждой точке сопоставить соответствующий цвет, получим наглядное изображение пространства RGB (см. рис. 1.5).
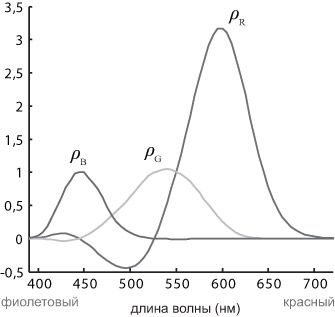
Эта модель является в настоящее время самой распространенной. В то же время ей присущ важный недостаток: не все цвета, видимые человеком, представимы в этой модели. В конце 1920-х годов В.Д. Райтом [53] и Дж. Гилдом [33] были проведены эксперименты, в которых наблюдателю предлагалось каждому монохроматическому цвету3Естественно, образцы брались с определенным шагом по спектру, равным 2 нм. фиксированной яркости в видимом диапазоне сопоставить цвет, составленный из смеси основных цветов R, G и B с некоторыми весами, регулируемыми наблюдателем. Оказалось, что для некоторых цветов необходимо было добавить отдельно яркости испытуемого света и одного из базисных цветов (был выбран R ), с тем чтобы получить одинаковое восприятие. Это соответствует отрицательному весу R -компоненты (см. рис. 1.6). Такой эффект связан с тем, что волны из видимого диапазона воздействуют сразу на все типы колбочек и не всегда возможно ограничиться положительными коэффициентами (более подробно см. [24]) для представления некоторых цветов из видимого спектра. К счастью, доля воспроизводимых цветов значительно больше, чем доля не представимых в этой модели цветов. Модель, с помощью которой можно представить все цвета из спектра, ограничиваясь неотрицательными коэффициентами, представлена в следующем подразделе.