| Россия |
Алгоритмы проектирования проводных и печатных соединений (методы трассировки)
Основное назначение лекции - показать работу алгоритмов трассировки на конкретных примерах для лучшего усвоения материала.
21.1. Постановка задачи. Разновидности задач трассировки
Трассировка монтажных соединений - это задача геометрического построения на КП всех цепей данной конструкции, координаты начала и конца которых определены при размещении элементов. Следовательно, задача трассировки состоит в отыскании геометрически определенного способа соединений эквипотенциальных выводов схемы.
При этом необходимо учитывать различные конструктивно-технические ограничения: допускаются пересечения или нет, возможен ли переход с одного слоя на другой, сколько слоев отводится для трассировки, допустимые ширина проводников и расстояния между ними и т. д.
Алгоритмы трассировки существенно зависят от принятой конструкции и технологии изготовления РЭС.
Задачи трассировки можно разделить на две группы: трассировка проводных соединений и трассировка печатных (пленочных) соединений.
Трассировка проводных соединений в целом относительно более проста, поскольку отдельные сигнальные цепи электрически изолированы друг от друга. Поэтому в большинстве случаев она может быть сведена к оптимизации трасс соединений отдельных цепей. Наиболее распространенный подход к оптимизации трасс проводных соединений основан на использовании алгоритмов построения минимальных связывающих деревьев. Но и при проводном монтаже возникают проблемы совместной оптимизации соединений монтажных схем, определяемые такими факторами, как, например, электромагнитная совместимость проводов, наличие жгутов заданной формы и размера и другие. В подобных ситуациях задачи трассировки проводных соединений становятся по сложности и постановке близкими к задачам трассировки печатного монтажа.
Трассировка печатных и пленочных соединений непосредственно связана с согласованием метрических и топологических параметров схемы соединений и соответствующих параметров коммутационного поля (КП).
К метрическим параметрам схемы можно отнести размеры элементов, ширину проводников и допустимые расстояния между ними, предельно допустимые длины соединений и т. д.
Топологические параметры схемы определяются такими ее структурными свойствами, как планарность, т. е. возможность расположения на плоскости без пересечений, минимальное число пересечений и другие. Топологические параметры коммутационного поля КП определяются принятыми конструктивными способами устранения пересечений.
21.2. Общая характеристика методов трассировки
Проектирование схем соединений, иначе трассировка соединений, является одной из наиболее трудных задач в общей проблеме автоматизации проектирования электронных устройств. Прежде всего, это связано с многообразием способов конструктивно-технологической реализации соединений, каждый из которых обуславливает использование специфических критериев оптимизации при алгоритмическом решении задачи трассировки.
Исходной информацией для решения задач трассировки соединений являются список цепей, параметры конструкции элементов и коммутационного поля, а также данные по размещению элементов. Перед трассировкой соединений для каждой цепи схемы могут быть рассчитаны координаты расположения выводов на КП.
При алгоритмическом решении задача трассировки состоит в построении для всех цепей схемы оптимальных монтажных соединений.
Как уже отмечалось, задача трассировки имеет метрический и топологический аспекты.
Метрический аспект предполагает учет конструктивных размеров элементов, соединений и КП.
Топологический аспект связан с выбором допустимого пространственного расположения отдельных монтажных соединений на КП при ограничениях на число пересечений соединений, число слоев коммутационной схемы.
Алгоритмические методы проводных и печатных соединений существенно различаются.
Для проводного монтажа трассировка осуществляется с помощью алгоритмов построения минимальных деревьев соединений. Полная монтажная схема (таблица проводов) получается при последовательном применении указанных алгоритмов для отдельных цепей схемы. Далее, на основании анализа паразитных связей, в полученной монтажной схеме трассы отдельных соединений могут быть скорректированы.
Алгоритмические методы трассировки печатных (пленочных) соединений зависят от конструкции коммутационного поля и могут быть разделены на две основные группы.
К первой группе относятся так называемые топографические методы, в которых приоритет отдается метрическому аспекту задачи.
Вторая группа основана на графо-метрическом подходе задачи трассировки.
Для трассировки соединений предложено много алгоритмов, отличающихся скоростью и требуемым объемом памяти при реализации его на ЭВМ, а также качеством результата: волновой алгоритм и его модификации, алгоритмы трассировки по магистралям и каналам и ряд комбинированных алгоритмов. Эффективность применения каждого из них определяется рядом факторов: конструкцией коммутационного поля, ресурсами машинного времени и памяти ЭВМ, сложностью схемы соединений.
Для ряда конструкций электронных устройств разделение общей задачи проектирования топологии на два этапа - размещение элементов и трассировку соединений - не оправдано. Характерными особенностями таких конструкций являются нерегулярность расположения элементов и соединений, их разнотипность, наличие одного слоя коммутации.
Примерами могут служить односторонние печатные платы с микросхемами и навесными радиодеталями в устройствах аналогового типа, гибридные микросхемы и биполярные ИС с одним слоем коммутации. Основным критерием при разработке топологии таких схем является минимум числа пересечений соединений, а ограничением - площадь, занимаемая схемой.
В последнее время проводятся интенсивные исследования по применению графо-теоретических методов к проектированию топологии схем подобного рода, поскольку последовательные топографические методы трассировки в этом случае мало эффективны.
Графо-теоретические методы трассировки предполагают предварительный анализ планарности схемы, представленной в виде графа, и последующую ликвидацию пересечений с помощью технологических приемов. Окончательная фаза состоит в построении эскиза топологии схемы при рациональном распределении функции между конструктором и ЭВМ.
21.3. Трассировка проводных соединений
Монтажные соединения для цепей схемы представляют собой деревья.
Виды используемых деревьев определяются технологией выполнения соединений и схемотехническими требованиями. При автоматизированном конструировании схем проводного и печатного монтажа возникает задача построения минимальных деревьев соединений. Как правило, минимизации подлежит суммарная длина рёбер дерева.
Могут быть использованы и другие критерии оптимизации.
Задача построения минимального дерева формулируется следующим образом.
Пусть, 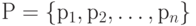 - множество точек плоскости, соответствующих выводам произвольной цепи.
- множество точек плоскости, соответствующих выводам произвольной цепи.
Рассмотрим полный граф 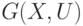 , вершины которого
, вершины которого 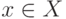 соответствуют выводам цепи, а рёбра u U с приписанным к ним весом
соответствуют выводам цепи, а рёбра u U с приписанным к ним весом  характеризуют соединения между парами выводов. Значение
характеризуют соединения между парами выводов. Значение  может быть равно расстоянию между соответствующими точками множества
может быть равно расстоянию между соответствующими точками множества  . В общем случае
. В общем случае  может представлять линейную комбинацию нескольких характеристик соединения:
может представлять линейную комбинацию нескольких характеристик соединения:
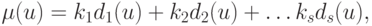 |
( 21.1) |
где 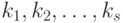 - коэффициенты;
- коэффициенты; 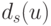 - некоторая характеристика соединения
- некоторая характеристика соединения  .
.
Теперь исходная задача сводится к определению в графе  дерева, включающего все вершины
дерева, включающего все вершины  и имеющего минимальный вес рёбер.
и имеющего минимальный вес рёбер.
Такое дерево называется минимальным покрывающим деревом или минимальным связывающим деревом.
Наиболее эффективен с точки зрения реализации на ЭВМ алгоритм Прима, предполагающий последовательное выполнение следующих принципов:
- всякая изолированная вершина соединяется с ближайшей;
- всякий изолированный фрагмент (связанная группа вершин) соединяется с ближайшей вершиной кратчайшим ребром.
Здесь под расстоянием между вершинами понимают значение  , приписанное рёбрам соответствующего графа. Расстоянием вершины от данного изолированного фрагмента является минимум его расстояний до отдельных вершин фрагмента.
, приписанное рёбрам соответствующего графа. Расстоянием вершины от данного изолированного фрагмента является минимум его расстояний до отдельных вершин фрагмента.
На рис. 21.1 расстоянием вершины 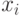 от фрагмента
от фрагмента 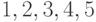 является длина ребра
является длина ребра 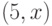 .
.
Алгоритм построения минимального связывающего дерева для цепи с "n" выводами теперь может быть описан следующим образом:
- для произвольного вывода цепи найти ближайший и провести соединение;
- на каждом последующем шаге
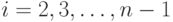 из множества неподсоединённых выводов выбрать тот, который находится ближе остальных (в указанном выше смысле) к группе уже связанных выводов, и подсоединить его к этой группе по кратчайшему пути.
из множества неподсоединённых выводов выбрать тот, который находится ближе остальных (в указанном выше смысле) к группе уже связанных выводов, и подсоединить его к этой группе по кратчайшему пути.
Построенное таким образом дерево будет иметь минимальную суммарную длину соединений.
Иногда при построении связывающего дерева в качестве значения  принимают суммарную оценку,
включающую как длину ребра
принимают суммарную оценку,
включающую как длину ребра 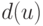 , так и число пересечений
, так и число пересечений 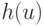 этого ребра с рёбрами уже построенных деревьев
этого ребра с рёбрами уже построенных деревьев
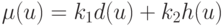 |
( 21.2) |
В частности, такая оценка используется при построении связывающих деревьев для схем печатного монтажа. В этом случае процедура Прима остаётся без изменений, а расстояние между выводами цепи рассчитывается по (21.2).
Построение минимального дерева с ограничением на степени вершин может быть осуществлено при использовании процедур, основанных на методе ветвей и границ. Однако для практических целей предпочтение следует отдавать эвристическим алгоритмам.
В частности, можно использовать модифицированные принципы Прима:
- всякая изолированная вершина соединяется с ближайшей, не соединенной с
 другими вершинами;
другими вершинами; - всякий изолированный фрагмент соединяется кратчайшим ребром с ближайшей вершиной, не соединённой с
 другими вершинами.
другими вершинами.
Приведённые в литературе исследования показывают, что алгоритм, построенный на основании этих принципов, приводит к получению деревьев с длиной, превышающей минимальную не более чем на 5% при числе выводов  .
.
Модифицированные принципы Прима используются иногда при параллельном наращивании нескольких фрагментов дерева. На основании проведённой серии экспериментов (  ) авторы приходят к выводу, что такой способ даёт деревья с меньшей длиной соединений последовательного наращивания одного изолированного фрагмента.
) авторы приходят к выводу, что такой способ даёт деревья с меньшей длиной соединений последовательного наращивания одного изолированного фрагмента.
В некоторых случаях, помимо ограничения на степени вершин связывающего дерева, задаётся начальная и конечная точка цепи.
Например, это имеет место при разработке монтажных схем для высокочастотных цепей, когда необходимо связать в определённой последовательности источник сигнала и несколько нагрузок. Тогда задача сводится к построению кратчайшего пути между двумя заданными выводами, проходящего через все остальные выводы цепи.
Данная задача родственна задаче о маршруте коммивояжера, но отличается от последней тем, что путь обхода должен быть разомкнутым и соединять две заданные точки. Следуя терминологии теории графов, возникает задача построения кратчайшей гамильтоновой цепи между заданными начальной и конечной вершинами.
Рассмотрим алгоритм, дающий приближённое решение этой задачи. Основу алгоритма составляет 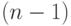 - шаговый процесс:
- шаговый процесс:
- выбора кратчайших рёбер в полном графе
 ;
; - проверки каждого ребра на выполнение ограничений задачи;
- составление из выбранных рёбер пути, соединяющего заданные точки.
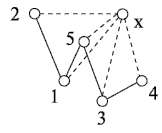
Пусть, задано расположение точек (рис. 21.2)
Здесь  и
и  - соответственно, начальная и конечная точка пути.
- соответственно, начальная и конечная точка пути.
Составим упорядоченную по возрастанию длин последовательность рёбер полного графа 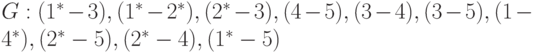 .
.
Очередное ребро  выбирается по порядку из этой последовательности при выполнении условий:
выбирается по порядку из этой последовательности при выполнении условий:
-
ребро не соединяет заданные конечную и начальную точки (
 и
и 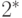 );
); - при включении ребра в путь степень вершин, соединяемых этим ребром, не превышает допустимой (
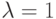 для начальной и конечной точек и
для начальной и конечной точек и 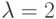 для остальных точек);
для остальных точек); - ребро не образует цикла с рёбрами, уже включенными в путь;
- при включении в путь любого ребра, кроме
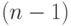 -го, начальная и конечная точки остаются несвязанными.
-го, начальная и конечная точки остаются несвязанными.
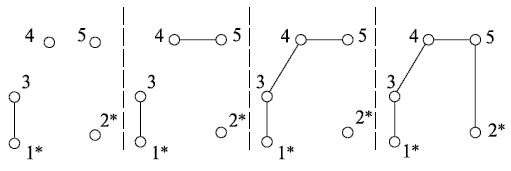
Условия 1 - 3 непосредственно вытекают из ограничений задачи. Условие 4 препятствует образованию тупиковых ситуаций, т.е. такого положения, при котором дальнейшее формирование пути становится невозможным - все подсоединенные точки, кроме начальной и конечной, имеют степень 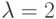 . Пошаговый процесс формирования пути изображен на рис. 20.2, а - г.
. Пошаговый процесс формирования пути изображен на рис. 20.2, а - г.
Шаг 1. Выбираем ребро 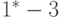 , т.к. оно удовлетворяет всем условиям (рис. 21.2, а).
, т.к. оно удовлетворяет всем условиям (рис. 21.2, а).
Шаг 2. Ребро 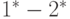 } отбрасывается, т.к. не удовлетворяется условие 1, а ребро
} отбрасывается, т.к. не удовлетворяется условие 1, а ребро  - т.к. не удовлетворяется условие 4. Выбирается ребро 4-5 (рис. 21.2, б).
- т.к. не удовлетворяется условие 4. Выбирается ребро 4-5 (рис. 21.2, б).
Шаг 3. Выбирается ребро 3-4 (рис. 21.2, в).
Шаг 4. Ребра 3-5 и  -4 отбрасываются из-за невыполнения условия 3. Выбирается ребро
-4 отбрасываются из-за невыполнения условия 3. Выбирается ребро  .
Результирующий путь
.
Результирующий путь 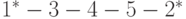 показан на (рис. 21.2,г).
показан на (рис. 21.2,г).
Если снять ограничение о крайних точках пути, то данный алгоритм приводит к более короткому пути 2 - 1 - 3 - 4 - 5. В этом случае алгоритм становится частным случаем модифицированного алгоритма Прима.
Как показано в специальной литературе, использование описанных выше процедур для построения связывающих деревьев с ограниченной степенью вершин обеспечивает вполне приемлемые результаты.