| Россия |
Размещение элементов электрической схемы
Выбор позиции
Выбранный для размещения элемент 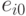 должен быть установлен в одну из незанятых позиций из множества
должен быть установлен в одну из незанятых позиций из множества 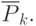 Эта позиция выбирается с учётом минимизации критерия размещения,
в частности МСВД соединений.
При последовательном процессе размещения может быть оценена лишь суммарная длина частичных монтажных соединений данного элемента e _{i 0} с уже размещёнными элементами
Эта позиция выбирается с учётом минимизации критерия размещения,
в частности МСВД соединений.
При последовательном процессе размещения может быть оценена лишь суммарная длина частичных монтажных соединений данного элемента e _{i 0} с уже размещёнными элементами 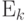 .
.
При установке элемента в позицию рассчитываются трассы соответствующих соединений. Длина этих соединений является критерием для выбора позиций. Однако большие затраты машинного времени делают этот подход нереальным, при конструировании узлов с печатными соединениями, и ограниченно применимым при конструировании монтажных схем проводных соединений.
Для выбора позиции  применяют приближённые методы оценки кратчайших монтажных соединений, т.е. рассчитывают псевдодлину реальных соединений. Одна из них, имеет вид:
применяют приближённые методы оценки кратчайших монтажных соединений, т.е. рассчитывают псевдодлину реальных соединений. Одна из них, имеет вид:
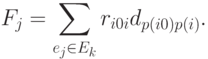 |
( 20.10) |
Выбирается та из позиций, для которой 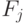 минимальна.
минимальна.
Для экономии вычислений всегда целесообразно рассматривать не всё множество позиций 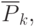 а лишь часть.
а лишь часть.
Эти позиции находятся на периферии множества незанятых позиций 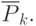
Другой способ выбора позиции состоит в следующем.
Пусть 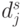 - минимальное расстояние позиции
- минимальное расстояние позиции 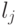 до одного из уже размещенных элементов в цепи
до одного из уже размещенных элементов в цепи 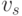 , связанной с элементом
, связанной с элементом 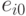 .
Для размещения элемента
.
Для размещения элемента 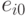 выбирают ту позицию, для которой
выбирают ту позицию, для которой
 |
( 20.11) |
минимальна,  - множество цепей,
связывающих
- множество цепей,
связывающих 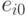 и
и 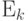 .
.
Поскольку назначение первого элемента предопределяет весь дальнейший процесс размещения, при небольших затратах ЭВМ - времени на реализацию алгоритма, желательно рассмотреть несколько вариантов таких назначений и из полученных размещений выбрать лучшее.
Продолжим расчёты для нашего примера.
Шаг между двумя позициями принимаем равным единице. Пусть, например, 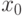 находится в четвёртой позиции. Имеем первоначальное размещение:
находится в четвёртой позиции. Имеем первоначальное размещение: 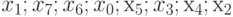 .
.
Первый шаг. Размещаем элемент 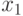 .
Поместим его в каждую из позиций и определим длину:
.
Поместим его в каждую из позиций и определим длину:

Минимальными являются критерии 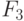 и
и 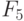 , следовательно, элемент
, следовательно, элемент 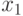 можно разместить в пятой позиции, например:
можно разместить в пятой позиции, например: 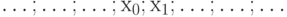 .
.
Второй шаг. Размещаем 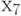 , но с учетом уже двух занятых позиций:
, но с учетом уже двух занятых позиций:
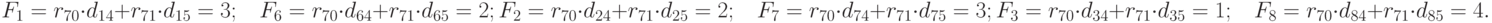
Поскольку минимальным является критерий 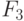 , следовательно,
элемент
, следовательно,
элемент 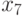 размещаем в третьей позиции.
размещаем в третьей позиции.
Третий шаг. Размещаем 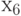 в незанятые позиции:
в незанятые позиции:
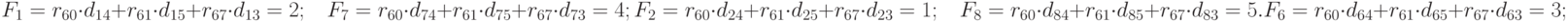
Четвертый шаг. Размещаем  в незанятые позиции:
в незанятые позиции:
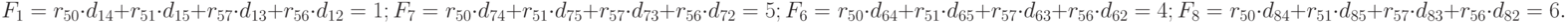
Пятый шаг. Размещаем 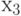 в оставшиеся позиции:
в оставшиеся позиции:
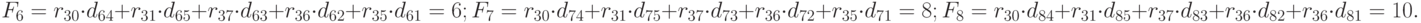
Шестой шаг. Размещаем 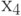 :
:
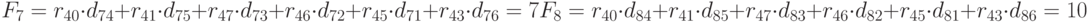
Оставшийся элемент 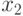 разместим на восьмой позиции.
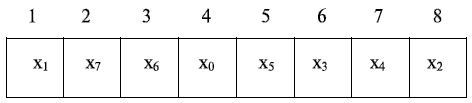
В результате получим следующее размещение элементов:
разместим на восьмой позиции.
В результате получим следующее размещение элементов:
Рассчитаем минимальную суммарную взвешенную длину связей между позициями по формуле
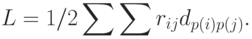
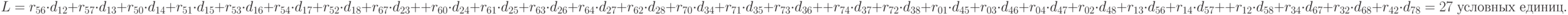
Для оптимизации критерия размещения используются итерационные алгоритмы.

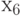 во 2-ю
во 2-ю 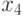 в 7-ю
в 7-ю