Машина вывода Пролога

2.3. Устройство вычислений в Прологе

Для того чтобы проследить за устройством вычислений в программе на языке Пролог возьмем следующий пример.

родитель("Иван", "Мария").
родитель("Анна", "Мария").
родитель("Мария", "Павел").
родитель("Мария", "Петр").

женщина("Мария").
женщина("Анна").

мать(X, Y):- женщина(X), родитель(X, Y).

Рассмотрим процесс поиска решений для цели

мать(X, Y).

Переменные X и Y в этой цели свободны, они не имеют значений при вызове предиката. Свободная переменная унифицируется с любым термом. Решением называется набор значений переменных.

С декларативной точки зрения, нужно найти все пары значений переменных, которые принадлежат бинарному отношению мать/2. Результат имеет вид:

X = Мария, Y = Павел
X = Мария, Y = Петр
X = Анна, Y = Мария

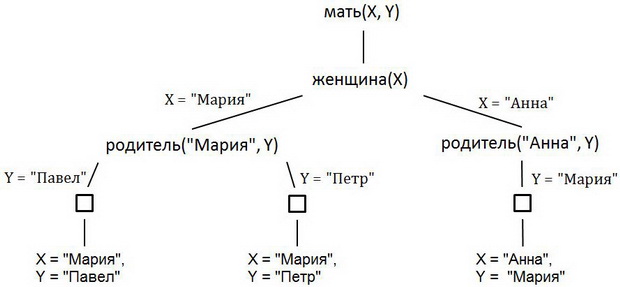
Когда программа приступает к вычислению ответа на запрос, она просматривает все предложения программы сверху вниз и находит первое из них, с заголовком которого унифицируется первая подцель. Переменные правила автоматически переименовываются, так чтобы среди них не было переменных запроса.

Первое правило, с заголовком которого унифицируется цель, имеет вид:

мать(X1, Y1):- женщина(X1), родитель(X1, Y1).

Атомарные формулы мать(X, Y) и мать(X1, Y1) унифицирует подстановка X1 = X, Y1 = Y.

Вычисления соответствуют принципу: заголовок правила истинен, если истинно его тело. Исходная простая цель заменяется последовательностью подцелей из тела правила. Новая цель имеет вид:

женщина(X), родитель(X, Y).

Это цель составная, конъюнктивная. В конъюнктивном запросе переменные с одинаковым именем должны получить одно и то же значение. Сначала вызывается первая подцель:

женщина(X).

При вызове каждой простой цели программа заново просматривает все предложения сверху вниз и ищет такие, с заголовками которых унифицируется текущая цель. Первое из этих правил (с пустым телом) имеет вид:

женщина("Мария").

Возле этого правила ставится точка возврата, для того чтобы при вычислении других вариантов ответа поиск вести с указанного места. Переменная X принимает значение, т. е. конкретизируется значением "Мария" (X = Мария), и это значение передается во вторую подцель, так что новая цель имеет вид:

родитель("Мария", Y).

Правила снова просматриваются сверху вниз, и цель унифицируется с заголовком правила

родитель("Мария", "Павел").

При этом Y = Павел. Возле этого правила также ставится точка возврата.

Тело правила при X = Мария, Y = Павел истинно, поэтому и заголовок мать(X, Y) истинен. В общем случае решение является композицией подстановок, ограниченной переменными цели. Итак, первое решение имеет вид:

X = Мария, Y = Павел.

Теперь делается откат к точке возврата, поставленной последней. При этом переменная Y освобождается от своего значения, а точка возврата удаляется. Цель

родитель("Мария", Y)

унифицируется с заголовком следующего правила (Y = Петр):

родитель("Мария", "Петр").

Само правило помечается точкой возврата. Найдено еще одно решение:

X = Мария, Y = Петр

Делается откат к последней точке возврата, при этом переменная Y освобождается от своего значения. Больше правил нет, поэтому эта точка возврата просто удаляется. Теперь идет откат к предыдущей цели, поиск решений для которой начинается с оставшейся точки возврата, при этом переменная X освобождается от своего значения, а точка возврата удаляется. Цель снова принимает вид:

женщина(X), родитель(X, Y).

Подцель

женщина(X)

унифицируется с заголовком следующего правила (X = Анна):

женщина("Анна").

Возле правила ставится точка возврата. Новая цель имеет вид:

родитель("Анна", Y).

Она унифицируется с заголовком правила (Y = Мария):

родитель("Анна", "Мария").

Возле этого правила также ставится точка возврата. Находится еще одно решение:

X = Анна, Y = Мария

Откат к последней точке возврата приводит только к ее удалению, то же самое происходит с предыдущей точкой возврата. Других решений нет.

Процедура вычислений в языке Пролог моделируется в виде дерева поиска (рис. 2.2). Вершины дерева соответствуют простым целям, а ребра — унифицирующим подстановкам. В дереве мы указали также решения — композиции подстановок. Процедура вычислений соответствует обходу дерева в глубину.

Рис. 2.2. Дерево поиска для цели мать(X, Y)

Рассмотрим пример поиска решений для дизъюнктивной цели.

мужчина("Иван").
мужчина("Павел").
мужчина("Петр").

женщина("Мария").
женщина("Анна").

При поиске решений для дизъюнктивной цели:

женщина(X); мужчина(X).

сначала находятся решения до знака дизъюнкции, а потом после него. Переменные, разделенные знаками дизъюнкции, между собой не связаны. Поэтому решение имеет вид:

X = Мария
X = Анна
X = Иван
X = Павел
X = Петр

Если цель имеет несколько знаков дизъюнкции, то сначала находятся решения до первого знака, потом до второго, и т. д.

Итак, машина вывода Пролога использует для доказательства цели поиск в глубину. Цели доказываются всеми возможными способами, т. е. находятся все решения. Если цель не имеет переменных, то проверяется ее истинность или ложность. Если цель имеет решение, то говорят, что она успешна. Если цель не имеет решений, то она неуспешна. Цель без переменных успешна, если она истинна, и неуспешна в противном случае. Например, вызов предиката fail всегда неуспешный, так как этот предикат имеет значение ложь. С помощью него обычно создается "искусственный" неуспех. В противоположность этому цель succeed() всегда успешна, предикат succeed имеет значение истина. При неуспехе очередной цели Пролог откатывается назад, чтобы найти другие решения, до тех пор пока это возможно. Когда все точки возврата становятся удаленными, и новых целей нет, вычисления заканчиваются.

Переменные, имеющие значение, называют конкретизированными. Остальные переменные называют неконкретизированными. Если аргумент предиката при вызове этого предиката уже имеет значение, то такой аргумент называется входным аргументом, а если не имеет, то выходным аргументом.