Обнаружение коллизий

Обнаружение коллизий по принципу "фильм-фильм" по расстоянию

Это последний метод обнаружения коллизий, который мы рассмотрим. Он полностью подходит для идеально круглых объектов, хотя можно немного схитрить и применить его к тем объектам, которые имеют более-менее округлую форму.

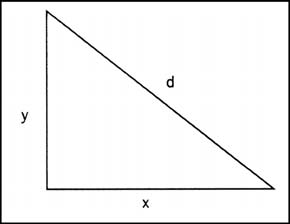
Ранее мы говорили о том, что если два объекта находятся примерно на одной позиции, можно считать, что они находятся в состоянии столкновения. Иными словами, расстояние между двумя объектами равно нулю. Создадим два круглых фильма и будем вычислять расстояние между ними. Для этого мы применим теорему Пифагора. Теорема гласит, что сумма квадратов двух меньших сторон прямоугольного треугольника равна квадрату большей стороны треугольника. Смотрите.

Я пометил стороны буквами x, y и d. Теорема Пифагора гласит.

x2 + y2 = d2

Т.е.:

x*x + y*y = d*d

Теперь, если провести некоторые элементарные алгебраические преобразования, получим следующее.

d = Math.sqrt (x*x + y*y);

Это значит, что если возвести в квадрат обе стороны, сложить их и затем извлечь квадратный корень, получим длину гипотенузы. Теперь немного изменим наш рисунок, и вам все станет ясно.

На рисунке показано, что dx - это расстояние по оси x между mc1_mc и mc2_mc. dy - это расстояние по оси y, а dist - это среднее расстояние между ними. Зная все это, можно интерпретировать данные выводы следующим образом с помощью обычного кода.

dx = mc2_mc._x-mc1_mc._x;
  dy = mc2_mc._y-mc1_mc._y;
  dist = Math.sqrt (dx*dx+dy*dy);

Это еще одна шпаргалка для вас. Запишите эти выражения, они вам пригодятся.

Ранее я говорил, что когда расстояние между двумя фильмами обращается в ноль, объекты сталкиваются. Однако вспомните последнее упражнение с игрой в пинг-понг, где нужно было учитывать размер шарика. Теперь нам нужно брать в расчет размеры обоих фильмов. В нашем случае на данном этапе расстояние между фильмами в 0 пикселей означало бы полное совмещение центров двух шариков, и только в этом случае было бы зарегистрировано столкновение. Это уж слишком!

В последний раз мы просто брали радиус шарика для определения его состояния столкновения. Здесь мы сделаем то же самое, однако вычислим радиус одного шарика и прибавим к нему радиус другого. Если расстояние между шариками будет меньше, чем эта величина, будет регистрироваться столкновение. Красота этого метода состоит в том, что не имеет значения размер фильмов, так как мы будем определять радиусы динамически.

Приведем код для выяснения того, произошло столкновение или нет.

dx=mc2_mc._x-mc1_mc._x;
  dy=mc2_mc._y-mc1_mc._y;
  dist=Math.sqrt(dx*dx+dy*dy);
  if (dist<mc1_mc._width/2 + mc2_mc._width/2){
    // you have a hit!
  }

То, что будет происходить после обнаружения столкновения - уже другая история. Так и хочется создать файл с некоторым количеством сфер, летающих и сталкивающихся друг с другом. Изучив материал до этого момента, становится понятно, что нужно научиться обращать скорости x или y, а это и будет главным "фокусом". К сожалению, все не так просто. Мы рассмотрим некоторые из таких моментов в следующей лекции. А сейчас просто создадим небольшой файл в качестве примера, чтобы вы сами убедились в реальности применения рассмотренного материала.

Это будет еще одна небольшая игра, что-то наподобие Atari's Asteroids, однако вы можете превратить эту игру во все, что придет вам в голову.