|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Задачи оптимизации при принятии решений
Задачи по оптимизационным методам принятия решений
1. Изобразите на плоскости ограничения задачи линейного программирования и решите (графически) эту задачу:
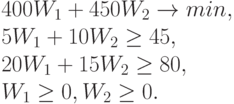
2. Решите задачу линейного программирования:
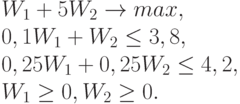
3. Решите задачу целочисленного программирования:
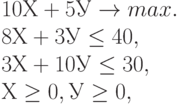
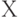 и
и 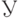 - целые числа.
- целые числа.
4. Решите задачу о ранце:
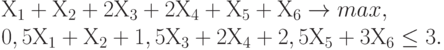
Управляющие параметры 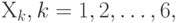 принимают значения из множества, содержащего два элемента - 0 и 1.
принимают значения из множества, содержащего два элемента - 0 и 1.
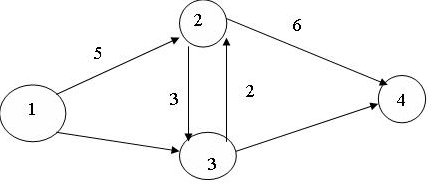
5. Транспортная сеть (с указанием расстояний) приведена на рис. 8.9. Найдите кратчайший путь из пункта 1 в пункт 4.
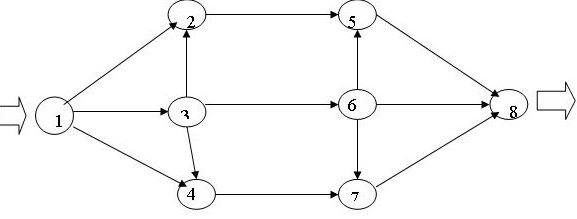
6. Как послать максимальное количество грузов из начального пункта 1 в конечный пункт 8, если пропускная способность путей между пунктами транспортной сети (рис. 8.10) ограничена (табл. 8.7)?
| Пункт отправления | Пункт назначения | Пропускная способность |
|---|---|---|
| 1 | 2 | 1 |
| 1 | 3 | 2 |
| 1 | 4 | 3 |
| 2 | 5 | 2 |
| 3 | 2 | 2 |
| 3 | 4 | 2 |
| 3 | 6 | 1 |
| 4 | 7 | 4 |
| 5 | 8 | 3 |
| 6 | 5 | 2 |
| 6 | 7 | 1 |
| 6 | 8 | 1 |
| 7 | 8 | 3 |
7. Решите задачу коммивояжера для четырех городов (маршрут должен быть замкнутым и не содержать повторных посещений). Затраты на проезд приведены в ттабл. 8.8.
| Город отправления | Город назначения | Затраты на проезд |
|---|---|---|
| А | Б | 2 |
| А | В | 1 |
| А | Д | 5 |
| Б | А | 3 |
| Б | В | 2 |
| Б | Д | 1 |
| В | А | 4 |
| В | Б | 1 |
| В | Д | 2 |
| Д | Ф | 5 |
| Д | Б | 3 |
| Д | В | 3 |
Темы докладов и рефератов
- Классификация оптимизационных задач принятия решений.
- Решения, оптимальные по Парето.
- Многокритериальные задачи принятия решений: различные методы свертки критериев.
- Задачи оптимизации и нечеткие переменные.
- Оптимизация в эконометрических методах принятия решений (на основе монографии [8.5]).
- Место метода множителей Лагранжа в теории оптимизации.