|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Методы повышения экономической эффективности ПКС на основе моделирования и оптимизации внутрикорпоративных потоков
5.4. Компьютерные технологии реализации методов численного моделирования и оптимизации
Настоящий раздел посвящен вопросам разработки компьютерных технологий для нахождения оптимальных величин производственнофинансовых потоков предприятий на простейшем примере некоторой задачи планирования деятельности предприятия. Цель примера - иллюстрация решения задачи планирования систем производственнофинансовых потоков предприятий с применением разрабатываемых ниже методов имитационного моделирования и оптимизации. Основу решения таких задач может составлять применение электронных таблиц. В настоящее время существует ряд известных программных продуктов типа электронных таблиц, таких, как Microsoft Excel и Lotus 1-2-3. Причина выбора электронной таблицы (в качестве основы для создания компьютерных технологий моделирования и оптимизации) состоит в том, что они являются общепринятым стандартом экономикофинансовых расчетов. Среди электронных таблиц из доступных на рынке Microsoft Excel самая простая в эксплуатации и в то же время самая мощная система электронных таблиц. Этот парадокс объясняется простотой использования элементов пользовательского интерфейса, которые обеспечивают доступ к средствам манипулирования данными. Excel всегда имел больше средств для анализа данных, чем другие системы электронных таблиц. Для решения задач оптимизации в Excel имеется надстройка Поиск решения, которая позволяет решать задачи линейного и нелинейного программирования. Excel также имеет встроенные средства для построения разнообразных диаграмм, являющиеся удобным средством представления данных.
Таким образом, Microsoft Excel является наиболее подходящим средством для решения задач планирования и прогнозирования систем внутрипроизводственных потоков предприятий.
Метод имитации с фиксированным шагом моделирования.Во втором разделе настоящей лекции рассматривалась модель системы внутрипроизводственных потоков предприятия. В результате получена система дифференциальных уравнений, описывающая эту модель. Очевидно, полученные зависимости описывают нетривиальные процессы. Поэтому в большинстве случаев применение аналитических методов решения подобных систем дифференциальных уравнений невозможно. Такие системы уравнений следует решать на основе применения численных методов с применением компьютерных программ.
Система уравнений, описывающая некоторую модель внутрипроизводственных потоков, записывается вместе с определенными условиями, устанавливающими способ ее решения. Это система уравнений, которые регулируют изменяющиеся во времени взаимодействия совокупности переменных. Эта изменчивость предопределяет необходимость периодически решать уравнения для нахождения новых состояний системы. В основном система уравнений состоит из уравнений двух типов, соответствующих потокам и накопителям.
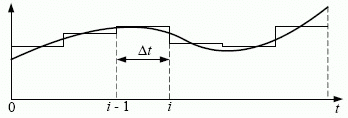
Для каждого момента времени может существовать специфическая последовательность вычислений, определяемая характером системы уравнений. В данном случае сначала рассчитываются величины накопителей, а затем интенсивности потоков. Для этого время квантуется на интервалы времени  , что позволяет аппроксимировать переменные величины с некоторой погрешностью (
рис. 5.31). Интервалы времени должны быть достаточно короткими, чтобы можно было принять допущение о постоянстве величин накопителей и интенсивностей потоков на протяжении интервала, получив при этом удовлетворительное приближение к непрерывно изменяющимся величинам реальной системы. Это означает, что на решения, принятые в начальной точке интервала, не будут влиять изменения, происходящие в течение того же интервала. Новые значения величин накопителей рассчитываются на конец интервала, и по ним определяются новые интенсивности потоков для следующего интервала. Таким образом, выполняется переход от системы дифференциальных уравнений к системе конечноразностных уравнений.
, что позволяет аппроксимировать переменные величины с некоторой погрешностью (
рис. 5.31). Интервалы времени должны быть достаточно короткими, чтобы можно было принять допущение о постоянстве величин накопителей и интенсивностей потоков на протяжении интервала, получив при этом удовлетворительное приближение к непрерывно изменяющимся величинам реальной системы. Это означает, что на решения, принятые в начальной точке интервала, не будут влиять изменения, происходящие в течение того же интервала. Новые значения величин накопителей рассчитываются на конец интервала, и по ним определяются новые интенсивности потоков для следующего интервала. Таким образом, выполняется переход от системы дифференциальных уравнений к системе конечноразностных уравнений.
В принципе можно выбрать столь небольшие интервалы времени, что отрезки прямых, проведенных в пределах каждого интервала, будут сколь угодно близко приближаться к любой кривой ( рис. 5.31). Чем короче и многочисленней будут интервалы, тем более полным будет приближение к кривой. Практически возможно выбирать интервал столь короткий, сколь это необходимо. Однако он должен быть таким, чтобы объем вычислений не превышал возможности применяемых программных средств.
Рассмотрим два последовательных момента времени 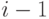 и
и  . Момент
. Момент 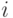 используется для обозначения текущего момента времени, а
используется для обозначения текущего момента времени, а 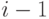 - момент, непосредственно ему предшествующий. Интервал
- момент, непосредственно ему предшествующий. Интервал ![[i-1, i]](/sites/default/files/tex_cache/aedb619943b0af0d419baaa41e1c6f3f.png) только что истек, и информация о нем, как и о предыдущих периодах, может быть использована при решении уравнений. Информация о накопителях и интенсивностях потоков в последующее время вообще недоступна при решении уравнений в настоящий момент времени
только что истек, и информация о нем, как и о предыдущих периодах, может быть использована при решении уравнений. Информация о накопителях и интенсивностях потоков в последующее время вообще недоступна при решении уравнений в настоящий момент времени  .
.
Для целей численного решения основные уравнения модели разделены на две группы: группу уравнений накопителей или запасов и группу уравнений потоков. При рассмотрении какоголибо интервала времени в первую очередь решаются уравнения запасов, а затем полученные результаты используются в уравнениях потоков. Уравнения должны решаться для моментов времени, разделенных 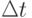 . Уравнения относятся каждый раз к условным моментам времени
. Уравнения относятся каждый раз к условным моментам времени 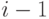 и
и  , причем произвольно принимается, что
, причем произвольно принимается, что 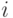 представляет собой текущий момент времени. Другими словами, принимается допущение, что в процессе решения как раз был достигнут момент времени
представляет собой текущий момент времени. Другими словами, принимается допущение, что в процессе решения как раз был достигнут момент времени  , но пока еще не были решены ни уравнения накопителей, ни уравнения потоков в момент времени
, но пока еще не были решены ни уравнения накопителей, ни уравнения потоков в момент времени  .
.
Уравнения запасов показывают, каким образом можно определить накопители в момент  , основываясь на знании накопителей и интенсивностей потоков в момент времени
, основываясь на знании накопителей и интенсивностей потоков в момент времени 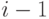 . В момент времени
. В момент времени  , когда решаются уравнения запасов, вся необходимая информация может быть получена и получается из предшествующего интервала времени. Уравнения потоков решаются в настоящий момент
, когда решаются уравнения запасов, вся необходимая информация может быть получена и получается из предшествующего интервала времени. Уравнения потоков решаются в настоящий момент  после того, как решены уравнения запасов. Поэтому значения накопителей в текущий момент
после того, как решены уравнения запасов. Поэтому значения накопителей в текущий момент  могут служить исходными данными для уравнений потоков.
могут служить исходными данными для уравнений потоков.
После определения запасов и интенсивностей потоков в момент  время "индексируется". Это означает, что положение точек
время "индексируется". Это означает, что положение точек 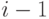 и
и  сдвигается на один интервал времени вправо. Запасы и потоки, только что вычисленные для момента времени
сдвигается на один интервал времени вправо. Запасы и потоки, только что вычисленные для момента времени  , считаются теперь запасами в момент
, считаются теперь запасами в момент 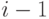 . Текущий момент времени
. Текущий момент времени  сдвигается таким образом на один интервал времени продолжительностью
сдвигается таким образом на один интервал времени продолжительностью 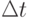 . Всю последовательность вычислений можно теперь повторить для определения нового состояния системы в момент времени более поздний, чем
для предшествующего состояния, на величину
. Всю последовательность вычислений можно теперь повторить для определения нового состояния системы в момент времени более поздний, чем
для предшествующего состояния, на величину 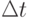 . Интервал
. Интервал  должен быть достаточно коротким, чтобы его величина не влияла скольконибудь серьезно на результаты вычислений. Его следует выбирать по возможности максимально большим для того, чтобы не допускать увеличения загрузки компьютера там, где это не вызвано необходимостью.
должен быть достаточно коротким, чтобы его величина не влияла скольконибудь серьезно на результаты вычислений. Его следует выбирать по возможности максимально большим для того, чтобы не допускать увеличения загрузки компьютера там, где это не вызвано необходимостью.
Основное требование ограничения продолжительности интервала вытекает из характера построения системы уравнений. Запасы определяют потоки, а потоки определяют запасы. В большинстве рассматриваемых систем уравнений допустимый интервал между вычислениями будет определяться такими величинами, как оборачиваемость запаса, период отсрочки оплаты и т. п. То есть теми величинами, которые характеризуют сдвиг одной переменной величины относительно другой по оси времени. Интервал обязательно должен быть меньше любой из подобных величин, желательно, чтобы он был меньше половины наименьшей из них.
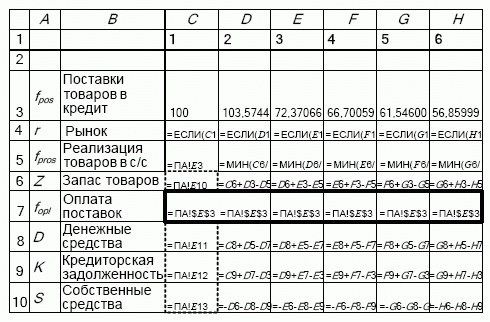
На последующем этапе создается программа в виде электронной таблицы, в которой содержатся уравнения переменных величин. Каждой переменной величине, то есть запасам и потокам, соответствует строка электронной таблицы. Каждый столбец таблицы представляет собой совокупность переменных величин за определенный момент времени. Таким образом, отдельная ячейка таблицы соответствует некоторой переменной величине в определенный момент времени ( рис. 5.32).
Поскольку уравнения для каждой отдельной переменной величины в любой момент времени (за исключением некоторых случаев) одинаковы, формулы для этой переменной величины следует ввести один раз, а для остальных моментов времени уравнения можно получить при помощи применения встроенного в электронную таблицу аппарата копирования формул с использованием относительной адресации. В связи с тем, что для начального момента времени не существует предшествующего, уравнения переменных величин для этого момента времени отличаются от уравнений тех же переменных величин для остальных моментов времени. Такие уравнения носят название уравнений начальных условий.
Как правило, в рассматриваемых моделях одна из переменных величин принимается в качестве управляющей переменной величины, то есть она может задаваться в виде совокупности ее значений на рассматриваемом периоде (на рис. 5.32 переменная величина "Поставки товаров в кредит"). В этом случае остальные переменные величины автоматически пересчитываются при изменении управляющей переменной величины. В результате может быть получен ряд численных решений системы уравнений.
Метод оптимизации с применением компьютерных средств.В предыдущем подразделе рассмотрен метод имитационного моделирования системы внутрипроизводственных потоков предприятия. Как правило, в реальных условиях требуется найти оптимальные величины этих потоков за некоторый промежуток времени, называемый периодом планирования, по некоторому критерию. То есть необходимо найти оптимальные процессы управляющих переменных (переменных управления). Остальные переменные величины будут считаться переменными состояния.
Обозначим:
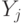 - переменная состояния,
- переменная состояния, 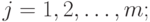
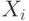 - переменная управления,
- переменная управления, 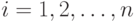 ;
;
 - целевая функция, выраженная через
- целевая функция, выраженная через 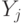 и
и 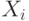 ;
;
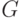 - целевая функция, выраженная только через
- целевая функция, выраженная только через 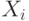 ;
;
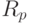 - функция ограничения, выраженная через
- функция ограничения, выраженная через 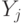 и
и 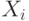 ,
, 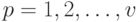 ;
;
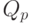 - функция ограничения, выраженная только через
- функция ограничения, выраженная только через 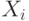 .
.
Наиболее удобной формой модели рассматриваемой системы потоков была бы модель, в которой каждая переменная состояния выражалась бы как функция переменных управления. В такой форме модель системы потоков имеет вид
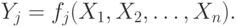 |
( 5.82) |
В том случае, когда целевая функция зависит от переменных состояния и управления, будем говорить, что она представлена в  -форме:
-форме:
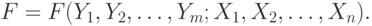 |
( 5.83) |
Подставляя (5.82) в (5.83), можно исключить переменные состояния; в результате получим целевую функцию, которую назовем  -формой:
-формой:
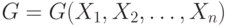 |
( 5.84) |
Аналогичным образом в функции ограничения 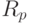 переменные состояния могут быть исключены путем подстановки уравнения (5.82) в
переменные состояния могут быть исключены путем подстановки уравнения (5.82) в 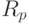 , так что
, так что
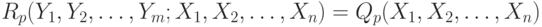
В этом случае задача сводится к оптимизации целевой функции
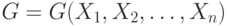
при ограничениях
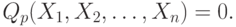
Поскольку в системе уравнений подобной (5.16)-(5.25) содержится ряд зависимостей нелинейного характера, то на практике часто бывает затруднительно выразить целевую функцию и функцию ограничений только через переменные управления. Поэтому в данном случае целесообразно не преобразовывать целевую функцию и функцию ограничений. Так как в процедуре поиска оптимального решения задачи будут применяться компьютерные средства, то такая форма записи выражения для целевой функции и функции ограничений будет вполне приемлемой.
Целевая функция - математическое выражение результата действия процесса. Ее также называют критериальной функцией или показателем качества.
Процесс оптимизации должен сводиться к решению уравнений, которые можно использовать для нахождения переменных управления, оптимизирующих целевую функцию. Уравнения, которые выражают переменные оптимального управления через требуемые параметры работы, называются уравнениями оптимального управления.
Ограничения на переменные состояния и переменные управления либо ограничивают область допустимых значений переменных состояния и переменных управления, либо устанавливают дополнительные зависимости между переменными состояния и переменными управления. При оптимизации реальных процессов ограничения имеются всегда. В некотором смысле ограничения на переменные состояния и переменные управления можно считать расширением модели процесса. Это связано с тем, что ограничения определяют зависимость между переменными состояния и переменными управления, а также допустимую область протекания процесса.
Ограничения играют большую роль при оптимизации. Например, линейная целевая функция, применяемая при линейном программировании, вообще не имеет экстремума, если отсутствуют ограничения. С другой стороны, ограничения на переменные управления обычно отрицательно сказываются на качестве оптимального процесса.
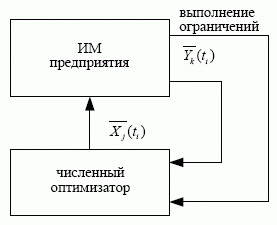
В рассматриваемой модели в качестве управляющих переменных могут использоваться такие величины, как поставки товаров в кредит, получение/возврат банковских ссуд, график запуска производства и т. п. В соответствии с предложенным выше методом имитационного моделирования управляемая переменная представляет собой последовательность ее значений в разные моменты времени. Поскольку оптимизации подлежит процесс (управляемая величина), эти значения оптимизируются как совокупность независимых скалярных величин. На рис. 5.33 представлена схема проведения оптимизации с применением поискового оптимизатора, встроенного в электронную таблицу.
Укрупненно процедуру проведения поиска оптимального решения можно представить следующим образом. На начальном этапе задаются некоторые начальные значения варьируемых (управляющих) переменных. Затем проверяется выполнение заданных ограничений.
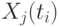 - значение j-й переменной управления в момент времени
- значение j-й переменной управления в момент времени 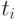 ,
, 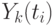 - значение k-й переменной состояния в момент времени
- значение k-й переменной состояния в момент времени 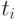
Если все ограничения выполняются, то производится расчет значения целевой функции. Затем управляющие переменные изменяются некоторым образом с целью получения "лучшего" значения критериальной функции, после чего производится новая проверка выполнения ограничений.
Если какоелибо ограничение не выполняется, то значения управляющих переменных изменяются с тем, чтобы все ограничения выполнялись.
Далее описанные действия повторяются до тех пор, пока не будет получено либо наилучшее решение, либо заключение о несходимости модели, либо заключение об отсутствии области допустимых значений управляющих переменных, то есть о невозможности одновременного выполнения всех ограничений. Последние два случая могут быть связаны с неправильной постановкой задачи или с некорректными исходными данными.
Описанная процедура поиска оптимального решения используется во встроенном в Excel поисковом оптимизаторе Поиск решения (Solver). Это средство обладает достаточно развитыми возможностями, такими, как задание множества управляющих переменных, выбор метода поиска решения, что делает его приемлемым для решения задач оптимизации.
Для применения оптимизатора, встроенного в электронную таблицу, необходимо:
- построить имитационную модель внутрипроизводственных потоков предприятия так, как это было показано в предыдущем параграфе;
- ввести формулу расчета целевой функции в соответствующую ячейку электронной таблицы на том же листе, где представлены рассчитываемые величины;
- настроить поисковый оптимизатор, то есть указать ячейки, содержащие варьируемые величины, ячейку с целевой функцией, задать ограничения и, возможно, изменить параметры оптимизатора (погрешность вычислений, оценка, метод вычисления производных и т. п.);
- запустить оптимизатор.
Пример задачи планирования производственнофинансовых потоков предприятия.
Рассмотрим приведенную во второй лекции задачу планирования деятельности гипотетического простейшего предприятия. Ниже эта задача будет решаться на основе применения разработанных методов моделирования и оптимизации. На рис. 5.34 приведена поточнофинансовая структура рассматриваемой модели функционирования простейшего предприятия.
 - запас товаров в ценах приобретения,
- запас товаров в ценах приобретения,  - денежные средства,
- денежные средства, 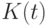 - кредиторская задолженность,
- кредиторская задолженность,  - собственные средства,
- собственные средства,  - поставки,
- поставки,  - продажи, в себестоимости приобретения товаров,
- продажи, в себестоимости приобретения товаров,  - оплата поставок,
- оплата поставок, 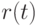 - рыночная среда
- рыночная среда
Такая модель, как было показано в первом разделе настоящей лекции, описывается системой уравнений (5.16)-(5.25). Эта система уравнений моделирует непрерывные величины, поэтому для решения рассматриваемой задачи методом имитации и оптимизации ее постановка требует уточнения.
Запишем уравнения, описывающие приведенную структуру в соответствии с рассмотренным выше методом имитационного моделирования. Разобьем период планирования деятельности предприятия ![[t_{0}, t_{pl}]](/sites/default/files/tex_cache/ddc2903b057afe5fc531285f698f81b8.png) на отрезки "единичной" длины
на отрезки "единичной" длины 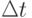 . Поскольку предполагается, что период планирования составляет порядка одного года, то за отрезок "единичной" длины примем, например, одну неделю. В результате проведенного разбиения мы получим
. Поскольку предполагается, что период планирования составляет порядка одного года, то за отрезок "единичной" длины примем, например, одну неделю. В результате проведенного разбиения мы получим  таких отрезков. Обозначим индекс единичных отрезков через
таких отрезков. Обозначим индекс единичных отрезков через  . Таким образом,
. Таким образом, 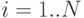 . Рассмотрим переменные величины запасов и потоков в некоторые моменты
. Рассмотрим переменные величины запасов и потоков в некоторые моменты 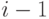 и
и  внутри интервала планирования. Будем считать, что текущим моментом времени является момент времени
внутри интервала планирования. Будем считать, что текущим моментом времени является момент времени  .
.
Поставки оплачиваются с отсрочкой на период 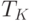 . Поэтому функция оплаты
. Поэтому функция оплаты  - это функция поставок, сдвинутая вправо по оси времени на период
- это функция поставок, сдвинутая вправо по оси времени на период 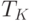 . Для упрощения расчетов будем считать, что единицы измерения
. Для упрощения расчетов будем считать, что единицы измерения 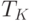 ,
, 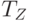 и единичных отрезков совпадают. Тогда
и единичных отрезков совпадают. Тогда
 |
( 5.85) |
Выручка от продаж накапливается в виде денежных средств и расходуется на оплату поставок, а также вся прибыль изымается из оборота в виде дивидендов. Поэтому на ПФС предприятия не изображены потоки прибыли и дивидендов.
Интенсивность потока продаж в модели зависит от рыночного спроса 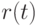 и величины запаса товаров
и величины запаса товаров  . Считается, что продажи не могут превышать рыночные ограничения, а также максимальную величину, которую позволяет текущий запас товаров:
. Считается, что продажи не могут превышать рыночные ограничения, а также максимальную величину, которую позволяет текущий запас товаров:
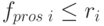 |
( 5.86) |
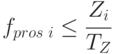 |
( 5.87) |
где 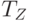 - показатель оборачиваемости запаса товаров, измеряемый в единицах времени.
- показатель оборачиваемости запаса товаров, измеряемый в единицах времени.
В соответствии с формализованной постановкой задачи, выполненной во второй лекции, в качестве переменных управления выбраны две величины: поставки и реализация. Поскольку целью рассматриваемого решения задачи является иллюстрация применения методов имитационного моделирования и оптимизации, то для более ясного понимания использования этих методов за переменную управления примем только интенсивность поставок. Тогда для исключения неоднозначности в определении интенсивности реализации примем допущение о том, что эта величина является минимальной из двух величин: 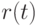 и
и 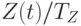 . Другими словами,
. Другими словами,
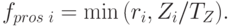 |
( 5.88) |
Согласно методологии ПФС количественные связи между содержимым блоков и интенсивностями потоков задаются в следующем виде: скорость изменения содержимого блока равна разности интенсивностей входящих и исходящих потоков:
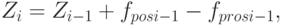 |
( 5.89) |
 |
( 5.90) |
 |
( 5.91) |
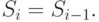 |
( 5.92) |
Как следствие (5.92), можно записать следующее:
 |
( 5.93) |
В связи с тем, что, согласно методологии ПФС, активы представляют собой неотрицательные величины, а источники средств - неположительные, имеем
 |
( 5.94) |
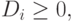 |
( 5.95) |
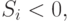 |
( 5.96) |
 |
( 5.97) |
Поскольку по условию задачи поставляемые поставщиками и реализуемые покупателям товары не могут быть возвращены обратно, то
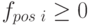 |
( 5.98) |
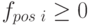 |
( 5.99) |
Функция потока оплаты поставок представляет собой сдвинутую вправо по оси времени на период 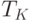 функцию поставок. В силу неотрицательности последней
функцию поставок. В силу неотрицательности последней
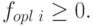 |
( 5.100) |
Поскольку в начальный момент существования предприятие располагало только собственными средствами, равными денежным, то
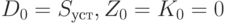 |
( 5.101) |
С учетом (5.89)-(5.91) и (5.101) получаем баланс активов и источников средств:
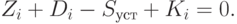 |
( 5.102) |
Функционирование предприятия описывается системой уравнений (5.85), (5.88) - (5.102) и рассматривается на плановом периоде ![[t_{0}, t_{pl} ]](/sites/default/files/tex_cache/b1b1b4157a2cab25a94e468c3eee4f7e.png) , где
, где 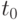 и
и 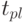 - моменты времени начала и окончания периода соответственно (или
- моменты времени начала и окончания периода соответственно (или 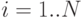 , где
, где 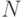 - число отрезков единичной длины, на которые разбит интервал планирования), а также тремя величинами - параметрами предприятия -
- число отрезков единичной длины, на которые разбит интервал планирования), а также тремя величинами - параметрами предприятия -  ,
, 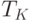 и
и 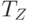 .
.
Существенным обстоятельством является факт влияния процесса функционирования до некоторого момента на процесс функционирования после этого момента. Такое влияние возникает, поскольку в данный текущий момент оплачиваются предшествующие поставки. Поэтому процесс функционирования предприятия после начала планового периода зависит от процесса функционирования на отрезке до начала планового периода. Следовательно, возникает необходимость задать состояние предприятия до момента 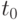 не как значения интенсивностей потоков и содержимого накопителей, а как специальным образом определяемый и задаваемый исходный процесс функционирования. Таким процессом естественно считать функционирование в условиях постоянства потоков и содержимого накопителей - стабильное, невозмущенное функционирование. По этим же причинам в задаче планирования следует потребовать перевода производственной системы в новое стабильное состояние. Если невозмущенность функционирования после момента
не как значения интенсивностей потоков и содержимого накопителей, а как специальным образом определяемый и задаваемый исходный процесс функционирования. Таким процессом естественно считать функционирование в условиях постоянства потоков и содержимого накопителей - стабильное, невозмущенное функционирование. По этим же причинам в задаче планирования следует потребовать перевода производственной системы в новое стабильное состояние. Если невозмущенность функционирования после момента 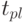 не потребовать, то увеличение рентабельности при постоянстве собственных средств возможно при увеличении поставок на отрезке
не потребовать, то увеличение рентабельности при постоянстве собственных средств возможно при увеличении поставок на отрезке ![[t_{pl} -T_{K}, t_{pl} ]](/sites/default/files/tex_cache/10e964e0e88393e95e35657e7565a08c.png) , так как оплата этих поставок потребуется уже после окончания планового периода, что не повлияет на рентабельность (поскольку критерий рентабельности рассчитывается лишь для данного планового периода).
, так как оплата этих поставок потребуется уже после окончания планового периода, что не повлияет на рентабельность (поскольку критерий рентабельности рассчитывается лишь для данного планового периода).
Обратимся теперь к анализу параметров стабильного функционирования. Связь величины содержимого накопителя 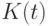 с интенсивностями входных и выходных потоков в условиях стабильности можно выяснить на основе представления о времени полного обновления этого содержимого. По определению стабильного функционирования все потоки равны и, в частности, входной поток блока
с интенсивностями входных и выходных потоков в условиях стабильности можно выяснить на основе представления о времени полного обновления этого содержимого. По определению стабильного функционирования все потоки равны и, в частности, входной поток блока 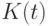 равен выходному. Обозначим интенсивность этих потоков в стабильном функционировании новой переменной величиной
равен выходному. Обозначим интенсивность этих потоков в стабильном функционировании новой переменной величиной 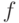 . Тогда содержимое блока
. Тогда содержимое блока 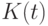 полностью обновляется за время
полностью обновляется за время 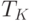 , так как это время отсрочки оплаты поставок:
, так как это время отсрочки оплаты поставок:
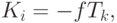 |
( 5.103) |
(знак "минус", поскольку источники средств представляются неположительными величинами).
Для начального состояния системы потоков соотношение (5.103) будет выполняться автоматически в силу задания начальных условий (как будет показано ниже). Для конечного состояния уравнение (5.103) следует задать как ограничение, налагаемое на систему потоков. Кроме того, по условию стабильного функционирования следует задать постоянство интенсивности потока поставок на отрезке
![f_{pos\text{ } i} |_{i \in [N -T_к, N]} = f_{pos\text{ } N} = const.](/sites/default/files/tex_cache/e7ab87b9abee6368b513df7e7fa2421c.png) |
( 5.104) |
Из этого ограничения следует, что к моменту времени 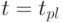 или при
или при 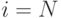 интенсивность потока оплаты
интенсивность потока оплаты 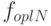 будет равна
будет равна  в силу уравнения (5.85). Поэтому ограничение на равенство потока поставок и их оплаты в момент
в силу уравнения (5.85). Поэтому ограничение на равенство потока поставок и их оплаты в момент 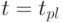 задавать не нужно.
задавать не нужно.
Чтобы система потоков находилась в стабильном состоянии, следует задать ограничение (5.103), где в качестве  принимается величина
принимается величина  , а также равенство
, а также равенство  и
и  в момент
в момент 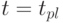
 |
( 5.105) |
Таким образом, уточненная постановка задачи выглядит следующим образом: для производственной системы ( рис. 5.34) найти план поставок на плановом периоде, обеспечивающий максимум продаж, при условиях:
- до начала планового периода производственная система находилась в известном состоянии стабильного функционирования;
- после окончания планового периода производственная система находится в некотором состоянии стабильного функционирования;
- спрос на товары скачкообразно изменяется в момент времени внутри планового периода.
Так как производственная система с "памятью" в силу (5.85), то состояние предприятия в начале периода планирования можно задать значениями пяти переменных величин:
 , и совокупностью значений функции оплаты поставок на отрезке
, и совокупностью значений функции оплаты поставок на отрезке ![[t_{0}, t_{0} + T_{K}]: f_{opl}_{i}|_
{i \in [1, T_{K} ]}](/sites/default/files/tex_cache/6d1be0f4b1efde9d23765d5e6220877d.png)
В формализованном виде задачу можно представить следующим образом:
Дано:
- параметры предприятия
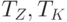 и
и  ;
; - начальное состояние предприятия:
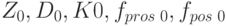 и
и ![f_{opl\text{ }i}|_{I \in [1, T_{K} ]}](/sites/default/files/tex_cache/08a9bf747e6981513f7d7fa731671db5.png) ;
; - рынок на периоде планирования
![r_{i}|_{ i \in[1,N]}](/sites/default/files/tex_cache/374f8c73b9744cd723ef00f41dbf6c05.png)
Найти:
![f_{pos\text{ } i}|_{ i \in [1, N ]}](/sites/default/files/tex_cache/f427ac37d8f797d04003aaa92405efdc.png) , удовлетворяющие уравнениям (5.85), (5.88)-(5.102) и обеспечивающие максимум продаж:
, удовлетворяющие уравнениям (5.85), (5.88)-(5.102) и обеспечивающие максимум продаж: 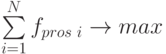 при выполнении ограничений (5.94)-(5.100), (5.103)- (5.105).
при выполнении ограничений (5.94)-(5.100), (5.103)- (5.105).
Таким образом, уточнена формализованная постановка задачи для применения метода имитации и оптимизации, что позволяет применить Excel для ее численного решения.