Функциональные зависимости и реляционные базы данных

Аксиомы вывода функциональных зависимостей

Известно, что функции могут образовывать пространства, и в пространствах выполняются различные операции. В нашем случае для каждой базы данных на множестве ее отношений можно рассмотреть все возможные, допустимые в семантическом смысле функциональные зависимости. Для каждого отношения существует вполне определенное множество ФЗ между его атрибутами. На практике число рассматриваемых атрибутов и ФЗ конечно (!).

Поскольку ФЗ являются высказываниями об атрибутах сущностей предметной области, то над ними могут быть определены операции, позволяющие логически получать одну зависимость из другой (или устанавливать между ними эквивалентность). Это позволяет определить для данной схемы базы данных базовый набор ФЗ, из которого может быть выведено все множество ФЗ, присущих этой схеме. Данное утверждение является третьей (3) конструктивной идеей в теории проектирования реляционных баз данных.

Математически эту задачу можно поставить следующим образом. Пусть U {A₁, A₂, ..., A_n} - универсальное множество атрибутов, т.е. полный набор атрибутов отношения базы данных. Совокупность пар (X, Y), таких, что 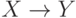, задает структуру ФЗ отношения R. Такое отношение называют еще универсальным отношением. Задача состоит в построении такого набора ФЗ, из которого могут быть получены все ФЗ базы данных.

Например, транзитивную ФЗ в отношении r можно логически вывести из и . Пусть отношение содержит два кортежа - t и s, совпадающие по атрибуту А, но не совпадающие по С. Нужно выяснить, совпадают ли кортежи t и s по атрибуту В. Если это не так, то нарушается зависимость . Если существует совпадение для В, то, поскольку по условию не совпадают компоненты по С, то будет нарушена зависимость . Таким образом, отношение удовлетворяет зависимости .

Такие рассуждения позволяют ввести следующие определения.

Определение 7. Пусть F - множество ФЗ для схемы отношения r, - некоторая ФЗ. Говорят, что ФЗ логически следует из F, если для каждого отношения R со схемой r, удовлетворяющего ФЗ из F, удовлетворяется также зависимость .

В примере выше мы видели, что если F содержит ФЗ из и , то зависимость логически следует из F.

Определение 8. Пусть F - множество ФЗ для схемы отношения r. Тогда замыканием F⁺ множества ФЗ F называется множество ФЗ, которое логически следует из F. F называется полным семейством ФЗ, если F⁺ = F.

Пример (без доказательства). Пусть 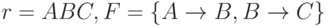. Тогда F⁺ состоит из всех зависимостей 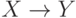, таких, что выполняется одно из следующих условий:

• X содержит A, т.е. 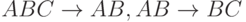или ;
• X содержит B, но не A, и Y не содержит A, т.е. 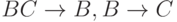или B ;
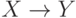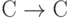• есть или .

Теперь можно уточнить понятие ключа отношения. Предполагается, что для сущностей предметной области существует множество атрибутов, которое уникально определяет каждую из этих сущностей. Понятие замыкания позволяет дать формальное определение ключу отношения.

Определение 9. Пусть F - множество ФЗ для схемы отношения R(A₁, A₂, ..., A_n). Подмножество атрибутов X называется ключом отношения R, если ФЗ: принадлежит F⁺ и не для какого собственного подмножества ФЗ: не принадлежит F⁺.

Таким образом, заданный аналитиком ключ некоторого набора сущностей предметной области только тогда является ключом отношения, представляющего эти сущности в реляционной базе данных, когда он является минимальным ключом, т.е. содержит минимальное подмножество ключевых атрибутов. При определении ключа сущности предметной обычно невозможно установить свойство минимальности ввиду отсутствия формальной разработки для этой процедуры. На практике существует несколько наборов атрибутов сущности предметной области в качестве кандидатов на ключ отношения. Проектировщик базы данных может выбрать любой из них для идентификации отношения. Для того чтобы выделять ситуацию множественности в выборе ключа, для обозначения ключа сущности пользуйтесь термином возможный ключ.

Пример. Многозначность при выборе ключа