|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Организационно-экономическая система управления материальными запасами промышленных корпоративных систем
4.3. Управление материальными запасами для нестационарных детерминированных условий
Метод динамического программирования.Чтобы использовать метод динамического программирования в решении приведенной выше оптимизационной задачи, приведем общую постановку задачи динамического программирования [5].
Рассматривается управляемый процесс, в данном случае процесс нахождения оптимальной стратегии управления запасами. В результате управления система (объект управления)  переводится из начального состояния
переводится из начального состояния  в состояние
в состояние 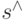 . Предположим, что управление можно разбить на
. Предположим, что управление можно разбить на  шагов, т. е. решение принимается последовательно на каждом шаге, а управление, переводящее систему
шагов, т. е. решение принимается последовательно на каждом шаге, а управление, переводящее систему  из начального состояния в конечное, представляет собой совокупность
из начального состояния в конечное, представляет собой совокупность  пошаговых управлений. Обозначим через
пошаговых управлений. Обозначим через 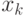 управление на
управление на  -м шаге (
-м шаге ( 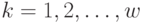 ). Если управления
). Если управления 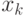 удовлетворяют некоторым ограничениям решаемой задачи, то такие управления являются допустимыми (
удовлетворяют некоторым ограничениям решаемой задачи, то такие управления являются допустимыми ( 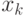 может быть числом, точкой в
может быть числом, точкой в  -мерном пространстве, функцией, значением качественного признака, иным объектом нечисловой природы).
-мерном пространстве, функцией, значением качественного признака, иным объектом нечисловой природы).
Пусть 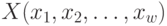 - управление, переводящее систему
- управление, переводящее систему  из состояния
из состояния  в состояние
в состояние 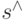 . Обозначим через
. Обозначим через 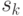 состояние системы после
состояние системы после  -го шага управления (
-го шага управления ( 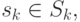 где
где 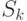 - множество всех возможных состояний на шаге
- множество всех возможных состояний на шаге  ). Получаем последовательность состояний
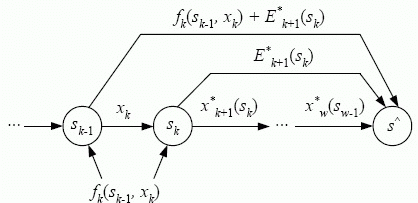
). Получаем последовательность состояний  Пошаговый процесс перехода системы
Пошаговый процесс перехода системы  из состояния
из состояния  в состояние
в состояние 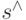 под действием управления
под действием управления 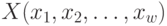 представлен на рис. 4.12.
представлен на рис. 4.12.
Для данного процесса действуют следующие положения:
- Состояние
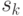 системы в конце
системы в конце  -го шага зависит от предшествующего состояния
-го шага зависит от предшествующего состояния 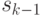 и управления на
и управления на  -м шаге
-м шаге 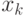 (и не зависит от предшествующих состояний и управлений). Это требование называется "отсутствием последствия". Сформулированное положение записывается в виде уравнений:
(и не зависит от предшествующих состояний и управлений). Это требование называется "отсутствием последствия". Сформулированное положение записывается в виде уравнений: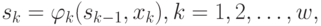
( 4.19) которые называются уравнениями состояний.
- Эффективность каждого
 -го шага также зависит от предшествующего состояния
-го шага также зависит от предшествующего состояния 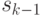 и управления на
и управления на  -м шаге
-м шаге 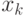 . Обозначим эффективность
. Обозначим эффективность  -го шага через
-го шага через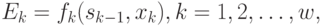
тогда эффективность всего управления
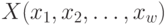 определяется как
определяется как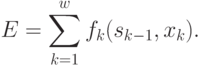
( 4.20)
Задача пошаговой оптимизации (задача динамического программирования) формулируется следующим образом: определить такое допустимое управление  , переводящее систему
, переводящее систему  из состояния
из состояния  в состояние
в состояние  , при котором целевая функция (4.20) принимает наибольшее (наименьшее) значение.
, при котором целевая функция (4.20) принимает наибольшее (наименьшее) значение.
Решение поставленной задачи с помощью метода динамического программирования заключается в последовательной минимизации целевой функции за 1, 2 и т. д. интервала на основе принципа оптимальности Р. Беллмана: каково бы ни было состояние s системы в результате какоголибо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.
Рассмотрим последовательно определение оптимального управления на шаге 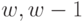 и т. д., используя принцип оптимальности Р. Беллмана.
и т. д., используя принцип оптимальности Р. Беллмана.
Рассмотрим  -й шаг:
-й шаг:
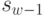 - состояние системы к началу
- состояние системы к началу  -го шага
-го шага 
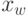 - управление на
- управление на  -м шаге;
-м шаге;
 - целевая функция (выигрыш)
- целевая функция (выигрыш) 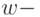 го шага.
го шага.
Согласно принципу оптимальности, 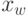 нужно выбирать так, чтобы для любых состояний
нужно выбирать так, чтобы для любых состояний 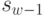 получить максимум целевой функции на этом шаге. Обозначим через
получить максимум целевой функции на этом шаге. Обозначим через 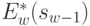 максимум целевой функции - показателя эффективности
максимум целевой функции - показателя эффективности  -го шага при условии, что к началу последнего шага система
-го шага при условии, что к началу последнего шага система  была в произвольном состоянии
была в произвольном состоянии 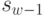 , а на последнем шаге управление было оптимальным.
, а на последнем шаге управление было оптимальным.
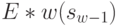 называется условным максимумом целевой функции на w-м шаге:
называется условным максимумом целевой функции на w-м шаге:
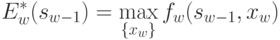 |
( 4.21) |
Максимизация ведется по всем допустимым управлениям 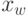 .
.
Решение 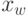 , при котором достигается
, при котором достигается 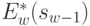 , также зависит от
, также зависит от 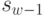 и называется условным оптимальным управлением на w-м шаге и обозначается
и называется условным оптимальным управлением на w-м шаге и обозначается 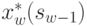 .
.
Решив одномерную задачу локальной оптимизации по уравнению (4.21) для всех возможных состояний 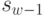 , находятся две функции:
, находятся две функции: 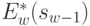 и
и 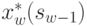 .
.
Рассмотрим теперь двухшаговую задачу: присоединим к  -му шагу (
-му шагу ( 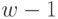 )-й.
)-й.
Для любых состояний 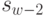 , произвольных управлений
, произвольных управлений 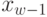 и оптимальном управлении на
и оптимальном управлении на  -м шаге значение целевой функции на двух последних шагах:
-м шаге значение целевой функции на двух последних шагах:
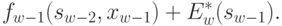 |
( 4.22) |
Согласно принципу оптимальности для любых 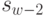 решение нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем (
решение нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем (  -м) шаге приводило бы к максимуму целевой функции на двух последних шагах. Следовательно, необходимо найти максимум выражения (4.22) по всем допустимым управлениям
-м) шаге приводило бы к максимуму целевой функции на двух последних шагах. Следовательно, необходимо найти максимум выражения (4.22) по всем допустимым управлениям 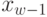 . Максимум этой суммы зависит от
. Максимум этой суммы зависит от 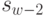 , обозначается через
, обозначается через 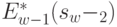 и называется условным максимумом целевой функции при оптимальном управлении на двух последних шагах. Соответствующее управление
и называется условным максимумом целевой функции при оптимальном управлении на двух последних шагах. Соответствующее управление 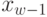 на (
на ( 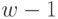 )-м шаге обозначается через
)-м шаге обозначается через 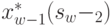 и называется условным оптимальным управлением на (
и называется условным оптимальным управлением на ( 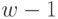 )-м шаге.
)-м шаге.
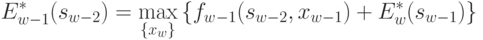 |
( 4.23) |
С учетом уравнения состояния 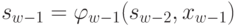 значение целевой функции зависит только от
значение целевой функции зависит только от 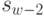 и
и 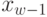 . В результате максимизации только по одной переменной
. В результате максимизации только по одной переменной 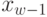 согласно уравнению (4.23) вновь получаем две функции:
согласно уравнению (4.23) вновь получаем две функции: 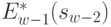 и
и 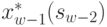 .
.
Далее рассматривается трехшаговая задача: к двум последним шагам присоединяется 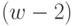 -й и т. д.
-й и т. д.
Рассмотрим общий случай определения оптимального управления на шаге  (
( 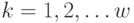 ). Обозначим через
). Обозначим через 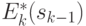 условный максимум целевой функции, полученный при оптимальном управлении на
условный максимум целевой функции, полученный при оптимальном управлении на 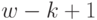 шагах, начиная с
шагах, начиная с  -го до конца, при условии, что к началу
-го до конца, при условии, что к началу  -го шага система находилась в состоянии
-го шага система находилась в состоянии 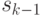 . Фактически эта функция равна:
. Фактически эта функция равна:
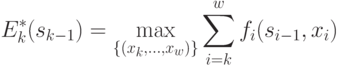
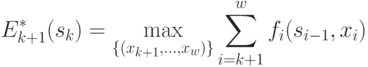
С другой стороны, целевая функция на 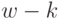 последних шагах (рис. 4.13) при произвольном управлении
последних шагах (рис. 4.13) при произвольном управлении 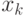 на
на  -м шаге и оптимальном управлении на последующих шагах равна
-м шаге и оптимальном управлении на последующих шагах равна
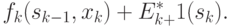 |
( s_{k})) |
Согласно принципу оптимальности, 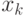 выбирается из условия максимума этой суммы, т. е.
выбирается из условия максимума этой суммы, т. е.
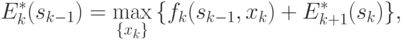 |
( 4.24) |
где 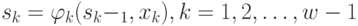 .
.
Таким образом, определив из (4.21) значения 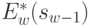 и
и 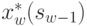 , а из (4.24) и уравнений состояний (4.19) значения
, а из (4.24) и уравнений состояний (4.19) значения 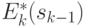 и соответствующие
и соответствующие 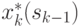 получим последовательности:
получим последовательности:
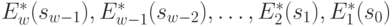 -
-
условные максимумы целевой функции на последнем, на двух последних, на 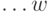 последних шагах и
последних шагах и
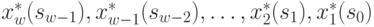 -
-
условные оптимальные управления на  -м,
-м,  -м,
-м,  ,
,  -м шагах.
-м шагах.
Используя эти последовательности, можно найти решение задачи при данных  и
и  . При фиксированном
. При фиксированном  получаем
получаем 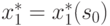 . Далее из (4.19) определяется
. Далее из (4.19) определяется 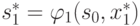 и т. д.:
и т. д.:
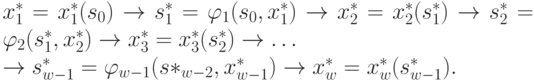
Таким образом, получаем оптимальное решение задачи:
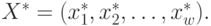
Постановка задачи определения оптимальной стратегии нестационарной детерминированной системы управления запасами для решения методом динамического программирования.Чтобы разработать алгоритм решения поставленной в разделе 4.2 оптимизационной задачи, опишем ее в терминах динамического программирования. Объектом управления в данном случае является рассмотренная выше система управления запасами. Управление системой разбивается на  пошаговых управлений
(
пошаговых управлений
( 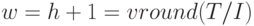 - максимальное количество возможных поставок в течение периода планирования
- максимальное количество возможных поставок в течение периода планирования  , увеличенное на единицу).
, увеличенное на единицу).
Управление 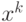 , переводящее систему
, переводящее систему  из состояния
из состояния 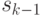 в состояние
в состояние 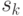 , представляет собой величину и момент времени
, представляет собой величину и момент времени  -й поставки.
-й поставки.
В общем случае величина поставки продукции на склад может принимать множество значений  :
:
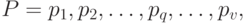
где 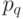 - объем
- объем  -го варианта поставки продукции.
-го варианта поставки продукции.
Возможные варианты размеров поставок продукции могут быть определены исходя из ограничений (4.17):
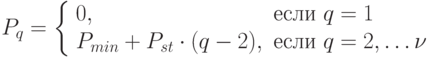 |
( 4.25) |
Общее количество вариантов поставки 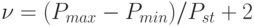 .
.
Каждая поставка 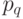 может быть произведена в любой момент времени
может быть произведена в любой момент времени  (в общем случае
(в общем случае 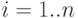 ).
).
Таким образом, множество возможных управлений 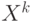 на шаге
на шаге  можно представить в виде следующей матрицы порядка
можно представить в виде следующей матрицы порядка  :
:
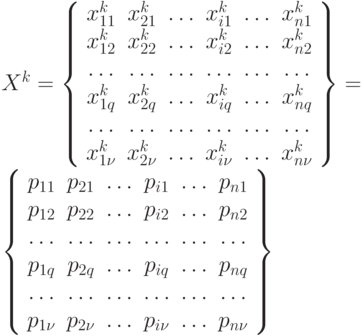
Управление 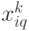 представляет собой поставку объемом
представляет собой поставку объемом 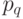 в момент времени
в момент времени  на шаге
на шаге  .
.
Каждое управление 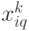 переводит систему в соответствующее состояние
переводит систему в соответствующее состояние 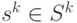 , поэтому размерность множества состояний
, поэтому размерность множества состояний 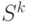 такая же, как и размерность множества возможных управлений
такая же, как и размерность множества возможных управлений 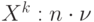 . Множество возможных состояний
. Множество возможных состояний 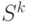 можно представить в виде следующей матрицы:
можно представить в виде следующей матрицы:
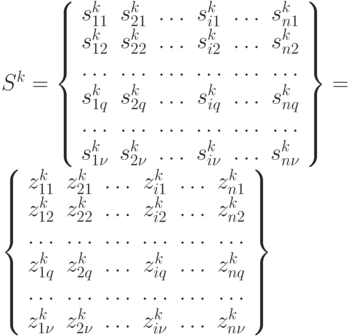
Каждое состояние 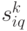 представляет собой величину запаса
представляет собой величину запаса 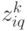 в момент времени
в момент времени  после поставки
после поставки 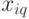 .
.
Получим уравнение состояний для данной задачи. Из балансового уравнения (2.5)  следует:
следует:
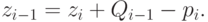 |
( 4.26) |
Из условия задачи в конце планового периода в момент времени  система должна находиться в состоянии
система должна находиться в состоянии 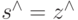 . Тогда из (4.26) следует:
. Тогда из (4.26) следует:
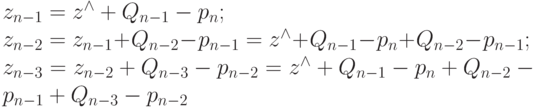
и т. д.
В общем случае получим:
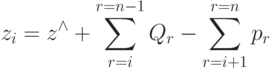 |
( 4.27) |
Предположим, что под воздействием управления 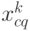 система переходит из состояния
система переходит из состояния 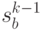 в состояние
в состояние 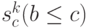 , где
, где 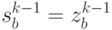 - уровень запаса в системе в момент времени
- уровень запаса в системе в момент времени  после
после  -й поставки;
-й поставки;
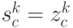 - уровень запаса в системе в момент времени
- уровень запаса в системе в момент времени  после
после  -й поставки.
-й поставки.
Из (4.27) следует:
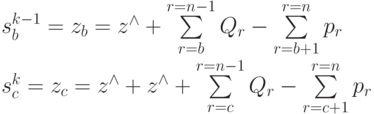
Преобразовав систему этих двух уравнений, получим:
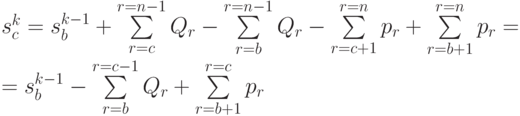 |
( 4.28) |
Последняя сумма в данном выражении - сумма поставок с момента ( 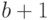 ) до момента
) до момента  и равна
и равна 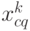 , следовательно:
, следовательно:
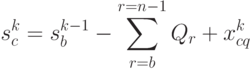
Уравнение (4.28) - это уравнение состояний для решаемой задачи.
Выразим эффективность  -го шага, которая зависит от предшествующего состояния
-го шага, которая зависит от предшествующего состояния 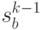 и управления на
и управления на  -м шаге
-м шаге 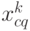 , переводящего систему в состояние
, переводящего систему в состояние 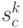 . Эффективность
. Эффективность  -го шага выражается из (4.16) и равна величине совокупных затрат, возникающих на шаге
-го шага выражается из (4.16) и равна величине совокупных затрат, возникающих на шаге  :
:
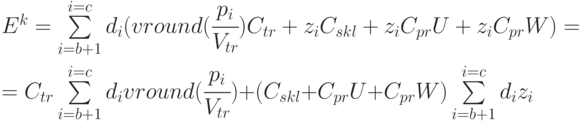 |
( 4.29) |
Первое слагаемое в выражении (4.29) представляет собой стоимость транспортировки товара, поставленного на склад с момента времени ( 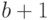 ) до момента времени
) до момента времени  , приведенную к началу отчетного периода с учетом дисконтфактора
, приведенную к началу отчетного периода с учетом дисконтфактора  . Поскольку на шаге
. Поскольку на шаге  при управлении
при управлении 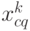 производится всего лишь одна поставка товара в момент времени
производится всего лишь одна поставка товара в момент времени  в размере
в размере 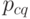 , то:
, то:
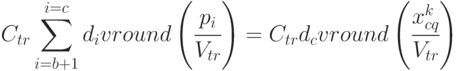 |
( 4.30) |
Преобразуем второе слагаемое выражения (4.29):
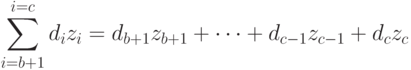
Поскольку за период времени с  по
по  запас не пополняется, а только расходуется, то из (4.18) получим:
запас не пополняется, а только расходуется, то из (4.18) получим:
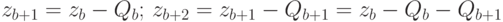 и т. д.
и т. д.
Таким образом, при  величину запаса в момент
величину запаса в момент  можно выразить как:
можно выразить как:
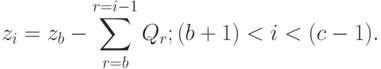
В момент времени  производится поставка продукции в размере
производится поставка продукции в размере 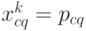 , поэтому из (4.18) имеем:
, поэтому из (4.18) имеем:
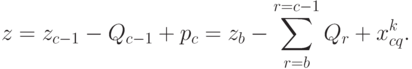
Таким образом, второе слагаемое в выражении (4.29) можно записать как:
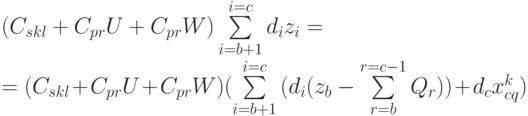 |
( 4.31) |
Подставив (4.30) и (4.31) в (4.29), получим:
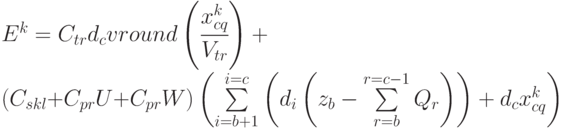 |
( 4.32) |
Величина 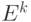 в (4.32) - эффективность
в (4.32) - эффективность  -го шага, а именно величину совокупных затрат на создание и пополнение запаса с момента
-го шага, а именно величину совокупных затрат на создание и пополнение запаса с момента 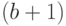 (начало шага
(начало шага 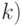 и до момента c (конец шага
и до момента c (конец шага 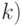 , если в момент
, если в момент  система находилась в состоянии
система находилась в состоянии 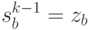 , и затем было выбрано управление
, и затем было выбрано управление 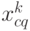 .
.
Просуммировав 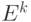 для каждого шага
для каждого шага 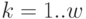 , получим величину совокупных затрат на создание и пополнение запаса в течение планового периода
, получим величину совокупных затрат на создание и пополнение запаса в течение планового периода  :
:
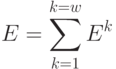 |
( 4.33) |
Таким образом, необходимо решить следующую задачу: определить такое допустимое управление  , переводящее систему
, переводящее систему  из состояния
из состояния  в состояние
в состояние  , при котором целевая функция (4.33) принимает наименьшее значение.
, при котором целевая функция (4.33) принимает наименьшее значение.


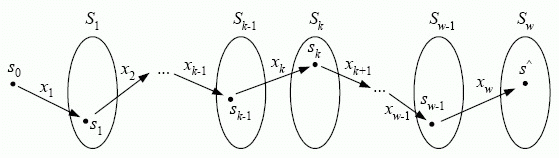
 - конечное
- конечное