Теорема 1.3. Пусть выполняются условия
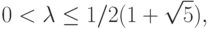 |
(
5.11)
|
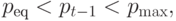 |
(
5.12)
|
где

из (5.2). Тогда закупка
спекулянтом в момент
t партии товара объемом

из (5.6) с целью продажи этой
партии в момент
t+1 по цене
pt+1 обеспечивает выполнение
условий (5.9), если
значение коэффициента

лежит в интервале
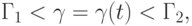 |
(
5.13)
|
где
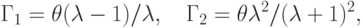 |
(
5.14)
|
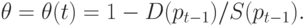 |
(
5.15)
|
Доказательство 1. Для выполнения входящего
в (5.9) неравенства pt<peq,
где, согласно (4.6) и (5.2),
 |
(
5.16)
|
необходимо и достаточно выполнения условия
D(pt)>D(peq).
Последнее условие в сочетании с равенствами (4.5) и (5.7) ведет к
соотношениям
Отсюда следует
неравенство
приводимое, с учетом (4.3), к виду
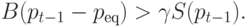 |
(
5.17)
|
Поскольку, согласно (4.1), (4.3), (5.15) и (5.16),
то требование (5.17) представимо в виде неравенства
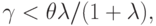 |
(
5.18)
|
которое заведомо выполняется при
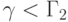
;
см. (5.13), (5.14).
При этом, согласно (5.12) и (5.15),
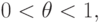 |
(
5.19)
|
поскольку
D(pt-1)<S(pt-1) при
peq<pt-1.
2. Из (4.1) и (5.7) вытекает,
что при pt-1>peq
![\begin{aligned}
&p_t=[Ap_{\max}-(1-\gamma)S(p_{t-1})]/A=\\
&=[D(p_{t-1})-S(p_{t-1})+\gamma S(p_{t-1})]/A+p_{t-1}=\\
&=\lambda (p_{t-1}-c)(\gamma-\theta)+p_{t-1}.\\
\end{aligned}](/sites/default/files/tex_cache/46f51d1378cb9b4f0ce6997985955e4a.png) |
(
5.20)
|
Отсюда следует, что для выполнения входящего в (5.9)
неравенства
pt>pmin=c должно выполняться условие
Это условие заведомо выполняется, если коэффициент

удовлетворяет левому неравенству из (5.13), поскольку
pt-1>c и,
согласно (5.19),
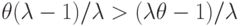
.
3.Условие pt+1>peq, входящее в (5.9),
равносильно отношению D(pt+1)<S(peq), которое,
учитывая (5.8), приводимо к виду:
или
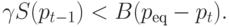 |
(
5.21)
|
Из (4.2), (4.6) и (5.20) следует, что
Подставляя правую часть этого равенства в (5.21), выводим,
что
pt+1>peq, если
Последнее условие эквивалентно требованию
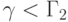
.
4. Условие pt+1<pt-1, входящее в (5.9) и
обеспечивающее "скрутку" паутины, равносильно неравенству D(pt+1)>D(pt-1), которое, согласно (5.8), можно
записать в виде:
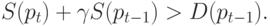 |
(
5.22)
|
Из (4.2), (5.2) и (5.20) выводим, что
Подставляя правую часть полученного выражения в (5.22), выводим
неравенство
для справедливости которого достаточно выполнения условия
Последнее условие заведомо выполняется при
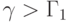
, где

из (5.14). В заключение отметим, что
интервал (5.13) не
пуст (т.е.
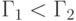
при значениях

из
диапазона (5.11).
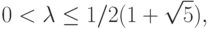
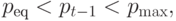
 из (5.2). Тогда закупка спекулянтом в момент t партии товара объемом
из (5.2). Тогда закупка спекулянтом в момент t партии товара объемом  из (5.6) с целью продажи этой
партии в момент t+1 по цене pt+1 обеспечивает выполнение
условий (5.9), если значение коэффициента
из (5.6) с целью продажи этой
партии в момент t+1 по цене pt+1 обеспечивает выполнение
условий (5.9), если значение коэффициента  лежит в интервале
лежит в интервале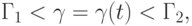
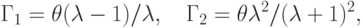
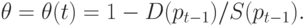

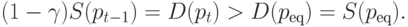

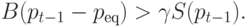
![\begin{aligned}
&p_{t-1}-p_\text{eq}=[\lambda (p_{t-1}-c)+(p_{\max}-p_{t-1})]/(1+\lambda)=\\
&\qquad\qquad=[S(p_{t-1})-D(p_{t-1})]/(A+B)=\theta S(p_{t-1})/(A+B),\\
\end{aligned}](/sites/default/files/tex_cache/894e5cc755c5a8cdade9652f816177fb.png)
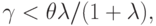
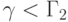 ;
см. (5.13), (5.14).
При этом, согласно (5.12) и (5.15),
;
см. (5.13), (5.14).
При этом, согласно (5.12) и (5.15),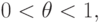
![\begin{aligned}
&p_t=[Ap_{\max}-(1-\gamma)S(p_{t-1})]/A=\\
&=[D(p_{t-1})-S(p_{t-1})+\gamma S(p_{t-1})]/A+p_{t-1}=\\
&=\lambda (p_{t-1}-c)(\gamma-\theta)+p_{t-1}.\\
\end{aligned}](/sites/default/files/tex_cache/46f51d1378cb9b4f0ce6997985955e4a.png)
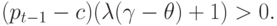
 удовлетворяет левому неравенству из (5.13), поскольку pt-1>c и,
согласно (5.19),
удовлетворяет левому неравенству из (5.13), поскольку pt-1>c и,
согласно (5.19), 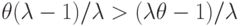 .
.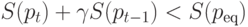
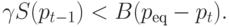
![p_\text{eq}-p_t=B[S(p_{t-1})-D(p_{t-1})-D(p_{t-1})]/A(A+B)-\gamma S(p_{t-1})/A.](/sites/default/files/tex_cache/f5ece351dbe73f67afe96402b7bb9a99.png)
![\gamma (\lambda +1)^2S(p_{t-1})<\lambda^2[S(p_{t-1})-D(p_{t-1})].](/sites/default/files/tex_cache/6266fc62527426cc3f156592313e6704.png)
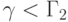 .
.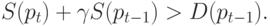
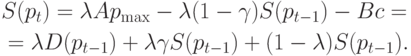
![(\lambda-1)[S(p_{t-1})-D(p_{t-1})]<\gamma (\lambda+1)S(p_{t-1}),](/sites/default/files/tex_cache/de393a6d280af1174ff32e0603c8cc8f.png)
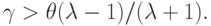
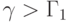 , где
, где  из (5.14). В заключение отметим, что интервал (5.13) не
пуст (т.е.
из (5.14). В заключение отметим, что интервал (5.13) не
пуст (т.е. 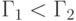 при значениях
при значениях  из
диапазона (5.11).
из
диапазона (5.11).
