|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Устойчивость и эффективность поведения сторон: совместимость свойств устойчивости и эффективности
Устойчивость и эффективность решений
Использование в рассмотренном выше примере оценок гарантированной эффективности стратегий (по отношению к возможным значениям неопределенного состояния природы) привело к тому, что проблема выбора стратегий
![x=x_1\in X=[0,1],\quad y=x_2\in Y=[0,1]](/sites/default/files/tex_cache/433809c3ee2b11d27963f876854d521a.png) |
( 3.1) |
Во-первых, игроки P1 и P2 не заинтересованы в отклонении от поведения, определяемого этими стратегиями, поскольку любые такие отклонения могут лишь уменьшить уровень полезности, гарантируемый им стратегиями
 |
( 3.2) |
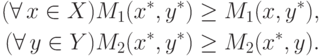 |
( 3.3) |
Определение 1.4 ( Равновесие по Нэшу ).
Пара стратегий (x*,y*) из множества  , удовлетворяющая
неравенствам (3.3) для платежных функций Mi(x,y), i=1,2
некоторой игры вида (1.16), называется устойчивой
стратегической точкой или стратегической
точкой равновесия (по Нэшу1Нэш Джон (р.1928) - американский экономист, лауреат Нобелевской премии (1994).
) в этой игре.
, удовлетворяющая
неравенствам (3.3) для платежных функций Mi(x,y), i=1,2
некоторой игры вида (1.16), называется устойчивой
стратегической точкой или стратегической
точкой равновесия (по Нэшу1Нэш Джон (р.1928) - американский экономист, лауреат Нобелевской премии (1994).
) в этой игре.
Второе важное свойство решения (3.2) - невозможность улучшить гарантируемые этим решением уровни полезности (2.12) одновременно для обоих игроков. Таким образом, если свойство (3.3) устойчивости решения определяет отсутствие у каждой из сторон P1 и P2 каких-либо индивидуальных мотивов для смены поведения, то обсуждаемое второе свойство указывает на отсутствие стимулов для смены поведения, реализуемой на основе каких-либо взаимных договоренностей между сторонами. Т.е. решение (3.2) оказывается неулучшаемым для обеих сторон.
Определение 1.5 ( Оптимальность по ) Парето2Парето Вильфредо (1848--1923) - итальянский экономист и социолог
.
Стратегии (x*,y*), составляющие пару из множества  , называются эффективным или оптимальным по Парето решением игры вида (1.16), если в
указанном множестве не существует другой пары
, называются эффективным или оптимальным по Парето решением игры вида (1.16), если в
указанном множестве не существует другой пары 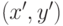 , такой, что соответствующие ей выигрыши Mi(x',y'), i=1,2, превышают платежи Mi(x*,y*), i=1,2, гарантируемые игрокам P1 и P2 стратегической парой (x*,y*). При этом
указанное превышение должно быть строгим хотя бы для одной из сторон. Таким образом,
стратегическая пара (x*,y*) является оптимальной по Парето,
если она удовлетворяет условиям
, такой, что соответствующие ей выигрыши Mi(x',y'), i=1,2, превышают платежи Mi(x*,y*), i=1,2, гарантируемые игрокам P1 и P2 стратегической парой (x*,y*). При этом
указанное превышение должно быть строгим хотя бы для одной из сторон. Таким образом,
стратегическая пара (x*,y*) является оптимальной по Парето,
если она удовлетворяет условиям
![\neg (\exists (x',y')\in X\times Y)[M_i(x',y')\ge M_i(x^*,y^*),\, i=1,2],](/sites/default/files/tex_cache/7a86f5a60a634afa4d7d5edf71c45281.png) |
( 3.4) |
Как уже было отмечено, в рамках описанной модели у игроков P1
и P2 нет ни индивидуальных, ни коллективных стимулов для
отклонения от
поведения, предписываемого эффективной парой стратегий (x*,y*), обладающей свойствами равновесия по Нэшу. В связи с
этим, стратегические пары (x*,y*) из множества  ,
обладающие указанными двумя свойствами, будем называть оптимальными решениями для игр вида (1.16).
Следует, однако, заметить, что описанные выше
свойства устойчивости и эффективности могут оказаться несовместимыми.
,
обладающие указанными двумя свойствами, будем называть оптимальными решениями для игр вида (1.16).
Следует, однако, заметить, что описанные выше
свойства устойчивости и эффективности могут оказаться несовместимыми.

