|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Математическая модель задачи выбора решений
Модель операции в нормальной форме
Непосредственное использование отношений R1 и R2, введенных выше для описания интересов сторон P1 и P2, предполагает задание всех пар (z1,z2), составляющих графики этих отношений. В случае, когда множество исходов Z содержит значительное число элементов, явное перечисление всех таких пар может оказаться слишком громоздким. Зачастую эту трудность можно преодолеть, вводя значительно более компактное описание отношений R1 и R2 с помощью вещественных функций H1(z) и H2(z), определенных на множестве исходов Z и неубывающих соответственно по предпочтениям R1 и R2.
Определение 1.1. Функция Hi(z), определенная на множестве исходов Z, называется неубывающей по нестрогому предпочтению Ri, если
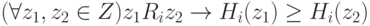 |
( 1.7) |
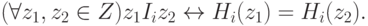 |
( 1.8) |
В случае, когда выполняются также условия
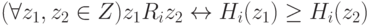 |
( 1.8) |
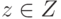 .
.Теорема 1.1. Функция Hi(z), неубывающая по полному квазипорядку Ri и удовлетворяющая условиям
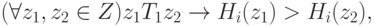 |
( 1.9) |
Доказательство. Свойство неубывания, включенное в условия теоремы, гарантирует
справедливость утверждения (1.7). Теперь допустим, что условия (1.8) не выполняются.
Т.е. во множестве  существует хотя бы одна пара (z1,z2), для которой справедливо неравенство
существует хотя бы одна пара (z1,z2), для которой справедливо неравенство
 |
( 1.10) |
В силу предположенной полноты квазипорядка Ri, это означает справедливость обратного отношения z2Riz1, которое, в соответствии с (1.2), эквивалентно условиям
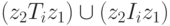 |
( 1.11) |
Согласно (1.3), истинность правого отношения в (1.11) противоречит принятому допущению о несправедливости z1Riz2. Допущение справедливости левого отношения в (1.11) ведет, согласно (1.9), к противоречию с (1.10). Таким образом, условия (1.8) необходимо выполняются для полного квазипорядка Ri.
Теорема 1.2. Любой полный квазипорядок Ri на конечном множестве Z может быть представлен неотрицательной вещественной функцией Hi(z), удовлетворяющей условиям (1.8).
Доказательство проведем путем построения функции Hi(z), 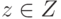 ,
удовлетворяющей указанным условиям. Пусть множество исходов Z0=Z
содержит N элементов. Выделим из множества Z0
подмножество Z1 всех исходов, удовлетворяющих условию:
,
удовлетворяющей указанным условиям. Пусть множество исходов Z0=Z
содержит N элементов. Выделим из множества Z0
подмножество Z1 всех исходов, удовлетворяющих условию:
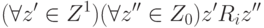
 . Положим Hi(z)=1,
. Положим Hi(z)=1, 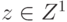 .
.Теперь построим подмножество Z2 множества Z1, удовлетворяющее условию:
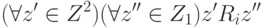
 .
Кроме того,
.
Кроме того,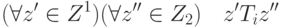
 ,
, 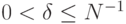 , и положим
, и положим  ,
, 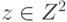 .
.Следуя описанной схеме, построим подмножество Zk+1
множества Zk,  , удовлетворяющее условию:
, удовлетворяющее условию:
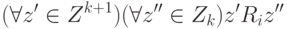
 . Кроме того,
. Кроме того,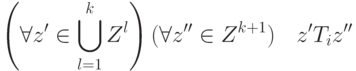
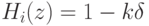 ,
, 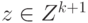 .
Тогда
.
Тогда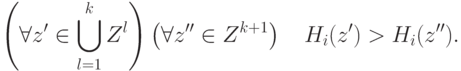
Описанный процесс построения множеств завершается при выполнении условия 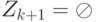 . При этом
. При этом
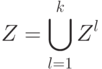
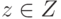 , причем, в
силу способа построения, функция Hi(z) является неубывающей по
предпочтению Ri. Таким образом, любой полный квазипорядок на
конечном множестве исходов, действительно, представим неотрицательной вещественной
функцией.
, причем, в
силу способа построения, функция Hi(z) является неубывающей по
предпочтению Ri. Таким образом, любой полный квазипорядок на
конечном множестве исходов, действительно, представим неотрицательной вещественной
функцией.Введение функций полезности H1(z) и H2(z)
(которые заведомо существуют в задачах с конечными множествами исходов, а также во многих
задачах, содержащих бесконечное число исходов), фактически позволяет
сторонам P1 и P2 иметь количественные оценки
степени достижимости их целей при завершении операции в некотором исходе 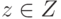 .
Указанные функции в сочетании с зависимостью (1.1) позволяют
ввести критерии эффективности
.
Указанные функции в сочетании с зависимостью (1.1) позволяют
ввести критерии эффективности
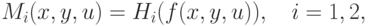 |
( 1.12) |
 и
и  , выбираемые сторонами P1 и P2, и реализующиеся в
ходе операции состояния природы
, выбираемые сторонами P1 и P2, и реализующиеся в
ходе операции состояния природы 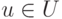 с теми уровнями полезности,
которые при этом достигаются.
с теми уровнями полезности,
которые при этом достигаются.Определение 1.2.
Построенная модель, где о стратегиях x, y сторон P1, P2 и о
состояниях природы u предполагается лишь то, что они являются
элементами заданных множеств X, Y и U, на прямом
произведении которых 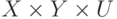 заданы критерии эффективности (1.12},
называется моделью операции в нормальной форме
заданы критерии эффективности (1.12},
называется моделью операции в нормальной форме
Как следует из определения, модель операции в нормальной форме, представляющая собой совокупность вида
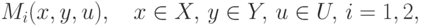 |
( 1.13) |
С одной стороны, введение критериев эффективности позволяет утверждать, что при заданной стратегии второй стороны и известном состоянии природы первая сторона заинтересована в выборе такой стратегии, которая максимизирует ее критерий, т.е. решает задачу
![M_{1}(x,y,u) \xrightarrow[x\in X]{} \max.](/sites/default/files/tex_cache/c781cf499831ba8f5ba633c7b5f2ad09.png) |
( 1.14) |
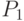 , как уже говорилось, не контролирует выбор
значений
, как уже говорилось, не контролирует выбор
значений  ,
,  и, более того, в общем
случае, может не знать эти значения в момент выбора своей стратегии.
и, более того, в общем
случае, может не знать эти значения в момент выбора своей стратегии.С другой стороны, сторона 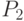 , выбирая свою стратегию
, выбирая свою стратегию  , стремится максимизировать свой
критерий эффективности, т.е. решает задачу
, стремится максимизировать свой
критерий эффективности, т.е. решает задачу
![M_2(x,y,u) \xrightarrow[y\in Y]{} \max.](/sites/default/files/tex_cache/2862d67c5ede937b657e6df72d6068ff.png) |
( 1.15) |

