|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
L. Сложность
L.2. Сложность проблемы
Теория сложности также рассматривает вопрос определения сложности проблемы до того, как алгоритм будет разработан. Чтобы оценить сложность проблем, могут использоваться две версии теоретических машин Тьюринга: детерминированная и недетерминированная. Недетерминированная машина может решить более трудные проблемы подбором первого решения и затем его проверкой.
Две широких категории
Теория сложности делит все проблемы на две широких категории: неразрешимые проблемы и разрешимые проблемы.
Неразрешимые проблемы
Неразрешимая проблема - проблема, для которой нет алгоритма решения. Алан Тьюринг показал, что известная проблема остановки неразрешима. Проблема остановки может быть просто изложена следующим образом: "Если дано описание алгоритма, входная информация и машина Тьюринга, то нет алгоритма, который мог бы определить, завершится ли когда-нибудь выполнение этого алгоритма (остановится ли в конечном счете машина)". В математике и информатике есть несколько неразрешимых проблем.
Разрешимые проблемы
Проблема разрешима, если может быть написан алгоритм для решения этой проблемы. Соответствующий алгоритм, однако, может быть или не быть выполнимым. Если проблема может быть решена с использованием алгоритма полиномиальной сложности или меньше, это называется разрешимой в разумное время.проблемой или просто разумной проблемой ( tractable problem). Если проблема может быть решена с применением алгоритма показательной сложности, ее называют неразрешимой в разумное время или тяжелой проблемой ( intractable problem).
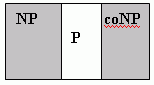
P, NP и coNP. Теория сложности делит разумные проблемы на три (возможно, накладывающиеся друг на друга) класса- P, NP и coNP . Как показано на рис. L.I, NP и coNP - перекрывающиеся, а P-класс находится на пересечении этих классов. Проблемы в классе P (P - polynomial) полиномиальные и могут быть решены детерминированной машиной Тьюринга в полиномиальное время. Проблемы NP класса ( NP - nondeterministic polynomial для недетерминированного полинома) могут быть решены недетерминированной машиной Тьюринга в полиномиальное время. Проблемы в классе coNP ( coNP - complementary nondeterministic polynomial - дополнительного недетерминированного полинома) - такие проблемы, которые могут быть решены недетерминированно путем дополнения маши ны Тьюринга. Например, проблема, которая решает, может ли целое число быть разложено на множители в два простых числа, есть дополнение проблемы, которая может решить, является ли число простым. Другими словами, утверждение "может быть разложен на множители" является эквивалентным доказательству "непростое число".
L.3. Вероятностные алгоритмы
Если проблема тяжелая, для ее решения мы можем найти вероятностный алгоритм. Хотя вероятностные алгоритмы не гарантируют, что решение свободно от ошибок, вероятность ошибки может быть сделана очень маленькой, с помощью повторения алгоритма с применением нескольких различных параметров. Вероятностные алгоритмы могут быть разделены на две категории: Монте-Карло и Лас-Вегас.
Алгоритм Монте-Карло
Алгоритм.Монте-Карло выдает решения "да/нет": выход алгоритма является или да, или нет.Алгоритм Монте-Карло, смещенный к ДА, дает результат ДА с вероятностью 1 (нет ошибки); он дает результат НЕТ с вероятностью e (возможная ошибка). Смещенный к НЕТ,.алгоритм Монте-Карло, выдаёт результат НЕТ с вероятностью 1 (нет ошибки); это дает результат ДА с вероятностью e (возможна ошибка). Мы рассмаривали вероятностные методыи в "A. ASCII" .
Алгоритм Монте-Карло, смещенный к ДА, может проверить, является ли целое число простым. Если алгоритм возвращает "простое" мы уверены, что целое число является простым; если он возвращает "составной объект", число может быть простым с очень небольшой вероятностью.
Алгоритм Лас-Вегаса
Алгоритм Лас-Вегаса - алгоритм, который либо успешен, либо ошибочен. Если он успешен, он всегда возвращает правильный ответ. Если он терпит неудачу, никто за это не отвечает.