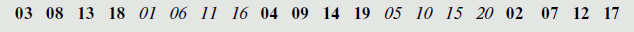|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Традиционные шифры с симметричным ключом
Объединение двух подходов
Современные шифры перестановки, чтобы достигнуть лучшего скремблирования, объединяют два подхода. Шифрование и дешифрование делается в три шага. Первый: текст пишется таблицей строка за строкой. Второй: делается перестановка, изменяя порядок следования столбцов. Третий: столбец за столбцом читается новая таблица. Первые и третьи шаги обеспечивают бесключевое глобальное изменение порядка следования; второй шаг обеспечивает блочную ключевую перестановку. Эти типы шифров упоминаются часто как ключевые шифры перестановки столбцов.
Пример 4.26
Предположим, что Алиса снова зашифровывает сообщение в примере 4.25, на сей раз используя объединенный подход. Шифрование и дешифрование показано на рис. 4.21.
Первая таблица, созданная Алисой, содержит исходный текст, записанный строка за строкой. Столбцы переставлены с использованием того же самого ключа, что и в предыдущем примере. Зашифрованный текст создан с помощью чтения второй таблицы столбец за столбцом. Боб делает те же самые три шага в обратном порядке. Он считывает таблицу зашифрованного текста столбец за столбцом в первую таблицу, переставляет столбцы, а затем читает вторую таблицу строку за строкой.
Ключи
В примере 4.27 единственный ключ использовался в двух направлениях для изменения порядка следования столбцов — вниз для шифрования, вверх для дешифрования. Обычно принято создавать два ключа для этого графического представления: один для шифрования и один для дешифрования. Ключи накапливаются в таблицах, имеющих один адрес (вход) для каждого столбца. Вход содержит исходный номер столбца — номер столбца пункта назначения, указывающий его положение от номера входа. Рисунок 4.22 показывает, как эти две таблицы могут быть созданы с помощью графического представления ключа.
Ключ шифрования — (3 1 4 5 2). Первый вход показывает, что столбец 3 (содержание) в источнике становится столбцом 1 (положение или индекс входа) в пункте назначения. Ключ дешифрования — (2 5 1 3 4). Первый вход показывает, что столбец 2 в источнике становится столбцом 1 в пункте назначения.
Как найти ключ дешифрования, если дан ключ шифрования или, наоборот, дан ключ дешифрации? Процесс может быть выполнен вручную за несколько шагов, как это показано на рис. 4.23. Сначала добавим индексы к таблице ключей, потом сделаем сдвиг в соответствии с полученным ключом, и, наконец, сортируем пару согласно индексу.
Использование матриц
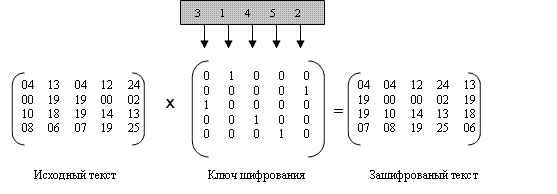
Мы можем использовать матрицы, чтобы показать процесс шифрования/дешифрования для шифра перестановки. Исходный текст и зашифрованный текст — матрица 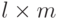 ., представляющая числовые значения символов; ключи — квадратные матрицы размера
., представляющая числовые значения символов; ключи — квадратные матрицы размера 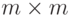 . В матрице перестановки каждая строка или столбец имеют строго одну единицу (1), и остальная часть значений — нули (0). Шифрование выполняется умножением матрицы исходного текста на ключевую матрицу, чтобы получить матрицу зашифрованного текста; дешифрование выполняется умножением зашифрованного текста на инверсию ключевой матрицы, после чего получаем исходный текст.
. В матрице перестановки каждая строка или столбец имеют строго одну единицу (1), и остальная часть значений — нули (0). Шифрование выполняется умножением матрицы исходного текста на ключевую матрицу, чтобы получить матрицу зашифрованного текста; дешифрование выполняется умножением зашифрованного текста на инверсию ключевой матрицы, после чего получаем исходный текст.
Очень интересно, что матрица дешифрования в этом случае, как и всегда, — инверсия матрицы шифрования. Однако нет никакой необходимости инвертировать матрицу — ключевая матрица шифрования может просто быть переставлена (сдвиг строк и столбцов), чтобы получить ключевую матрицу дешифрования.
Пример 4.27
Рисунок 4.24 показывает процесс шифрования. Умножение матрицы  исходного текста на ключевую матрицу шифрования
исходного текста на ключевую матрицу шифрования  дает матрицу зашифрованного текста
дает матрицу зашифрованного текста  . Матричная манипуляция требует изменения символов в примере 4.27 к их числовым значениям (от 00 до 25 ). Обратите внимание, что матричное умножение обеспечивает только перестановку столбцов; чтение и запись в матрицу должны быть обеспечены остальной частью алгоритма.
. Матричная манипуляция требует изменения символов в примере 4.27 к их числовым значениям (от 00 до 25 ). Обратите внимание, что матричное умножение обеспечивает только перестановку столбцов; чтение и запись в матрицу должны быть обеспечены остальной частью алгоритма.
Криптоанализ шифров перестановки
Шифры перестановки уязвимы к нескольким видам атак только для зашифрованного текста.
Статистическая атака
Шифр перестановки не изменяет частоту букв в зашифрованном тексте; он только переставляет буквы. Так что первая атака, которая может быть применена, - анализ частоты отдельной буквы. Этот метод может быть полезен, если длина зашифрованного текста достаточно большая. Мы такую атаку рассматривали раньше. Однако шифры перестановки не сохраняют частоту пар и триграмм. Это означает, что Ева не может использовать такие инструментальные средства. Фактически, если шифр не сохраняет частоту пар и триграмм, но сохраняет частоту отдельных букв, то вероятнее всего, что это шифр перестановки.
Атака грубой силы
Ева, чтобы расшифровать сообщение, может попробовать все возможные ключи. Однако число ключей может быть огромно 1! + 2! + 3! + … + L!, где L — длина зашифрованного текста. Лучший подход состоит в том, чтобы попробовать отгадать число столбцов. Ева знает, что число столбцов делится на L. Например, если длина шифра — 20 символов, то 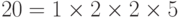 .
Это означает, что номером столбцов может быть комбинация этих коэффициентов (1, 2, 4, 5, 10, 20). Однако только один столбец и только одна строка — маловероятные варианты.
.
Это означает, что номером столбцов может быть комбинация этих коэффициентов (1, 2, 4, 5, 10, 20). Однако только один столбец и только одна строка — маловероятные варианты.
Пример 4.28
Предположим, что Ева перехватила сообщение зашифрованного текста "EEMYNTAACTTKONSHITZG". Длина сообщения L = 20, число столбцов может быть 1, 2, 4, 5, 10 или 20. Ева игнорирует первое значение, потому что это означает только один столбец и оно маловероятно.
a. Если число столбцов — 2, единственные две перестановки — (1,2) и (2, 1). Первое означает, что перестановки не было. Ева пробует вторую комбинацию. Она делит зашифрованный текст на модули по два символа "EE MY NT AA CT TK ON SH IT ZG". Затем она пробует переставлять каждый модуль из них, получая текст "ee ym nt aa tc kt no hs ti gz", который не имеет смысла.
b. Если номер столбцов — 4, тогда имеется 4! = 24 перестановки. Первая перестановка (1 2 3 4) означает, что не было никакой перестановки. Ева должна попробовать остальные. После испытания всех 23 возможностей Ева находит, что никакой исходный текст при таких перестановках не имеет смысла.
c. Если число столбцов — 5, тогда есть 5! = 120 перестановок. Первая (1 2 3 4 5) означает отсутствие перестановки. Ева должна попробовать остальные. Перестановка (2 5 13 4) приносит плоды — исходный текст "enemyattackstonightz", который имеет смысл после удаления фиктивной буквы z и добавления пробелов.
Атака по образцу
Другая атака шифра перестановки может быть названа атакой по образцу. Зашифрованный текст, созданный с помощью ключевого шифра перестановки, имеет некоторые повторяющиеся образцы. Следующий пример показывает зашифрованный текст, относительно которого известно, что каждый символ в зашифрованном тексте в примере 4.28 получается из исходного текста по следующему правилу:
1 -й символ в зашифрованном тексте получается из 3 -го символа исходного текста. 2 -й символ в зашифрованном тексте получается из 8 -го символа исходного текста. 20 -й символ в зашифрованном тексте получается из 17 -го символа исходного текста, и так далее. У нас имеются образцы в вышеупомянутом списке. Мы имеем пять групп: (3, 8, 13, 18), (1, 6, 11, 16), (4, 9, 14, 19), (5, 10, 15, 20) и (2, 7, 12, 17). Во всех группах разность между двумя смежными номерами — 5. Эта регулярность может использоваться криптоаналитиком, чтобы взломать шифр. Если Ева знает или может предположить число столбцов (в этом случае оно равняется 5 ), она может преобразовать зашифрованный текст в группы по четыре символа. Перестановка групп может обеспечить ключ к нахождению исходного текста.
Шифры c двойной перестановкой
Шифры с двойной перестановкой могут затруднить работу криптоаналитика. Примером такого шифра было бы повторение дважды алгоритма, используемого для шифрования и дешифрования в примере 4.26. На каждом шаге может применяться различный ключ, но обычно ключ используется один и тот же.
Пример 4.29
Повторим пример 4.26, где использована двойная перестановка. Рисунок 4.25 показывает процесс.
Хотя криптоаналитик может еще использовать частоту появления отдельного символа для статистической атаки на зашифрованный текст, атака по образцу теперь затруднена.
13 16 05 07 03 06 10 20 18 04 10 12 01 09 15 17 08 11 19 02
Сравнив приведенный текст и результат примера 4.28, мы видим, что теперь нет повторяющихся образцов. Двойная перестановка удалила ту регулярность, что мы имели раньше.