|
Хотелось бы иметь возможность читать текст сносок при использовании режима "Версия для печати" |
Проектирование реляционных баз данных на основе принципов нормализации: дальнейшая нормализация
Аномалии, вызываемые наличием зависимости проекции/соединения
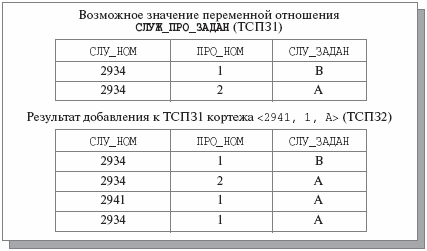
В переменной отношения СЛУЖ_ПРО_ЗАДАН выполняется PJD * ({СЛУ_НОМ, ПРО_НОМ}, {ПРО_НОМ, СЛУ_ЗАДАН}, {СЛУ_НОМ, СЛУ_ЗАДАН}). Наличие такой PJD обеспечивает возможность декомпозиции отношения на три проекции, но возникает вопрос, зачем это нужно? Чем плохо исходное отношение СЛУЖ_ПРО_ЗАДАН? Ответ обычный: этому отношению свойственны аномалии обновления. Для примера предположим, что значением СЛУЖ_ПРО_ЗАДАН является отношение, показанное на рис. 8.4.
-
Добавление кортежей. Если к ТСПЗ1 (рис. 8.4) добавляется кортеж <2941, 1, A>, то должен быть добавлен и кортеж <2934, 1, A>. Действительно, в теле отношения появятся кортежи <2934, 1, B>, <2941, 1, A> и <2934, 2, A>. Ограничение целостности требует включения и кортежа <2934, 1, A>. Интересно, что добавление кортежа <2934, 1, A> не нарушает ограничение целостности и, тем самым, не требует добавления кортежа <2941, 1, A>.
- Удаление кортежа. Если из ТСПЗ2 удаляется кортеж <2934, 1, A>, то должен быть удален и кортеж <2941, 1, A>, поскольку в соответствии с ограничением целостности наличие второго кортежа означает наличие первого. Интересно, что удаление кортежа <2941, 1, A> не нарушает ограничения целостности и не требует дополнительных удалений.
Устранение аномалий обновления в 3-декомпозиции
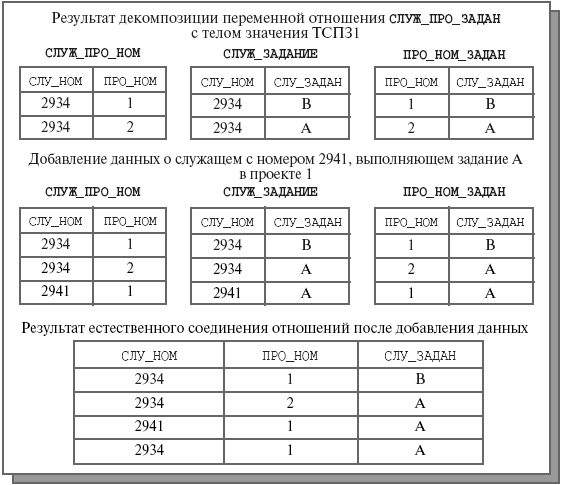
После выполнения декомпозиции трудности с обновлением автоматически снимаются. Действительно, декомпозируем отношение СЛУЖ_ПРО_ЗАДАН на три отношения: СЛУЖ_ПРО_НОМ {СЛУ_НОМ, ПРО_НОМ}, СЛУЖ_ЗАДАНИЕ {СЛУ_НОМ, СЛУ_ЗАДАН} и ПРО_НОМ_ЗАДАН {ПРО_НОМ, СЛУ_ЗАДАН}. Результат декомпозиции значения переменной отношения СЛУЖ_ПРО_ЗАДАН с телом ТСПЗ1 показан в верхней части рис. 8.5.
Теперь если мы хотим добавить данные о служащем с номером 2941, выполняющем задание A в проекте 1, то, естественно, вставим кортеж <2941, 1> в отношение СЛУЖ_ПРО_НОМ, кортеж <2941, A> в отношение СЛУЖ_ЗАДАНИЕ и кортеж <1, A> в отношение ПРО_НОМ-ЗАДАН. Результат этих операций показан в средней части рис. 8.5.
Но если выполнить естественное соединение декомпозированных отношений с телами, полученными после добавления данных о служащем с номером 2941, выполняющем задание A в проекте 1, то будет получено значение-отношение с заголовком отношения СЛУЖ_ПРО_ЗАДАН и телом ТСПЗ2 (нижняя часть рис. 8.5). Тем самым, проведенная декомпозиция позволила избежать сложностей при выполнении добавления кортежей с получением корректных результатов.
Аналогично можно проиллюстрировать простоту и корректность операций удаления кортежей.
Пятая нормальная форма
Отношения СЛУЖ_ПРО_НОМ, СЛУЖ_ЗАДАНИЕ и ПРО_НОМ_ЗАДАН находятся в пятой нормальной форме, но, прежде чем привести ее определение, нам требуется ввести еще два важных понятия.
В переменной отношения r PJD *( A, B, …, Z) называется подразумеваемой возможными ключами в том и только в том случае, когда каждый составной атрибут A, B, …, Z является суперключом r, т. е. включает хотя бы один возможный ключ r .
В переменной отношения r зависимость проекции/соединения *(A, B, …, Z) называется тривиальной, если хотя бы один из составных атрибутов A, B, …, Z совпадает с заголовком r .
Легко убедиться, что нетривиальные PJD, подразумеваемые возможными ключами, существуют во всех отношениях с арностью, большей двух, первичный ключ которых не совпадает с заголовком отношения. Например, если в отношении СЛУЖ_ПРО_ЗАДАН атрибут СЛУ_НОМ является первичным ключом, то, очевидно, имеется PJD *({СЛУ_НОМ, ПРО_НОМ}, {СЛУ_НОМ, СЛУ_ЗАДАН}) (это следует из теоремы Хита). Но такие зависимости проекции/соединения неинтересны с точки зрения проектирования базы данных, поскольку не порождают аномалии обновления. Поэтому общепринятое определение пятой нормальной формы выглядит следующим образом.
Переменная отношения r находится в пятой нормальной форме, или в нормальной форме проекции/соединения ( 5NF, или PJ/NF – Project-Join Normal Form ) в том и только в том случае, когда каждая нетривиальная PJD в r подразумевается возможными ключами r .
Таким образом, чтобы распознать, что данная переменная отношения r находится в 5NF, необходимо знать все возможные ключи r и все PJD этой переменной отношения. Обнаружение всех зависимостей соединения является нетривиальной задачей, и для ее решения нет общих методов. Поэтому на практике проектирование реляционных баз методом нормализации обычно завершается после достижения 4NF, и отношения, находящиеся в 4NF, как правило, находятся и в 5NF. Зачем же тогда была введена эта туманная и труднодостижимая пятая нормальная форма?
Ответ на этот естественный вопрос состоит в том, что 5NF является "окончательной" нормальной формой, которой можно достичь в процессе нормализации на основе проекций. " Окончательность " понимается в том смысле, что у отношения, находящегося в 5NF, отсутствуют аномалии обновлений, которые можно было бы устранить путем его декомпозиции. Другими словами, такие отношения далее нормализовать бессмысленно.