|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Принципы построения блочных шифров с закрытым ключом
Операции, используемые в блочных алгоритмах симметричного шифрования
Рассмотрим операции, используемые в большинстве алгоритмов симметричного шифрования. Будем при этом помнить, что рассматриваемые операции применяются к двоичным данным. Любая информация, например, изображения или текст, могут быть представлены в двоичном виде. Благодаря этому при шифровании не приходится задумываться о смысле передаваемых сообщений.
Одна из часто используемых операций – операция побитового сложения по модулю 2, обозначаемая XOR или  . Принципы выполнения этой операции подробно рассмотрены в
"Простейшие методы шифрования с закрытым ключом"
. При сложении по модулю 2 операнды обрабатываются поразрядно. В разряде результата ставится единица, если в соответствующих разрядах операндов присутствует нечетное число единиц. Например, сложим по модулю 2 два 16-разрядных числа:
. Принципы выполнения этой операции подробно рассмотрены в
"Простейшие методы шифрования с закрытым ключом"
. При сложении по модулю 2 операнды обрабатываются поразрядно. В разряде результата ставится единица, если в соответствующих разрядах операндов присутствует нечетное число единиц. Например, сложим по модулю 2 два 16-разрядных числа:
Эта операция имеет очень удобное свойство: вычитание по модулю два есть то же самое, что и сложение, поэтому один из операндов может быть получен путем прибавления к сумме другого операнда.
Также в блочных алгоритмах шифрования широко используется операция сложения по модулю 232 или по модулю 216. Эта операция представляет собой обыкновенное сложение двоичных чисел без учета переноса в старший 32-й или 16-й разряд результата. Например, сложим по модулю 216 два 16-разрядных числа:
Перенос из 15-го разряда, обозначенный в примере как единица в скобках, дальше не используется и поэтому отбрасывается.
Циклический сдвиг передвигает цепочку бит на некоторое число разрядов влево или вправо. Двоичное число при выполнении операции сдвига напоминает длинную гусеницу, выползающую с одной стороны туннеля и заползающую с другой. При циклическом сдвиге влево биты, выходящие слева за разрядную сетку дописываются справа на освободившиеся места. При циклическом сдвиге вправо все биты передвигаются цепочкой вправо, а те, которым не хватает места, переносятся в хвост цепочки. Например, выполним циклический сдвиг двоичного числа влево на 3 разряда. Для этого будем 3 раза переписывать двоичные цифры, каждый раз смещая их влево на 1 разряд и перенося знаки, выходящие из пятнадцатого разряда на место нулевого.
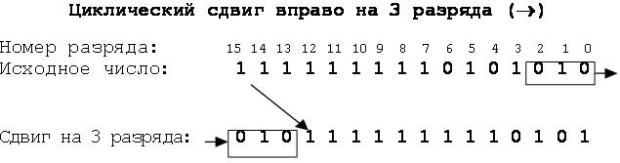
Аналогично выполняется и циклический сдвиг вправо. Например, при сдвиге вправо на 3 разряда нулевой, первый и второй биты исходного числа выходят из разрядной сетки и запоминаются, все остальные биты перемещаются вправо на 3 позиции, затем запомненные цифры записываются на тринадцатое, четырнадцатое и пятнадцатое места.
При выполнении табличной подстановки группа битов отображается в другую группу битов. При этой операции один блок двоичных данных заменяется по определенному правилу или таблице другим блоком. Например, можно заменять каждую группу из трех двоичных цифр другой группой из трех цифр по следующей таблице:
Если каждое значение, записанное в столбцах "Вход" и "Выход" записать не в двоичном, а в десятичном виде, то ту же самую таблицу замен можно будет записать более кратко, например, так:
0->3, 1->5, 2->0, 3->7, 4->2, 5->6, 6->1, 7->4
Первая цифра в такой записи представляет значение на входе, а вторая – на выходе. Если значения входов упорядочены по возрастанию в обычном порядке, то можно вообще не писать первую цифру, а записать только соответствующие значения выходов:
3, 5, 0, 7, 2, 6, 1, 4.
То есть в качестве замены для значения 3-битового блока выбирается элемент из таблицы замен с порядковым номером, равным значению заменяемого блока.
Если необходимо заменять группы из четырех двоичных цифр, то таблица замен должна содержать уже 16 значений. В общем случае для n-битовых блоков таблица замен должна содержать 2n элементов.
Табличную подстановку в литературе иногда называют заменой с использованием S-блоков или S-box. (Буква S взята от английского слова substitution – подстановка).
С помощью операции перемещения биты сообщения переупорядочиваются. Перемещение называют также permutation или P-блоком.
Структура блочного алгоритма симметричного шифрования
Таким образом, в алгоритмах симметричного шифрования часто используются операции сложения по модулю 2, сложения по модулю 216 или 232, циклического сдвига, замены и перестановки.
Эти операции циклически повторяются в алгоритме N раз, образуя так называемые раунды или шаги. Исходными данными для каждого раунда являются выход предыдущего раунда и ключ, который получен по определенному алгоритму из общего ключа шифрования K. Ключ раунда называется подключом Кi. В результате блочный алгоритм шифрования может быть представлен следующим образом ( рис. 3.1).
Блочные алгоритмы шифрования применяются к двоичным данным. В общем случае процедура блочного шифрования преобразовывает n-битный блок открытого текста в k-битный блок зашифрованного текста. Число блоков длины n равно 2n. Для того чтобы преобразование было обратимым, каждый из таких блоков должен преобразовываться в свой уникальный блок зашифрованного текста. Длина блока всегда выбирается равной степени двойки, например, 64, 128, 256 бит.