Управление риском
PERT и PERT-моделирование
PERT - метод оценки и проверки программ
В 1958 г. Особый отдел Военно-морского флота и консалтинговая фирма Booze, Allen and Hamilton создали PERT (метод оценки и проверки программ) с целью разработки графика для более чем 3300 подрядчиков, работающих над проектом подводной лодки Поларис, для решения проблемы неопределенности в расчетах времени выполнения работ.
PERT почти полностью совпадает с методом критического пути (СРМ), за исключением того, что PERT считает, что продолжительность каждой операции имеет пределы, которые исходят из статистического распределения.
PERT использует 3 оценки расчета времени для каждой операции:
- оптимистическое (наилучшее);
- средний показатель;
- пессимистическое (наихудшее).
Разработчики PERT для выражения продолжительности операции решили избрать аппроксимацию бета-распределения.
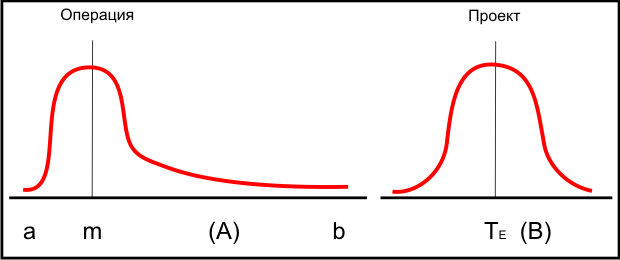
На рис. 5.2(А) представлено бета-распределение для продолжительности операции, отклоняющееся вправо, и оно представляет собой работу, которая имеет тенденцию отставать от графика.
Распределение продолжительности проекта показано в симметрии на рис. 5-2 (В).
Распределение проекта представляет собой сумму средневзвешенных показателей операций на критическом пути.
Средневзвешенное время операции рассчитывается по следующей формуле:
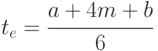 |
( 5.1) |
где te - средневзвешенное время операции;
а - оптимистическое время операции (1 шанс из 100, что при нормальных условиях операция будет закончена раньше срока);
b - пессимистическое время операции (1 шанс из 100, что при нормальных условиях операция будет закончена позже срока);
m - наиболее вероятное время операции.
Среднее (детерминистическое) значение накладывают на сеть проекта, как и при использовании СРМ, и затем рассчитывают раннее, позднее, резервное и время завершения проектных работ, как они указаны в СРМ.
Отклонения в оценках времени операции определяются при помощи следующих уравнений. Уравнение 5.2 представляет стандартное отклонение для операции.
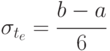 |
( 5.2) |
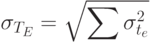 |
( 5.3) |
Уравнение 5.3 представляет стандартное отклонение для проекта.
Эта сумма включает в себя только виды операций на критическом или проверенном пути.
Средняя продолжительность проекта ( ТЕ ) - это сумма всех средних показателей времени, отведенных на выполнение операций по критическому пути (сумма от te ), и она следует нормальному распределению.
Зная среднюю продолжительность проекта и дисперсии (среднего отклонения) операций, можно с помощью статистических таблиц рассчитать выполнение проекта (или сегмента проекта) к конкретному времени.
Уравнение 5.4 используется для расчета величины Z, приводимой в статистических таблицах ( Z - количество стандартных отклонений от средней величины):
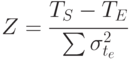 |
( 5.4) |
где ТЕ - продолжительность критического пути;
TS - продолжительность работы по графику;
Z - вероятность (выполнения графика), определенная по статистической табл. 5.6.
Гипотетический пример использования метода PERT
Продолжительность операций и значение среднего отклонения представлены на табл. 5.5.
| Операция | a | m | b | ТЕ | квадрат среднего отклонения |
|---|---|---|---|---|---|
| 1-2 | 17 | 29 | 47 | 30 | 25 |
| 2-3 | 6 | 12 | 24 | 13 | 9 |
| 2-4 | 16 | 19 | 28 | 20 | 4 |
| 3-5 | 13 | 16 | 19 | 16 | 1 |
| 4-5 | 2 | 5 | 14 | 6 | 4 |
| 5-6 | 2 | 5 | 8 | 5 | 1 |
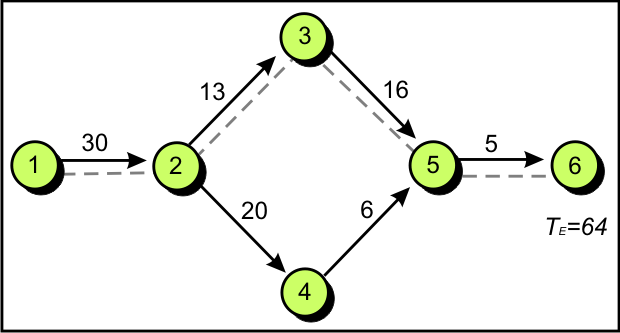
Сеть проекта представлена на рис. 5.3.
Прогнозируемый срок работы ( ТЕ ) представлен 64 единицами времени;
Критический путь - 1, 2, 3, 5, 6.
Имея эту информацию и используя стандартные статистические методы, можно легко рассчитать вероятность выполнения проекта к конкретному времени.
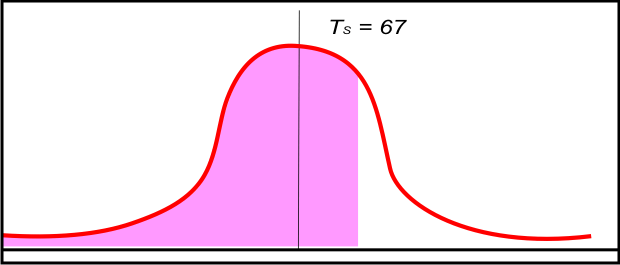
Например, какова вероятность завершения работы над проектом до указанного в графике времени ( Ts ) из 67?
Обычная кривая проекта будет такой как на рис. 5.4
Используя формулу для значения Z, можно рассчитать вероятность следующим образом:
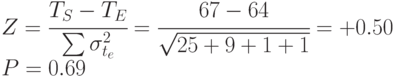
По данным табл. 5.6 значение Z + 0,5 дает вероятность 0,69, что означает 69%-ную вероятность завершения работы над проектом на 67-ю единицу времени или ранее.
| Величина Z | Вероятность | Величина Z | Вероятность |
|---|---|---|---|
| -2,0 | 0,02 | +2,0 | 0,98 |
| -1,5 | 0,07 | + 1,5 | 0,93 |
| -1,0 | 0,16 | +1,0 | 0,84 |
| -0,7 | 0,24 | +0,7 | 0,76 |
| -0,5 | 0,31 | +0,5 | 0,69 |
| -0.3 | 0,38 | +0,3 | 0,62 |
| -0,1 | 0,36 | +0,1 | 0,54 |
Вероятность выполнения проекта к периоду времени 60 рассчитывается следующим образом:
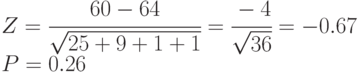
По табл. 5.6 значение Z - 0,67 дает вероятность 0,26, что означает около 26% вероятности завершения работы над проектом на 60-ю единицу времени или ранее.
Аналогичный способ расчетов можно использовать для любого пути или участка пути в сети.
PERT-моделирование
Для этой методики необходима компьютерная программа, моделирующая отпущенные на проект время, затраты и/или наличие ресурсов с использованием метода Monte Carlo Technique.
Решения по сохранению или переадресации рисков принимаются с помощью информации, полученной в результате моделирования времени, затрат и ресурсов.
PERT и моделирование PERT применяются в проектах чрезвычайной важности, которым присуща большая степень неопределенности и где в достаточной степени точно можно рассчитать время на выполнение операций. -
Вопросы для повторения
- Если проект тщательно спланирован, проектные риски можно/нельзя устранить. Объясните.
- Возможность рисков и соответственный им рост затрат меняются на протяжении жизненного цикла проекта, Каково значение этого явления для управляющего проектом?
- Объясните, в чем разница между сметными резервами и резервами управления.
- Как связаны между собой структура распределения работы по этапам проекта и контроль над изменениями?
- Каковы возможные последствия неприменения процесса контроля над изменениями? Почему?
- Каким образом информация по PERT отличается от информации по СРМ?
- Как с помощью PERT рассчитать вероятность конкретной продолжительности выполнения проекта? Какие подходы лежат в основе этого метода?
- Почему на практике метод PERT используется редко?