|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Проблемы повышения эффективности функционирования производственно-корпоративных структур (ПКС)
Далее необходимо сравнить полученное значение с допустимым отклонением ожидаемой вероятности  .
.
Если при 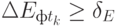
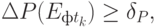 то данный этап проходит нормально, то есть финансово-экономическая эффективность выше критического значения, вероятность ее достижения достаточно высока. В этом случае следует перейти к следующему этапу проекта.
то данный этап проходит нормально, то есть финансово-экономическая эффективность выше критического значения, вероятность ее достижения достаточно высока. В этом случае следует перейти к следующему этапу проекта.
Если при 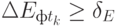
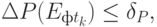 то на данном этапе реализации проекта достижение удовлетворительного значения финансово-экономической эффективности носит сомнительный характер. Поэтому следует пересмотреть механизм учета внешних факторов и способов достижения поставленных целей.
то на данном этапе реализации проекта достижение удовлетворительного значения финансово-экономической эффективности носит сомнительный характер. Поэтому следует пересмотреть механизм учета внешних факторов и способов достижения поставленных целей.
Учитывая изложенное, можно сделать вывод: в общем случае решение об интеграции в ПКС каждым из участников, как самостоятельным хозяйствующим субъектом, принимается самостоятельно, но зависит от принятия решений другими участниками, т. е. оптимальное значение целевой функции зависит от решений, принимаемых всеми остальными участниками. Поэтому решение задачи интеграции следует искать с помощью теории игр [14, 19, 29, 66]. Так как в рамках игры участники могут обсуждать свои стратегии, договариваться о совместных действиях и образовывать коалиции, то игру можно рассматривать как кооперативную, причем с побочными платежами, т. е. между игроками могут заключаться взаимообязывающие соглашения о стратегиях, а выигрыши (оптимизируемые величины - эффективности) могут перераспределяться между игроками. Такие игры можно анализировать с помощью характеристической функции игры, которая указывает максимальный гарантированный выигрыш для каждой коалиции. Если  - множество игроков (общее количество потенциальных участников ПКС), а
- множество игроков (общее количество потенциальных участников ПКС), а 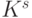 - подмножество множества
- подмножество множества  , отражающее количество участников при интеграции по форме
, отражающее количество участников при интеграции по форме  , то подмножество
, то подмножество  множества
множества 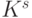 является коалицией, и характеристическую функцию можно записать в виде
является коалицией, и характеристическую функцию можно записать в виде 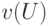 , где
, где 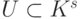 ,
,  . С помощью характеристической функции игру удобно представлять в нормализованной форме:
. С помощью характеристической функции игру удобно представлять в нормализованной форме:
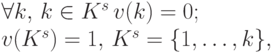
т. е. выигрыш самостоятельно действующего игрока равен нулю для всех игроков, выигрыш коалиции, включающей всех игроков, равен 1. Естественно, должно соблюдаться условие:  . В характеристической функции заложены переговорные процессы, механизмы выработки совместных стратегий, процессы образования коалиций.
. В характеристической функции заложены переговорные процессы, механизмы выработки совместных стратегий, процессы образования коалиций.
Обозначим вектор  -мерного пространства, который называется "дележом", через
-мерного пространства, который называется "дележом", через 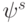 . Составляющими вектора будут выигрыши (эффективности) каждого участника при интеграции по варианту
. Составляющими вектора будут выигрыши (эффективности) каждого участника при интеграции по варианту  :
:
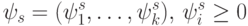
Зададим сильный критерий доминирования на множестве дележей с помощью ядра игры. Ядром (или С-ядром) называется множество всех недоминируемых дележей, то есть таких дележей 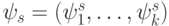 ,
), которые удовлетворяют условию:
,
), которые удовлетворяют условию:
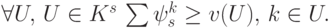
Это означает, что любая коалиция при данном дележе получает не меньше, чем могли бы получить в сумме все входящие в нее игроки. Указанное неравенство дает удобный способ нахождения ядра путем решения линейной системы неравенств. Решением системы является выпуклый многогранник в пространстве. Можно найти его крайние точки и описать любое решение, принадлежащее ядру, как взвешенную комбинацию крайних точек [14]. Ядро может содержать множество возможных дележей и представлять собой множество решений. Для того чтобы прийти к единственному решению, введем вектор Шепли - дележ, величина выигрышей в котором зависит от силы каждого игрока. Сила игрока рассчитывается, исходя из значения дополнительного выигрыша коалиции, когда данный игрок в нее войдет. Тогда выигрыш  -го участника составит:
-го участника составит:
![\psi_s^k =\sum{\mu(U)[v(U \cup \{k\}) -v(U) ]}, \, U \subset K](/sites/default/files/tex_cache/9cbd661677632589f8f55d7348bdc866.png)
где  - любое подмножество участников, не содержащее
- любое подмножество участников, не содержащее  -го участника,
-го участника,
 и
и 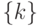 - то же подмножество, включающее
- то же подмножество, включающее  -го участника,
-го участника,
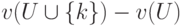 - взвешиваемые дополнительные выигрыши,
- взвешиваемые дополнительные выигрыши,
![\mu(U) = [u!(n - u -1)!]/n](/sites/default/files/tex_cache/e8b8235492e27460b6810863d69f1ab2.png) ! - взвешивающие множители,
! - взвешивающие множители,
 - количество участников в
- количество участников в  .
.
Взвешивающие множители представляют собой вероятности присоединения  -го игрока к коалиции
-го игрока к коалиции  . В данном случае взвешивающие множители рассчитаны исходя из того, что способы формирования коалиций, состоящих из
. В данном случае взвешивающие множители рассчитаны исходя из того, что способы формирования коалиций, состоящих из  участников, равновероятны.
участников, равновероятны.
Необходимо помнить, что выигрыш 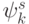 есть не что иное, как финансово-экономическая эффективность
есть не что иное, как финансово-экономическая эффективность 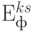 .
.
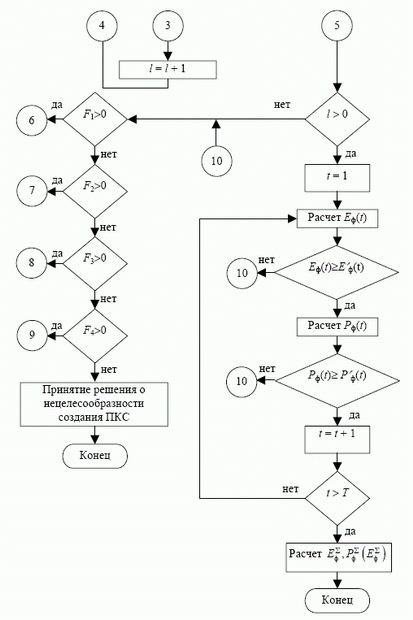
Разработка структуры и состава принципиальной структурно-функциональной блок-схемы организационно-экономического моделирования создания и эффективного функционирования ПКС.Структурно-функциональная блок-схема моделирования создания и эффективного функционирования ПКС отображена на рис. 1.15.
увеличить изображение
Рис. 1.15. Структурно-функциональная блок-схема моделирования создания и эффективного функционирования производственно-корпоративной системы (ПКС)
На первом этапе создания ПКС необходимо определить цели создания ПКС. В качестве основной цели эффективного функционирования ПКС можно взять финансово-экономическую эффективность 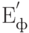 с минимально допустимой вероятностью ее достижения
с минимально допустимой вероятностью ее достижения 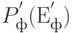 . Также необходимо сформировать массив факторов внешней среды
. Также необходимо сформировать массив факторов внешней среды  , влияющих на производственно-хозяйственную деятельность ПКС и ее участников. Достижение целей во многом регламентируется маркетинговой стратегией, в результате разработки которой устанавливаются пути достижения целей, вырабатываются критерии их достижения, определяются плановые финансово-экономические показатели, в том числе плановое значение эффективности и вероятности ее достижения, сроки
, влияющих на производственно-хозяйственную деятельность ПКС и ее участников. Достижение целей во многом регламентируется маркетинговой стратегией, в результате разработки которой устанавливаются пути достижения целей, вырабатываются критерии их достижения, определяются плановые финансово-экономические показатели, в том числе плановое значение эффективности и вероятности ее достижения, сроки  и этапы
и этапы  реализации проекта.
реализации проекта.
В соответствии с целями, путями их достижения, факторами внешней среды, характером деятельности ПКС, видами и размерами необходимых финансово-экономических показателей необходимо сформировать перечень K возможных участников с учетом их собственных существующих и возможно достижимых финансово-экономических показателей 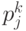 . Каждый из участников имеет собственную общую эффективность
. Каждый из участников имеет собственную общую эффективность 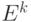 .
.
На следующем этапе просчитываются варианты интеграции предприятий из состава возможных участников.
Обозначим общее количество таких вариантов через  . По каждому варианту производится расчет финансово-экономической эффективности
. По каждому варианту производится расчет финансово-экономической эффективности 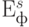 . Сначала определяются коэффициенты взаимовлияния внешних факторов и участников
. Сначала определяются коэффициенты взаимовлияния внешних факторов и участников 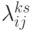 и коэффициенты взаимовлияния участников и ПКС
и коэффициенты взаимовлияния участников и ПКС 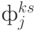 .
С учетом коэффициентов
.
С учетом коэффициентов 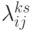 и
и 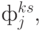 а также финансово-экономических показателей участников
а также финансово-экономических показателей участников 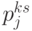 производится расчет финансово-экономической эффективности
производится расчет финансово-экономической эффективности 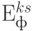
 -го участника по варианту интеграции
-го участника по варианту интеграции  :
:
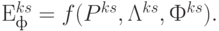
Затем производится расчет общей финансово-экономической эффективности ПКС 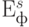 при интеграции участников по варианту
при интеграции участников по варианту  :
:

При этом следует учитывать, что в процессе взаимодействия эффективности участников 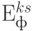 могут как увеличиваться, так и уменьшаться. В любом случае должно соблюдаться достаточное условие объединения участников:
могут как увеличиваться, так и уменьшаться. В любом случае должно соблюдаться достаточное условие объединения участников:
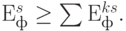
Далее определяется наибольшее на момент расчета значение финансово-экономической эффективности 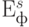 , для которого производится расчет вероятности
, для которого производится расчет вероятности  достижения указанного значения эффективности. Полученное значение вероятности
достижения указанного значения эффективности. Полученное значение вероятности 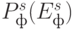 затем сверяется с минимально допустимым значением вероятности
затем сверяется с минимально допустимым значением вероятности 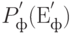 .
.
Чтобы установить положительный результат расчета вариантов финансово-экономической эффективности, вводится показатель  наличия приемлемых вариантов финансово-экономической эффективности
наличия приемлемых вариантов финансово-экономической эффективности 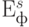 .
.
Если  , производится проверка возможности корректировки возможного состава участников
, производится проверка возможности корректировки возможного состава участников 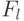 . В случае наличия указанной возможности, производится корректировка. Если состав участников корректировке не подлежит, то рассматривается возможность изменения стратегии создания и функционирования ПКС, плановых показателей, сроков реализации проекта
. В случае наличия указанной возможности, производится корректировка. Если состав участников корректировке не подлежит, то рассматривается возможность изменения стратегии создания и функционирования ПКС, плановых показателей, сроков реализации проекта 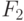 . В противном случае проверяется возможность произвести корректировку учета факторов внешней среды
. В противном случае проверяется возможность произвести корректировку учета факторов внешней среды 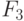 : уточнение и конкретизация известных факторов, возможности ввода дополнительных внешних факторов, ранее не учтенных. В некоторых случаях возможно воздействие на внешние факторы с целью их изменения в нужную сторону. При наличии указанных возможностей факторы внешней среды и их учет корректируются. Если возможности корректировки стратегии исчерпаны, а положительный результат финансово-экономической эффективности не получен, то рассматривается возможность корректировки целей организации и функционирования ПКС
: уточнение и конкретизация известных факторов, возможности ввода дополнительных внешних факторов, ранее не учтенных. В некоторых случаях возможно воздействие на внешние факторы с целью их изменения в нужную сторону. При наличии указанных возможностей факторы внешней среды и их учет корректируются. Если возможности корректировки стратегии исчерпаны, а положительный результат финансово-экономической эффективности не получен, то рассматривается возможность корректировки целей организации и функционирования ПКС 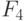 . При отсутствии указанной возможности принимается решение о нецелесообразности создания ПКС.
. При отсутствии указанной возможности принимается решение о нецелесообразности создания ПКС.
В том случае, когда приемлемые варианты значений финансово-экономической эффективности 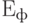 после завершения стадии проектирования ПКС существуют, то производится расчет
после завершения стадии проектирования ПКС существуют, то производится расчет 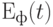 на каждом этапе
на каждом этапе  жизненного цикла реализации проекта. При этом также проверяется на допустимость вероятность достижения эффективности
жизненного цикла реализации проекта. При этом также проверяется на допустимость вероятность достижения эффективности 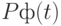 .
.
По завершении моделирования создания и эффективного функционирования ПКС производится расчет общей финансово-экономической эффективности от реализации проекта 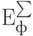 и вероятность ее достижения
и вероятность ее достижения 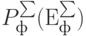 с учетом всех этапов.
с учетом всех этапов.