|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Шифрование, помехоустойчивое кодирование и сжатие информации
Минимальное расстояние между допустимыми словами кода с контролем по четности равно двум (из рис. 14.2 видно, что никакие два кодовых слова в рамочках не соединены линиями, то есть не являются соседними). Именно по этой причине одиночная ошибка в кодовом слове превращает это слово в недопустимое.
Платой за помехоустойчивость является необходимость увеличения длины слов по сравнению с обычным кодом. В данном примере только два разряда являются информационными. Это они образуют четыре разных слова. Третий разряд является контрольным и служит только для увеличения расстояния между допустимыми словами. В передаче информации контрольный разряд не участвует, так как является линейно зависимым от информационных. Код с контролем по четности, рассмотренный в качестве примера, позволяет обнаружить одиночные ошибки в блоках данных при передаче данных. Однако он не сможет обнаружить двукратные ошибки потому, что двукратная ошибка переводит кодовое слово через промежуток между допустимыми словами и превращает его в другое допустимое слово.
Таким образом, для того чтобы код приобрел способность к обнаружению и коррекции ошибок, необходимо отказаться от его безызбыточности. Для этого и разделяют всё множество возможных комбинаций двоичных символов на два подмножества: допустимых кодовых слов и недопустимых. Разбиение осуществляется таким образом, чтобы увеличить минимальное кодовое расстояние между допустимыми словами. В этом случае любая однократная ошибка превращает допустимое кодовое слово в недопустимое, что позволяет её обнаружить.
Естественно, что введение дополнительных контрольных разрядов увеличивает затраты на хранение или передачу кодированной информации. При этом фактический объем полезной информации остается неизменным. В этом случае можно говорить об избыточности помехоустойчивого кода, которую формально можно определить как отношение числа контрольных разрядов к общему числу разрядов кодового слова.
Мы уже отмечали, что контрольные разряды не передают информацию и в этом смысле бесполезны. Относительное число контрольных разрядов называется избыточностью Q помехоустойчивого кода

где n – общее число двоичных разрядов в блоке, а k – число контрольных разрядов.
Например, избыточность рассмотренного трехразрядного кода с контролем по четности составляет:
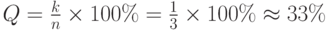
Избыточность является важной характеристикой кода, причем чрезмерное увеличение избыточности нежелательно. Важной задачей теории информации является синтез кодов с минимальной избыточностью, обеспечивающих заданную обнаруживающую и корректирующую способность.
В качестве иллюстрирующего примера рассмотрим один из простейших кодов, позволяющих обнаруживать и исправлять однократные ошибки – код Хэмминга. Кодовое слово длиной n содержит k информационных и m контрольных разрядов. Коррекция искаженного i-го разряда заключается в сложении (по модулю 2) принятого кодового слова с вектором вида 0…010…0, содержащем единицу в i-ом разряде.
Для n-разрядного кодового слова существует n таких векторов, соответствующих однократным ошибкам, и один нулевой вектор, соответствующий случаю приема слова без ошибок. Таким образом, m контрольных разрядов должны обеспечивать формирование n + 1 вектора ошибки, то есть должно выполняться неравенство  . В результате получается (2m-1, 2m-1-m) код, называемый кодом Хэмминга.
. В результате получается (2m-1, 2m-1-m) код, называемый кодом Хэмминга.
Простейший нетривиальный случай, соответствующий m=3, образует (7,4)-код, который можно синтезировать следующим образом. Сопоставим каждому вектору ошибки порядковый номер – синдром ( таблица 14.1). При этом нулевому вектору ошибки соответствует нулевой синдром.
| a6 | a5 | a4 | a3 | a2 | a1 | a0 | s2 | s1 | s0 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Рассматривая функции si как свертку по модулю 2 разрядов кодовых слов, получим:

Функции si должны обращаться в единицу при наличии ошибки в одном из образующих их разрядов, и в ноль – при отсутствии ошибок. Обеспечение этого требования возможно лишь при условии, что часть разрядов формируется специальным образом. В частности, разряды a0, a1, a2 можно рассматривать как свертку по модулю 2 остальных разрядов, участвующих в соответствующих уравнениях:

Найденные зависимости позволяют генерировать кодовые слова по заданным информационным, а также вычислять синдромы для принятых кодовых слов.
Допустим, исходное информационное слово равно 1101, то есть a6=1, a5=1, a4=1, a3=1. Для преобразования его в допустимое кодовое слово помехоустойчивого (7,4) -кода Хэмминга рассчитаем контрольные разряды по найденным выше зависимостям. В частности,

Таким образом, с учетом контрольных разрядов кодовое слово будет равно 1101001.
Если в процессе передачи или хранения слово осталось неискаженным, то его синдром s0…s2 будет соответственно равен: 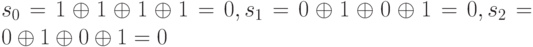 ,. Синдром, состоящий из одних нулей, указывает на отсутствие ошибки и соответствует нулевому вектору ошибки.
,. Синдром, состоящий из одних нулей, указывает на отсутствие ошибки и соответствует нулевому вектору ошибки.
Предположим, что в процессе передачи или хранения в результате воздействия внешних факторов оказался искаженным отдельный разряд кодового слова. Например, вместо слова 1101001 было принято слово 1001001. В этом случае синдром окажется отличным от нуля: s0…s2 будет соответственно равен: 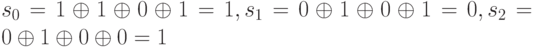 Синдром 101 соответствует вектору ошибки 0100000, при этом единица указывает на разряд, в котором эта ошибка произошла. Для ее коррекции достаточно сложить по модулю 2 принятое искаженное кодовое слово с вектором ошибки.
Синдром 101 соответствует вектору ошибки 0100000, при этом единица указывает на разряд, в котором эта ошибка произошла. Для ее коррекции достаточно сложить по модулю 2 принятое искаженное кодовое слово с вектором ошибки.
Рассчитаем избыточность (7,4) -кода Хэмминга:

Это очень большое значение. На практике часто применяются существенно более сложные коды, обеспечивающие лучшие характеристики помехоустойчивости при меньшей избыточности.

