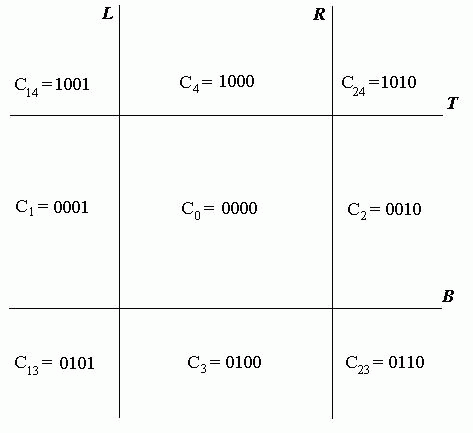Инспектор
Вы можете этот курс.
Опубликован: 20.10.2007 | Уровень: специалист | Доступ: платный
Лекция 5:
Отсечение (клиппирование) геометрических примитивов
Аннотация: Алгоритм деления отрезка пополам. Коды Сазерланда — Коэна. Клиппирование многоугольников. Штрихование многоугольной области. Переход к трехмерному клиппированию пирамидой видимости
Ключевые слова: плоскость, прямоугольник, отрезок, алгоритм, бит, прямой, таблица истинности, Произведение, значение, ПО, ребро, поиск, пересечение, блок-схема, определение, анализ, функция, операции, длина, множества, вектор, скалярное произведение векторов, скалярное произведение, место, расстояние, список, векторное произведение
В компьютерной графике часто приходится решать задачу выделения некоторой области изображаемой сцены, причем задача эта может решаться как в применении к плоской области (если сцена уже спроецирована на картинную плоскость), так и к трехмерной. Алгоритмы отсечения применяются для удаления невидимых поверхностей и линий, для построения теней, при формировании текстур. Отсекаемая область может быть как правильной формы (прямоугольник или параллелепипед со сторонами, параллельными осям координат или координатным плоскостям), так и неправильной (произвольный многоугольник или многогранник). Для того чтобы эти алгоритмы можно было использовать в задачах изображения динамичных сцен, они должны быть эффективными в отношении времени вычислений. Мы рассмотрим несколько наиболее часто применяемых алгоритмов.
Алгоритм Сазерленда-Коэна отсечения прямоугольной областью
Рассмотрим плоскую сцену, состоящую из отрезков различной длины и
направлений, в которой надо выделить часть, находящуюся внутри
прямоугольника. Прямоугольник задан списком ребер: <top>, <bottom>,
<left>, <right>, отрезки также задаются координатами концевых точек.
Область, отсекаемая окном (с учетом его границы), состоит из точек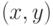 
,
удовлетворяющих соотношениям
 |
( 5.1) |
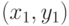и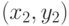 
. Первый шаг алгоритма нацелен
на то, чтобы выявить полностью видимые и полностью невидимые отрезки.
Отрезок целиком принадлежит выделяемой (клиппируемой) области, если
оба его конца удовлетворяют условиям (5.1).
Отрезок полностью невидим, если оба его конца лежат
- справа от ребра
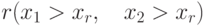; - слева от ребра
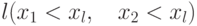; - снизу от ребра
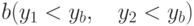; - сверху от ребра
.
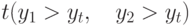Во всех остальных случаях отрезок может (но не обязан) пересекать прямоугольное окно.
Для выполнения анализа полной видимости или невидимости отрезка
А.Сазерленд и Д.Коэн предложили следующий алгоритм. Прямые, которым
принадлежат ребра прямоугольника, разбивают плоскость на девять
областей, каждой из которых присваивается четырехразрядный код. Каждый
бит этого кода "отвечает" за одну из прямых: 1-й (старший) бит - за
прямую 
, 2-й - за прямую 
, 3-й - за 
, 4-й - за 
. Если в коде
области какой-либо бит установлен в 1, то это означает, что она
отделена от окна соответствующей прямой. Схема идентификации областей
приведена на рис. 5.1.
Концевым точкам отрезков сцены теперь можно присвоить коды в зависимости от расположения точек. Ясно, что если коды обоих концов отрезка равны нулю, то отрезок полностью лежит внутри окна. Для дальнейшего анализа воспользуемся операцией логического умножения кодов (поразрядное логическое "И"). Тогда таблица истинности для кодов, согласно схеме на рис. 5.1, будет выглядеть следующим образом:
 |
 |
 |
 |
 |
 |
 |
 |
|
|
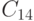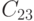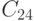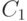T | F | F | F | T | T | F | F |
|
F | T | F | F | F | F | T | T |
|
F | F | T | F | T | F | T | F |
|
F | F | F | T | F | T | F | T |
|
T | F | T | F | T | T | T | F |
|
T | F | F | T | T | T | F | T |
|
F | T | T | F | T | F | T | T |
|
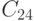F | T | F | T | F | T | T | T |
Из сопоставления таблицы с рисунком видно, что если произведение кодов концов отрезка принимает значение <True>, то отрезок целиком лежит по одну сторону какой-то из прямых, причем внешнюю сторону по отношению к окну, следовательно, он полностью невидим. Во всех остальных случаях отрезок может частично лежать внутри окна, поэтому для определения их видимой части надо решать задачу о пересечении отрезков с ребрами окна. При этом желательно по возможности сократить число перебираемых пар "отрезок-ребро".
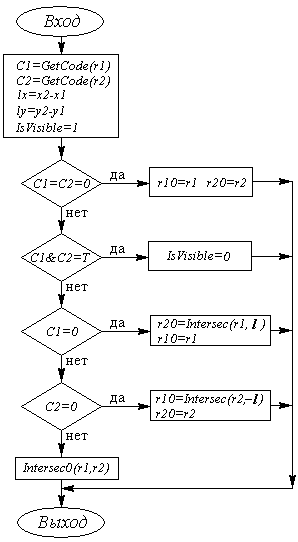
В самом общем случае существуют две точки пересечения отрезка с ребрами, и эти две точки принимаются за новые концевые точки изображаемого отрезка. Но сначала можно выделить некоторые более простые частные случаи, поиск пересечений для которых является более эффективным. Прежде всего это горизонтальные и вертикальные отрезки, для которых поиск точки пересечения тривиален. Далее, если код одного из концов отрезка равен нулю, то существует только одно пересечение этого отрезка с ребром (или с двумя ребрами, если отрезок проходит через угловую точку окна). На рис. 5.2 приведена общая блок-схема алгоритма отсечения для одного произвольно направленного отрезка.
В блок-схеме используются следующие соглашения и обозначения:
- входными данными являются точки
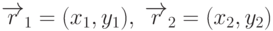, массив координат окна 
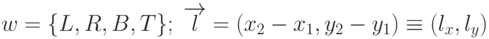; - на выходе получаем новые концевые точки
, а также значение переменной IsVisible (0 - отрезок невидимый); - используются следующие вспомогательные функции:
GetCode(r) - определение кода точки;
Intersec0(r1,l) - поиск пересечения отрезка со сторонами окна при условии, что обе точки лежат вне окна; если пересечения нет, устанавливает переменную IsVisible в 0;
Intersec(r1,l) - поиск пересечения отрезка со сторонами окна при условии, что точка r1 лежит в окне;
C1, C2 - коды точек r1, r2.
Анатолий Федоров
| Россия, Москва, Московский государственный университет им. М. В. Ломоносова, 1989 |