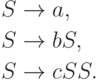| Помогите решить задание лекции 3 курс Математическая теория формальных языков |
Синтаксический разбор
13.2. Восходящий разбор
Определение 13.2.1. Протоколом
правостороннего вывода в контекстно-свободной грамматике 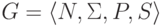 будем называть
обращенную
последовательность правил,
примененных в этом выводе.
Формально говоря,
протоколом правостороннего вывода
будем называть
обращенную
последовательность правил,
примененных в этом выводе.
Формально говоря,
протоколом правостороннего вывода
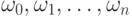
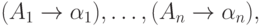
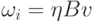 и
и  для некоторых
для некоторых 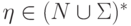 ,
, 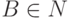 ,
,  ,
, 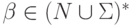 ,
то An-i = B
и
,
то An-i = B
и 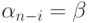 .
.Пример 13.2.2. Рассмотрим контекстно-свободную грамматику
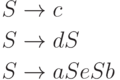
![\xymatrix @=6pt {
& & & & S\ar[ddllll]\ar[ddll]\ar[dd]\ar[ddrr]\ar[ddrrrr] \\
\\
a & & S\ar[dd] & & e & & S\ar[ddl]\ar[ddr] & & b \\
\\
& & c & & & d & & S\ar[dd] \\
\\
& & & & & & & c
}](/sites/default/files/tex_cache/cb4985ced830d8fbadae5d6e430cbbf8.png)


Лемма 13.2.3. Разным правосторонним выводам в одной и той же контекстно-свободной грамматике соответствуют разные протоколы.
Протокол правостороннего вывода в контекстно-свободной грамматике является естественным описанием соответствующего дерева вывода в порядке постфиксного обхода (postorder traversal). (Постфиксный обход упорядоченного дерева можно определить рекурсивно так: сначала выполняется постфиксный обход первого непосредственного потомка корня, затем второго и т. д., а в самом конце посещается корень дерева.)
Например, протокол правостороннего вывода из примера 13.2.2 задает процесс постепенного конструирования дерева вывода, изображенный ниже.
![\newcommand{\rb}[1]{\raisebox{0pt}[8pt]{$ #1 $}}
\entrymodifiers={=<3.3mm>[o]}
\xymatrix @=0mm {
& & & & \boldsymbol{S}\ar[ddddll] \\
\\
\\
\\
\rb{\boldsymbol{a}} & & \rb{c}
\\%}
\\
%&\xymatrix @=0mm {
& & & & \boldsymbol{S}\ar[ddddll] \\
\\
& & & & & & & \boldsymbol{S}\ar[ddr] \\
\\
\rb{\boldsymbol{a}} & & \rb{c} & & \rb{\boldsymbol{e}} & & \rb{\boldsymbol{d}} & & \rb{c}
\\%}
\\
%&\xymatrix @=0mm {
& & & & \boldsymbol{S}\ar[ddddll] & & \boldsymbol{S}\ar[dddd]\ar[ddr] \\
\\
& & & & & & & S\ar[ddr] \\
\\
\rb{\boldsymbol{a}} & & \rb{c} & & \rb{\boldsymbol{e}} & & \rb{d} & & \rb{c}
\\%}
\\
%&\xymatrix @=0mm {
& & & & & \boldsymbol{S}\ar[ddddddlllll]<-1mm>\ar[ddl]\ar[ddddddl]\ar[ddr]\ar[ddddddrrrrr]<1mm> \\
\\
& & & & S\ar[ddddll] & & S\ar[dddd]\ar[ddr] \\
\\
& & & & & & & S\ar[ddr] \\
\\
\rb{a} & & \rb{c} & & \rb{e} & & \rb{d} & & \rb{c} & & \rb{b}
}](/sites/default/files/tex_cache/f4d456a4d68b609074ccdf21dd7117a6.png)
Определение 13.2.5. Правым разбором (right parse) слова w в контекстно-свободной грамматике G называется протокол любого правостороннего вывода слова w в грамматике G.
Пример 13.2.6. Правым разбором слова aceaacecbecbb в грамматике из примера 13.2.2 является последовательность
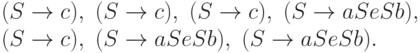
Определение 13.2.7. Процесс нахождения правого разбора слова w в~заданной контекстно-свободной грамматике G называется восходящим разбором (bottom-up parsing).
Определение 13.2.8.
Пусть даны контекстно-свободная грамматика 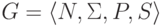 и МП-автомат
и МП-автомат 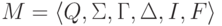 .
Будем говорить, что МП-автомат M - восходящий магазинный анализатор
(bottom-up, left-to-right parser)
для грамматики G,
если
.
Будем говорить, что МП-автомат M - восходящий магазинный анализатор
(bottom-up, left-to-right parser)
для грамматики G,
если  и существует такой
гомоморфизм
и существует такой
гомоморфизм 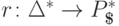 ,
что для каждого
вычислительного процесса
(МП-автомата M ),
допускающего слово
,
что для каждого
вычислительного процесса
(МП-автомата M ),
допускающего слово  ,
образ протокола этого вычислительного процесса при гомоморфизме r
является протоколом некоторого правостороннего вывода
слова w
в грамматике
,
образ протокола этого вычислительного процесса при гомоморфизме r
является протоколом некоторого правостороннего вывода
слова w
в грамматике 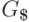 .
.
Пример 13.2.9.
Рассмотрим контекстно-свободную
грамматику 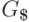 из примера 13.1.17.
Язык
из примера 13.1.17.
Язык 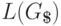 распознается недетерминированным МП-автоматом
распознается недетерминированным МП-автоматом 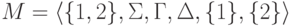 ,
где
,
где
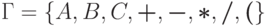
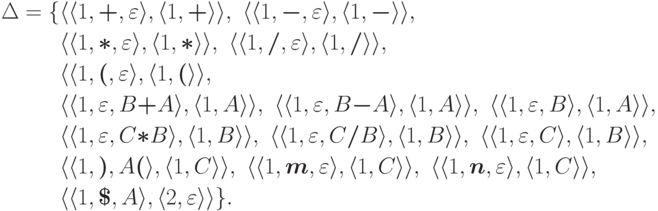
Определение 13.2.10.
Контекстно-свободная грамматика 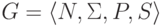 принадлежит классу LR(1),
если для любых
принадлежит классу LR(1),
если для любых 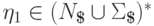 ,
, 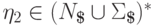 ,
, 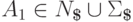 ,
, 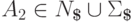 ,
, 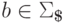 ,
, 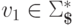 ,
, 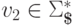 ,
, 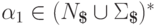 ,
,  из условий
из условий

 .
.Замечание 13.2.11. Классу LR(1) принадлежат те языки, для которых возможен восходящий разбор слова при чтении слева направо с заглядыванием на один символ вперед.
Замечание 13.2.12. Буква L в названии класса LR(1) означает, что входное слово читается слева направо (left-to-right). Буква R означает, что строится правосторонний вывод (rightmost derivation). Число 1 указывает на то, что на каждом шаге для принятия решения используется один символ неразобранной части входного слова.
Теорема 13.2.13. Для каждой грамматики из класса LR(1) существует детерминированный восходящий магазинный анализатор.
Доказательство можно найти в [2, с. 420-447].
Теорема 13.2.14. Грамматики из класса LR(1) порождают только детерминированные контекстно-свободные языки.
Теорема 13.2.15. Каждая грамматика из класса LL(1) принадлежит также классу LR(1).
Упражнение 13.2.16. Найти все правые разборы слова bbacba в грамматике
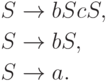
Упражнение 13.2.17. Найти детерминированный восходящий магазинный анализатор для грамматики

Упражнение 13.2.18. Найти детерминированный восходящий магазинный анализатор для грамматики