| Помогите решить задание лекции 3 курс Математическая теория формальных языков |
Синтаксический разбор
Определение 13.1.14. Протоколом
вычислительного процесса
МП-Автомата 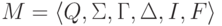 будем называть последовательность переходов,
примененных в этом вычислительном процессе.
Формально говоря,
протоколом вычислительного процесса
будем называть последовательность переходов,
примененных в этом вычислительном процессе.
Формально говоря,
протоколом вычислительного процесса
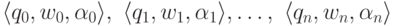
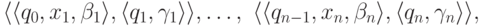
 ,
а через
,
а через 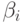 и
и 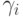 обозначены кратчайшие слова из
обозначены кратчайшие слова из  ,
удовлетворяющие условиям
,
удовлетворяющие условиям
 .
.Пример 13.1.15. Протоколом вычислительного процесса из примера 13.1.10 является последовательность
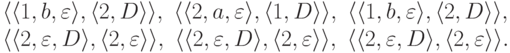
Определение 13.1.16.
Для каждой контекстно-свободной грамматики 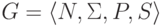 обозначим через
обозначим через 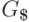 контекстно-свободную грамматику
контекстно-свободную грамматику 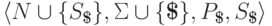 ,
где
,
где  и
и 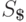 -
два различных новых символа, не принадлежащие множеству
-
два различных новых символа, не принадлежащие множеству  ,
и
,
и 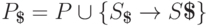 .
Грамматику
.
Грамматику 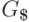 будем называть грамматикой с маркером конца строки.
Терминальный алфавит
грамматики
будем называть грамматикой с маркером конца строки.
Терминальный алфавит
грамматики 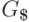 (то есть множество
(то есть множество  )
будем обозначать через
)
будем обозначать через 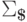 .
Нетерминальный алфавит
.
Нетерминальный алфавит 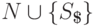 будем обозначать через
будем обозначать через 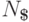 .
.
Пример 13.1.17.
Рассмотрим контекстно-свободную грамматику G
с терминальным алфавитом  ,
вспомогательным алфавитом N = {S,A,B,C}
и
правилами
,
вспомогательным алфавитом N = {S,A,B,C}
и
правилами
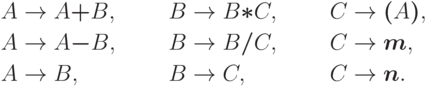
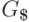 с маркером конца строки:
с маркером конца строки: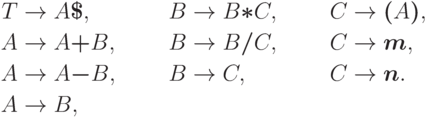
Замечание 13.1.18.
Очевидно, что 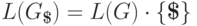 .
.
Лемма 13.1.19. Если ![\smash[b]{
S_\eos \overstar{\myunderset{ G_\eos }{\Rightarrow }} \eta \eos \theta }](/sites/default/files/tex_cache/883083eb587243f096d012c1afbd2ee9.png) , где
, где 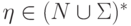 и
и 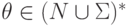 , то
, то 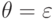 .
.
Доказательство.
Очевидно, что если ![\smash[b]{
S \eos \overstar{\myunderset{ G_\eos }{\Rightarrow }} \omega }](/sites/default/files/tex_cache/620391cba6253f92e3b2507732e02754.png) ,
то
слово
,
то
слово 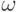 не содержит символа
не содержит символа 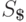 .
.
Теперь докажем индукцией по длине вывода,
что если 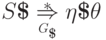 ,
то
,
то 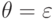 .
Пусть на последнем шаге в этом выводе применялось правило
.
Пусть на последнем шаге в этом выводе применялось правило 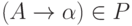 .
.
Если 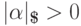 ,
то
,
то  ,
что невозможно (очевидно, что если
,
что невозможно (очевидно, что если 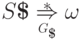 ,
то слово
,
то слово 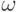 не содержит символа
не содержит символа 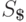 ).
).
Если 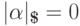 ,
то рассмотрим два случая.
При
,
то рассмотрим два случая.
При
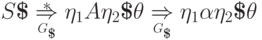
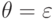 обеспечивается предположением индукцией.
Случай
обеспечивается предположением индукцией.
Случай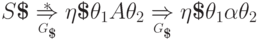
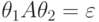 .
.Определение 13.1.20.
Пусть даны контекстно-свободная грамматика 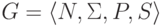 и МП-автомат
и МП-автомат 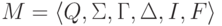 .
Будем говорить, что МП-автомат M - нисходящий магазинный анализатор
(или предсказывающий анализатор,
top-down, left-to-right parser, predictive parser)
для грамматики G,
если
.
Будем говорить, что МП-автомат M - нисходящий магазинный анализатор
(или предсказывающий анализатор,
top-down, left-to-right parser, predictive parser)
для грамматики G,
если  и существует такой
гомоморфизм
и существует такой
гомоморфизм 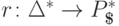 ,
что
для каждого
вычислительного процесса
(МП-автомата M ),
допускающего слово
,
что
для каждого
вычислительного процесса
(МП-автомата M ),
допускающего слово  ,
образ протокола этого вычислительного процесса при гомоморфизме
,
образ протокола этого вычислительного процесса при гомоморфизме 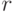 является протоколом некоторого левостороннего вывода
слова w
в грамматике
является протоколом некоторого левостороннего вывода
слова w
в грамматике 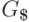 .
(При задании гомоморфизма r
конечные множества
.
(При задании гомоморфизма r
конечные множества  и
и  рассматриваются как два алфавита.)
рассматриваются как два алфавита.)
Пример 13.1.21.
Рассмотрим контекстно-свободную
грамматику 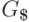 из примера 13.1.17.
Язык
из примера 13.1.17.
Язык 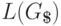 распознается недетерминированным МП-автоматом
распознается недетерминированным МП-автоматом 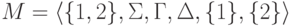 ,
где
,
где