КубГТУ: 23-К-АС2:

Табличный процессор Excel в экономических и финансовых расчетах
[+]
Опубликован: 26.05.2021 | Уровень: для всех | Доступ: платный
Лекция 4:

Построение графиков функций и использование логических формул
A
|
версия для печати
< Лекция 3 || Лекция 4 || Лекция 5 >
Аннотация: Цель работы: научиться определять значения функций и строить графики, а также использовать логические функции в табличном процессоре Excel. Содержание работы: Построение графика функции с одной переменной. Построение графика функции с двумя условиями. Построение графика функции с тремя условиями. Построение двух графиков в одной системе координат. Построение поверхности. Порядок выполнения работы: Изучить методические указания. Выполнить задания. Оформить отчет и ответить на контрольные вопросы.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Построение графика функции

Процесс построения графика функции состоит из двух этапов:

  • создание таблицы значений функции
  • непосредственного построения ее графика.

Для построения графика функции необходимо первоначально построить таблицу ее значений при различных значениях аргумента, причем аргумент изменяют обычно с фиксированным шагом. Шаг выбирают небольшим, так чтобы таблица значений функции отражала ее поведение на интервале табуляции.

Рассмотрим технологию построения графика на примере функции $y=cos^{2}(\pi x)$ при $x\in [0; 1]$ .

Создание таблицы значений функции

В нашем случае возьмем в качестве шага изменения аргумента, например, 0.1. Нам надо найти у(0), у(0.1), у(0.2), ..., у(1). С этой целью в ячейки диапазона A1:А11 последовательно введем 0, 0.1, ..., 1, т. е. значения переменной х. Отметим, что эта последовательность значений представляет собой арифметическую прогрессию.

Ввести в ячейки диапазона ряд последовательных значений, образующих арифметическую прогрессию, можно двумя способами.

Первый способ заключается в следующем:

  1. В ячейки А1 и А2 введите первый и второй члены арифметической прогрессии, т.е. 0 и 0,1
  2. Выделите диапазон ячеек А1:А2.
  3. Расположите указатель мыши на маркере заполнения выделенного диапазона (рис. 4.1 рис. 4.1) и протяните его вниз (в данном случае на диапазон A3:А11) до тех пор, пока не получится числовой ряд нужной длины (рис. 4.2 рис. 4.2).

Второй способ позволяет пользоваться диалоговым окном Прогрессия. Для этого:

  1. В ячейку А1 введите первый член арифметической профессии.
  2. Выберите команду Главная > Редактирование > Заполнить > Прогрессия.
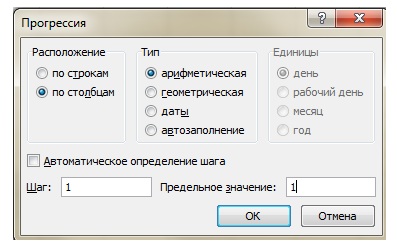
  3. В появившемся диалоговом окне Прогрессия (рис. 4.3 рис. 4.3) в группе Расположение выбираем переключатель по столбцам, а в группе Тип – переключатель арифметическая. В поле Шаг введите значение 0,1, а в поле Предельное значение – 1.
  4. Нажмите кнопку ОК.
Вид указателя мыши на маркере заполнения

Рис. 4.1. Вид указателя мыши на маркере заполнения
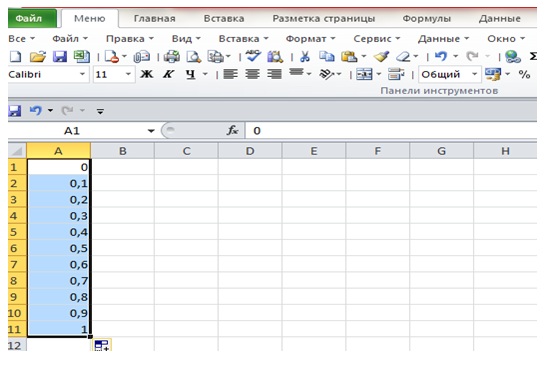
Арифметическая последовательность, построенная по первым ее двум членам с помощью маркера заполнения

Рис. 4.2. Арифметическая последовательность, построенная по первым ее двум членам с помощью маркера заполнения
Диалоговое окно Прогрессия

Рис. 4.3. Диалоговое окно Прогрессия

Диалоговое окно Прогрессия закроется, а на рабочем листе автоматически будет построена требуемая прогрессия.

Примечание. Диалоговое окно Прогрессия, отображаемое на экране выбором команды Главная > Редактировать > Заполнить > Прогрессия, также позволяет создавать геометрические прогрессии.

В ячейку В1 введите формулу: =СОS(ПИ( )*А1)^2.

Ввод формул в ячейку можно производить либо с клавиатуры, либо с помощью диалогового окна Мастер функций, которое отображается на экране либо выбором команды Формулы > Вставить Функцию, либо нажатием кнопки Вставка функции панели инструментов Стандартная. Мастер функций содержит список всех функций рабочего листа, справки по их синтаксису и примеры применения.

Продемонстрируем работу с мастером функций на примере ввода упомянутой выше формулы.

  1. Выберите ячейку В1.
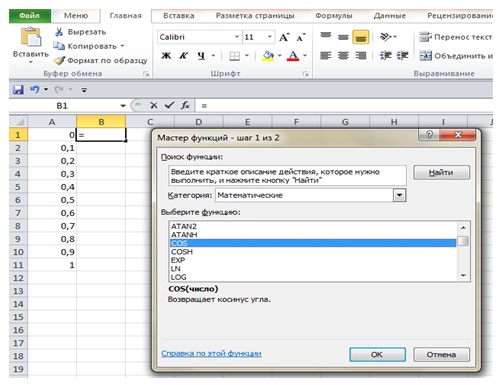
  2. Нажмите кнопку Вставка функции панели инструментов Стандартная, либо выберите команду Формулы > Вставить Функцию. На экране отобразится диалоговое окно Мастер функций – шаг 1 из 2 (рис. 4.4 рис. 4.4). Оно состоит из двух частей:
  3. Категория – со списком двенадцати категорий функций;
  4. Функция – со списком имен функций, входящих в выбранную категорию.

Категория Полный алфавитный перечень содержит все встроенные функции и их имена упорядочены в алфавитном порядке, категория 10 недавно использовавшихся содержит имена десяти последних примененных функций. Эта категория ускоряет вызов функций, постоянно используемых пользователем.

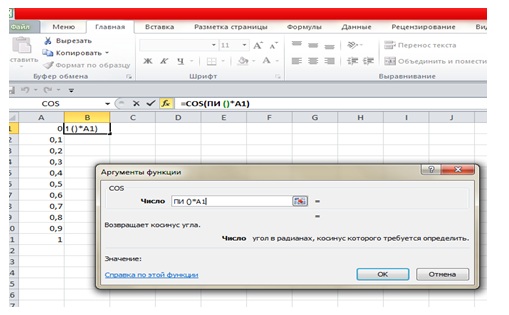
  1. Функция cos относится к категории Математические. Выберите эту функцию и нажмите кнопку ОК. На экране отобразится панель формул (рис. 4.5 рис. 4.5).
Диалоговое окно Мастер функций – шаг 1 из 2

Рис. 4.4. Диалоговое окно Мастер функций – шаг 1 из 2
Панель формул

Рис. 4.5. Панель формул

В поле Число вводится аргумент функции – в рассматриваемом примере это ПИ ()*А1. С помощью клавиатуры в это поле введите только ПИ ( )*, а ссылку на ячейку А1 в формулу добавьте, щелкнув по ячейке А1 на рабочем листе. Конечно, ее можно было также ввести с клавиатуры, но предложенный способ дает дополнительную проверку правильности ввода. После нажатия кнопки ОК в ячейку В1 будет введена формула:

=COS(ПИ()*Al)

Примечание. При использовании мастера функции перед вводом формулы в ячейку не надо вводить знак =, он вставляется в формулу автоматически.

  1. С помощью клавиатуры добавьте в формуле =COS(ПИ ())*А1 операцию возведения в квадрат функции cos. После всех описанных действий в ячейке В1 должна появиться формула =COS(ПИ()*Al)^2

Таким образом, пока найдено значение функции cos2(x) для значения х из ячейки A1. Теперь нам осталось найти значения этой функции для диапазона ячеек А2:А11.

Для этого:

  1. Выберите ячейку В1.
  2. Расположите указатель мыши на маркере заполнения выделенной ячейки и протяните его вниз на диапазон В2:В11.

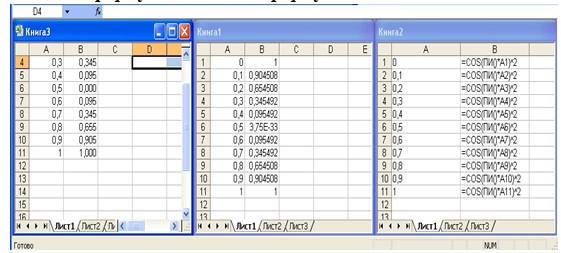
Процесс создания таблицы значений функции завершен (рис. 4.6 рис. 4.6).

На рис. 4.6 рис. 4.6 на правом рабочем листе приведены формулы, введенные в ячейки рабочего листа. Для того чтобы в ячейках рабочего листа отображались не значения, а формулы, надо выбрать команду Формулы > Зависимости формул и Показать формулы.

Результат табуляции функции до и после форматирования данных

Рис. 4.6. Результат табуляции функции до и после форматирования данных

На среднем рабочем листе (рис. 4.6 рис. 4.6) приведен результат табуляции функции. Выглядит он не очень презентабельно: после десятичной точки отображается различное количество десятичных знаков. Кроме того, происходит перемешивание числового и экспоненциального форматов.

А именно, в ячейке В6 вместо 0 отображается 3.75Е-33, что приблизительно и равно нулю. Поэтому форматы надо привести к какому-то общему виду, например, как показано на левом рабочем листе: значения аргумента выводятся в числовом формате с точностью до одного знака после десятичной точки, а значения функции – с точностью до трех знаков после десятичной точки. Отформатируем, например, значения аргумента.

Для этого надо выбрать диапазон A1:A11. Это можно сделать, например, следующим способом. Выберите ячейку А1, а затем при нажатой клавише <Shift> выделите ячейку А11. Диапазон А1:А11 выбран.

Переходим к форматированию данных. Выберите команду Главная > Число. В появившемся диалоговом окне Формат ячеек: Число в списке Числовые форматы выберите Числовой, а в поле Число десятичных знаков введите 1. Нажмите кнопку ОК. Данные в Al:A11 будут отформатированы, как показано на левом рабочем листе (рис. 4.6 рис. 4.6). Аналогичным образом разберитесь с диапазоном В1:В11.

Построение графика

Перейдем теперь к конструированию графика cos2(xх) функции по существующей таблице значений аргументов и соответствующих значений функции. Для этого:

  1. Выберите команду Вставка > Диаграмма.
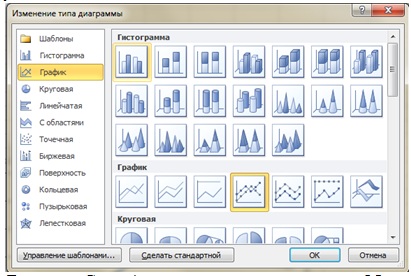
  2. В появившемся диалоговом окне Мастер диаграмм на выберите вариант График, а в списке Вид укажите стандартный график (рис. 4.7 рис. 4.7). Нажмите кнопку Далее.
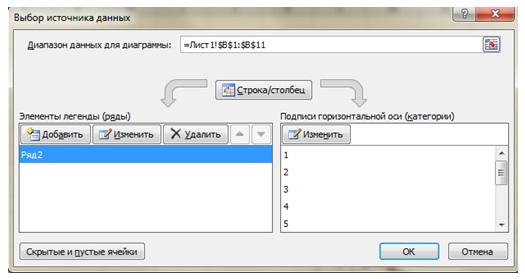
  3. Чтобы изменить (шаг 2 из 4): источник данных диаграммы (которое позднее переименовывается в окно Исходные данные) необходимо нажать на график, затем выбрать вкладку Конструктор, затем вкладку Данные, Выбрать данные. В поле Диапазон автоматически будет введена ссылка на необходимый диапазон в абсолютном формате. Проверьте его, удалите 1 ряд. В итоге у вас должно получится, что Диапазон, =Лист1!$В1$:$В$11.

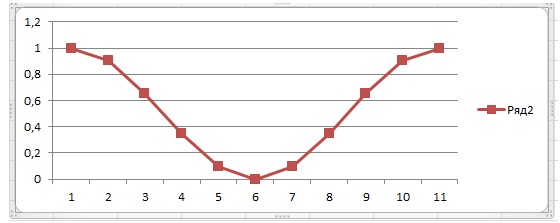
Обратите внимание на полученный график функции, отображаемый на вкладке Диапазон данных. В нем по оси ординат откладываются значения функции, а вот по оси абсцисс порядковые номера точек, а не значения аргумента.

Для того чтобы по оси абсцисс откладывались значения аргумента, надо выделить диаграмму и воспользоваться командой Конструктор > Данные > Выбрать данные, далее Подписи горизонтальной оси (категории) > Изменить и указать диапазон ячеек в которых расположен аргумент х функции.

Вкладка Стандартные диалогового окна Мастер диаграмм (шаг 1 из 4): тип диаграммы

Рис. 4.7. Вкладка Стандартные диалогового окна Мастер диаграмм (шаг 1 из 4): тип диаграммы
Вкладка Диапазон данных диалогового окна Исходные данные

Рис. 4.8. Вкладка Диапазон данных диалогового окна Исходные данные

Создав диаграмму, можно изменить любой из ее элементов. Например, можно изменить вид осей, добавить название диаграммы, переместить или скрыть легенду, а также добавить дополнительные элементы.

Чтобы изменить диаграмму, выполните одно или несколько из указанных ниже действий.

  • Изменение вида осей диаграммы. Можно указать масштаб осей и изменить промежутки между значениями или категориями. Для удобства чтения диаграммы можно добавить на оси деления указать величину промежутков между ними.
  • Добавление к диаграмме названий и меток данных. Для пояснения отображенных на диаграмме данных можно добавить название диаграммы, названия осей и метки данных.
  • Добавление легенды и таблицы данных Можно отобразить или скрыть легенду, изменить ее расположение или элементы. Для некоторых диаграмм также можно отобразить таблицу данных, в которой содержатся ключи легенды и значения, представленные на диаграмме.
  • Применение специальных параметров для диаграмм разных типов Для различных типов диаграмм можно применять различные специальные линии (например, коридор колебания и линии тренда), полосы (например, полосы повышения и понижения и планки погрешностей), маркеры данных и т.д.

Вместо того чтобы добавлять или изменять элементы диаграммы и форматировать их вручную, можно быстро применить к данным готовый макет или стиль диаграммы. В приложении Excel существует множество полезных готовых макетов и стилей, которые можно адаптировать, изменив вручную макет или формат отдельных элементов диаграммы, таких как область диаграммы, область построения, ряды данных и легенда.

При использовании готового макета диаграммы на ней в определенном порядке отображается заданный набор элементов (например, названия, легенда, таблица данных или метки данных). Можно подобрать подходящий макет из предоставленных для диаграмм конкретного типа.

При использовании готового стиля диаграммы ее форматирование основано на примененной теме документа, поэтому внешний вид диаграммы будет соответствовать цветам темы (набору цветов), шрифтам темы (набору шрифтов заголовков и основного текста) и эффектам темы (набору границ и заливок), принятым в организации или заданным пользователем.

Собственные стили или макеты диаграмм создавать нельзя, но можно создать шаблоны диаграмм, содержащие нужный макет и форматирование.

Помимо применения готового стиля диаграммы можно легко изменить форматирование ее отдельных элементов, например маркеров данных, области диаграммы, области построения, чисел и текста в названиях и подписях, что привлечет внимание и сделает диаграмму оригинальной. Можно также применять стили фигур и стили WordArt или форматировать фигуры и текст в элементах диаграммы вручную.

Чтобы изменить форматирование диаграммы, выполните одно или несколько из указанных ниже действий:

  • Заливка элементов диаграммы. Для привлечения внимания к определенным элементам диаграммы можно залить их цветом, текстурой, рисунком или применить градиентную заливку.
  • Изменение контуров элементов диаграммы. Для выделения элементов диаграммы можно изменить цвет, стиль или толщину линий.
  • Добавление специальных эффектов к элементам диаграммы. Для придания диаграмме завершенности к ее элементам можно применить специальные эффекты, например тень, отражение, свечение, сглаживание краев, рельеф или объемное вращение.
  • Форматирование текста и чисел Текст и числа в названиях, подписях и надписях на диаграмме можно форматировать так же, как текст и числа на листе. Чтобы выделить текст или число, можно даже применять стили WordArt.
Вкладка Конструктор: параметры диаграммы

Рис. 4.9. Вкладка Конструктор: параметры диаграммы
Диалоговое окно Макет: параметры диаграммы

Рис. 4.10. Диалоговое окно Макет: параметры диаграммы
Результат построения графика функции

Рис. 4.11. Результат построения графика функции

Математические функции рабочего листа

Наиболее часто употребляемые стандартные математические функции рабочего листа приведены в табл. 4.1 таблица 4.1.

Таблица 4.1. Математические функции
Функция (рус.) Функция (англ.) Описание
1 2 3
ABS (число) ABS (number) Возвращает абсолютную величину аргумента
ACOS (число) ACOS (number) Возвращает арккосинус аргумента
ASIN (число) ASIN (number) Возвращает арксинус аргумента
ATAN (число) ATAN (number) Возвращает арктангенс аргумента
COS (число) COS (number) Возвращает косинус аргумента
EXP (число) EXP (number) Возвращает экспоненту аргумента, т.е результат возведения основания натурального логарифма в степень, равную значению аргумента
LN (число) LN (number) Возвращает натуральный логарифм аргумента
LOG (число) LOG (number) Возвращает логарифм аргумента по данному основанию, если основание опущено, то оно полагается равным 10
LOG10 (число; основание) LOG10 (number; base) Возвращает десятичный логарифм аргумента
SIN (число) SIN (number) Возвращает синус аргумента
TAN (число) TAN (number) Возвращает тангенс аргумента
ЗНАК (число) SGN (number) Возвращает знак аргумента
ОСТАТ (число; делитель) MOD (number1; number1) Возвращает остаток от деления числа на делитель
ПИ ( ) PI ( ) Возвращает значение числа ? с точностью до 15 знаков (в данном случае 3.14159265358979). обратите внимание на то, что функция ПИ ( ) не имеет аргумента
СЛЧИС ( ) RND ( ) Возвращает случайное число между 0 и 1. Чтобы получить случайное вещественное число между a и b, можно использовать следующую формулу: СЛЧИС ( )*(b-a)+a
ЦЕЛОЕ (число) INT (number) Округляет число до ближайшего меньшего целого

График функции с двумя условиями

Рассмотрим пример построения графика функции при $х\in[0;1]$$:

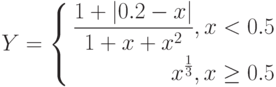
$$ Y=\left\{ \begin{aligned} \frac{1+|0.2-x|}{1+x+x^{2}},x<0.5 \\ x^{\frac{1}{3}}, x\geq0.5 \end{aligned} \right. $$

График строится по принципам, представленным в п. 4.1 "Построение графика функции" "Построение графиков функций и использование логических формул" , за исключением того, что в ячейку В1 вводится формула:

=ЕСЛИ(А1<0.5;(1+ABS(0.2-А1))/(1+А1+А1^2);А1^ (1/3))

Примечание. Обратите внимание на то, что для возведения в степень в коде используется соответствующая операция, т.е. А1^(1/3), а не функция рабочего листа степень, т. е. степень (А1; 1/3). В обоих случаях получается один и тот же результат, но, применение операции возведения в степень здесь более разумно, т. к. делает код более очевидным.

В коде фигурирует функция логического ветвления Если (IF), которая имеет следующий синтаксис:

ЕСЛИ (лог выражение; значение_если_истина; значение_если_ложь)

Рассмотрим ее аргументы:

  • лог выражение – это любое значение или выражение, принимающее значения истина или ложь. Например, А10=100 – это логическое выражение; если значение в ячейке А10 равно 100, то выражение принимает значение ИСТИНА. В противном случае – ЛОЖЬ. Данный аргумент может быть использован в любом операторе сравнения.
  • значение_если_истина – это значение, которое возвращается, если лог выражение равно ИСТИНА. Например, если этот аргумент – строка "План реализации выполнен" и лог выражение равно ИСТИНА, тогда функция ЕСЛИ отобразит текст План реализации выполнен. Если лог выражение равно, ИСТИНА, а значение_если_истина пусто, то возвращается значение 0. Чтобы отобразить слово ИСТИНА, необходимо использовать логическое значение ИСТИНА для этого аргумента. значение_если_истина может быть формулой.
  • значение_если_ложь – это значение, которое возвращается, если лог выражение равно ЛОЖЬ. Например, если этот аргумент – строка "План реализации перевыполнен" и лог выражение равно ЛОЖЬ, то функция ЕСЛИ отобразит текст План реализации перевыполнен. Если лог выражение равно ЛОЖЬ, а значение_если_ложь опущено (т. е. после значение_если_истина нет точки с запятой), то возвращается логическое значение ЛОЖЬ. Если лог выражение равно ЛОЖЬ, а значение_если_ложь пусто (т. е. после значение_если_истина стоит точка с запятой с последующей закрывающей скобкой), то возвращается значение 0. значение_если_ложь может быть формулой.

Логические функции

В MS Excel имеются функции логических условий, перечисленные в табл. 4.2. таблица 4.2

Таблица 4.2. Функции логических условий
Функция (рус.) Функция (англ.) Описание
1 2 3
И (лог знач1; лог знач2; …) AND (arg1, arg2, …) Логическое умножение.
Возвращает значение ИСТИНА, если все аргументы имеют значение ИСТИНА; возвращает значение ЛОЖЬ, если хотя бы один аргумент имеет значение ЛОЖЬ.
Например, И (2+2=4; 2+3=5) возвращает значение ИСТИНА.
Если ячейка В4содержит число из интервала от 1 до 100, то функция И (1<В4; В4<100) возвращает значение ИСТИНА, а в противном случае – ЛОЖЬ.
ИЛИ (лог знач1; лог знач2; …) OR (arg1, arg2, …) Логическое сложение.
Возвращает ИСТИНА, если хотя бы один из аргументов имеет значение ИСТИНА; возвращает ЛОЖЬ, если все аргументы имеют значение ЛОЖЬ.
Например, И (2+2=4; 2+3=6) возвращает значение ИСТИНА.
Если ячейка В4 содержит число меньше 1 или больше 100, то ИЛИ (В4<1; В4>100) возвращает значение ИСТИНА, а в противном случае – ЛОЖЬ.
НЕ (лог знач) NOT (arg) Логическое отрицание. Изменяет на противоположное значение логическое значение своего аргумента. Например, НЕ (2+5=5) возвращает значение ИСТИНА.
Если ячейка В4 содержит число меньше 1 или больше 100, то НЕ (ИЛИ(В4<1;В4>100)) возвращает ЛОЖЬ, а в противном случае – ЛОЖЬ.

Примечание. Кроме функции ЕСЛИ в MS Excel имеются еще две функции, использующие логические условия. Это функции:

СЧЁТЕСЛИ (COUNTIF) – подсчитывает количество ячеек внутри диапазона, удовлетворяющих заданному критерию;

СУММЕСЛИ (SUMIF) – суммирует значения тех ячеек диапазона, удовлетворяющих заданному критерию.

График функции с тремя условиями

Рассмотрим пример построения графика функции у при $x\in [0; 1]$ :

$$ Y=\left\{ \begin{aligned} % \nonumber to remove numbering (before each equation) 1+ln(1+x), x<0.2\\ \frac{1+x^{\frac{1}{2}}}{1+x}, x\in[0.2;0.8]\\ 2e^{-2x}, x>0.8 \end{aligned} \right. $$

График строится так, как описано в разд. "Построение графика функции" ранее в этой работе, за исключением того, что в ячейку В1 вводится формула:

=ЕСЛИ(А1<0.2;1+ LN(1+A1); ЕСЛИ(И(А1>=0.2;А1<=0.8);
	(1+А1^(1/2))/(1+А1);2*ЕХР(-2*А1)))

Тот же самый результат можно получить, введя в ячейку В1 более простую формулу:

=ЕСЛИ (A1<0.2; 1+LN (1+A1); ЕСЛИ (А1<=0.8; (1+А1^(1/2))/(1+А1);
	2*ЕХР(-2*А1)))

Два графика в одной системе координат

Рассмотрим пример построения в одной системе координат при $х\in [-3; 0]$ графиков следующих двух функций:

  • y = 2sin(x)
  • z = 3 cos(2x) – sin(x)

Итак, начнем процесс построений.

  1. В ячейки А1, В1 и С1 введите соответственно х, у и z.
  2. Выделите диапазон А1:С1. Выберите команду Главная. На вкладке

Выравнивание появившегося диалогового окна Формат ячеек в группе Выравнивание в списке по горизонтали укажите значение по правому краю. Нажмите кнопку ОК. Заголовки столбцов окажутся выровненными по правому краю.

  1. В диапазон ячеек А2:А17 введите значения аргумента х от -3 до 0 с шагом 0.2.
  2. В ячейки В2 и С2 введите формулы: =2*SIN(A2), =3*COS(2*A2)-SIN(A2)
  3. Выделите диапазон В2:С2, расположите указатель мыши на маркере заполнения этого диапазона и пробуксируйте его вниз так, чтобы заполнить диапазон В3:С17.
  4. Выделите диапазон В3:С17. Выберите команду Вставка > Диаграмма.
  5. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы выберите значение График. Нажмите кнопку Далее.
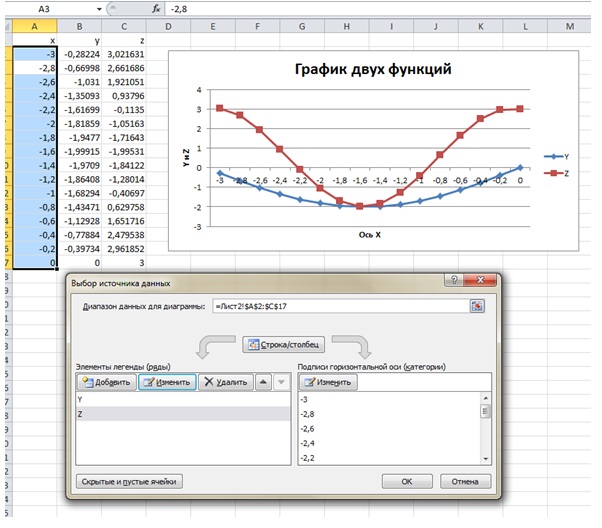
  6. На вкладке Данные > выбрать данные диалогового окна Исходные данные в поле ввода Подписи оси X укажите ссылку на диапазон А2:А17, значения из которого откладываются по оси абсцисс (рис. 4.12 рис. 4.12). В списке Ряд приводятся ряды данных, откладываемых по оси ординат (в нашем случае имеется два ряда данных). Эти ряды автоматически определяются на основе ссылки, указанной в поле ввода Диапазон предыдущего шага алгоритма. В поле Значения автоматически выводится ссылка на диапазон, соответствующий выбранному ряду из списка Ряд. В поле ввода Имя отображается ссылка на ячейку, в которой содержится заголовок соответствующего ряда. Этот заголовок в дальнейшем используется мастером диаграмм для создания легенды.
Вкладка Ряд диалогового окна Исходные данные до задания имен рядов

Рис. 4.12. Вкладка Ряд диалогового окна Исходные данные до задания имен рядов
  1. Выберите в списке Ряд элемент Ряд1. В поле ввода Имя укажите ссылку на ячейку В1, значение из которой будет использоваться в качестве идентификатора данного ряда. Вводить эту ссылку надо не с клавиатуры, а выбором с рабочего листа ячейки В1. Это приведет к тому, что в поле Имя автоматически будет введена ссылка на ячейку в абсолютном формате. В данном случае, =Лист1!$В$1. Теперь осталось только щелкнуть на элементе Ряд1 списка Ряд. Это приведет к тому, что элемент Ряд1 поменяется на у, т. е. на то значение, которое содержится в ячейке В1. Аналогично поступите с элементом Ряд2 списка Ряд. Сначала выберите его, затем в поле ввода Имя укажите ссылку на ячейку С1, а потом щелкните на элементе Ряд2. На рис. 4.13 рис. 4.13 показана вкладка Ряд диалогового окна Исходные данные после задания имен рядов. Теперь можно нажать кнопку Далее.
  2. В появившемся диалоговом окне Мастер диаграмм (шаг 3 из 4): параметры диаграммы на вкладке Заголовки в поле Название диаграммы введите График двух функций, в поле Ось X(категорий) введите х, в поле Ось Y(значений) введите у и z. На вкладке Легенда установите флажок Добавить легенду. Нажмите кнопку Далее.
  3. Нажмите кнопку Готово.

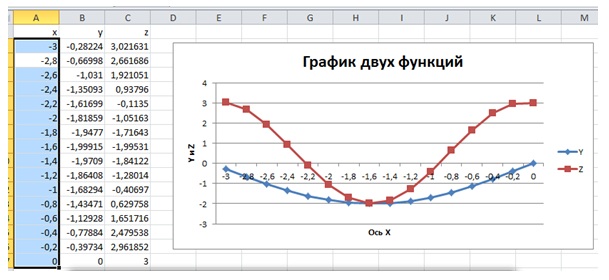
Результат проделанных шагов представлен на рисунке 4.14 рис. 4.14.

Вкладка Ряд диалогового окна Исходные данные после задания имен рядов

Рис. 4.13. Вкладка Ряд диалогового окна Исходные данные после задания имен рядов

Для большей презентабельности построенной диаграммы в ней были произведены следующие изменения по сравнению с оригиналом:

  • Изменена ориентация подписи оси ординат с вертикальной на горизонтальную. Для этого выберите подпись оси ординат. Нажмите правую кнопку мыши и в появившемся контекстном меню укажите команду Формат названия оси. На вкладке Выравнивание диалогового окна Формат названия оси в группе Ориентация установите горизонтальную ориентацию. Нажмите кнопку ОК.
  • Для того чтобы пользователю было легче отличить, какая линия является графиком функции у, а какая – z, изменен вид графика функции z. С этой целью выделите график функции z. Нажмите правую кнопку мыши и в появившемся контекстном меню выберите команду Формат рядов данных. На вкладке Вид диалогового окна Формат ряда данных, используя элементы управления групп Маркер и Линия, установите необходимый вид линии графика. Нажмите кнопку ОК.
  • Изменен фон графика. С этой целью выделите диаграмму (но не область построения). Нажмите правую кнопку мыши и в появившемся контекстном меню выберите команду Формат области диаграммы. На вкладке Вид диалогового окна Формат области диаграммы установите флажок скругленные углы, а используя элементы управления группы Заливка, установите цвет и вид заливки фона. Нажмите кнопку ОК.
Графики функций у(х) и z(x), построенные в одной системе координат

Рис. 4.14. Графики функций у(х) и z(x), построенные в одной системе координат

Построение поверхности

Продемонстрируем технологию построения поверхностей на примере следующей функции, зависящей от двух аргументов:

$z = x^{2}-y^{2}$ при $$х\in [-2; 2], у\in [-1; 1]$ .

Прежде чем воспользоваться мастером диаграмм, надо построить таблицу значений функции z по обоим ее аргументам, например, по аргументу х от -2 до 2 с шагом 0.2, а по у от -1 до 1 с шагом 0.2.

Для этого:

  1. Введите в ячейку А2 значение -2, а в ячейку А3 значение -1.8. Выберите диапазон ячеек А2:А3. Расположите указатель мыши на маркере заполнения этого диапазона и протяните его на диапазон А4:А22. Таким, образом, значения аргумента х протабулированы от -2 до 2 с шагом 0.2.
  2. Введите в ячейку В1 значение -1, а в ячейку С1 значение -0.8. Выберите диапазон ячеек В1:С1. Расположите указатель мыши на маркере заполнения этого диапазона и протяните его на диапазон D1:L1. Значения аргумента у протабулированы от -1 до 1 с шагом 0.2.
  3. В ячейку В2 введите формулу: =$А2^2 – В$1^2.
  4. Выберите ячейку В2, расположите указатель мыши на маркере ее заполнения и протяните его вниз на диапазон В2:L22.

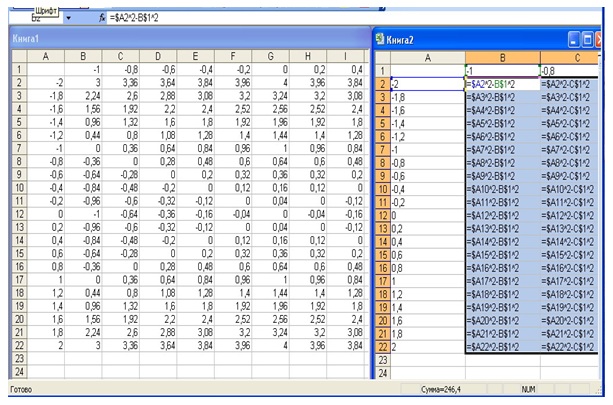
На левом рабочем листе (рис. 4.15 рис. 4.15) показан результат табуляции функции, зависящей от двух аргументов, а на правом – часть формул, которые были введены в ячейке при копировании формулы, введенной в ячейку В2, перемещением маркера заполнения на диапазон В2:L22.

Таблица значений функции, зависящей от двух аргументов

Рис. 4.15. Таблица значений функции, зависящей от двух аргументов

Примечание. Использование в формуле абсолютной ссылки на строку и столбец существенно. Напомним, что знак $ в имени ячейки, стоящий перед номером строки, создает абсолютную ссылку на строку, а перед именем столбца – абсолютную ссылку на столбец. Поэтому при буксировке формулы из ячейки В2 на диапазоны B2:L22, в ячейках этого диапазона будут найдены значения функции z при соответствующих значениях аргументов х и у.

Перейдем к конструированию поверхности по результатам табуляции. Для этого:

  1. Выберите команду Вставка > Диаграмма.
  2. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы на вкладке Стандартные в списке Тип выберите значение Поверхность, а в списке Вид укажите стандартную поверхность. Нажмите кнопку Далее.
  3. В следующем диалоговом окне мастера диаграмм на вкладке Диапазон данных выберите переключатель Ряды в столбцах, т. к. данные располагаются в столбцах. В поле ввода Диапазон приведите ссылку на диапазон данных A1:L22, т. е. диапазон, который содержит в себе как значения аргументов, так и значения функции. Нажмите кнопку Далее.
  4. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): в параметры диаграммы на вкладке Заголовки в поле Название диаграммы введите поверхность, в поле Ось X (категорий) укажите х, в поле Ось Y (рядов данных) задайте у, в поле Ось Z (значений) введите z. На вкладке Легенда сбросьте флажок Добавить легенду. Нажмите кнопку Готово.
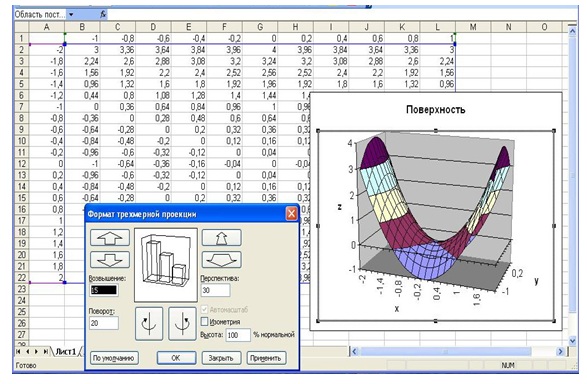
  5. Поверхность построена, как показано на рисунке 4.16 рис. 4.16.
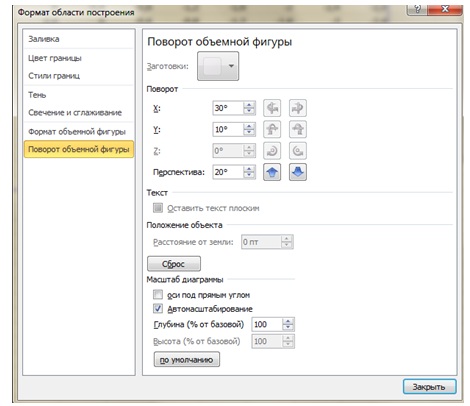
Построенная поверхность и диалоговое окно Формат трехмерной проекции

Рис. 4.16. Построенная поверхность и диалоговое окно Формат трехмерной проекции

Примечание. MS Excel разрешает пользователю не только изменять размеры рабочей области диаграммы посредством маркеров изменения размеров, но и ориентацию поверхности в пространстве. Для этого достаточно выделить диаграмму, а затем выбрать команду Диаграмма > Объемный вид. На экране отобразится диалоговое окно Формат трехмерной проекции, элементы которого как раз и позволяют изменять ориентацию поверхности в пространстве.

ЗАДАНИЯ

Вариант 1.

1. Построить в разных системах координат при $х\in [-2; 2]$ графики функций:

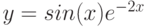
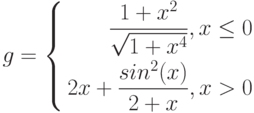
$$y=sin(x)e^{-2x}$$$$ g=\left\{ \begin{aligned} \frac{1+x^{2}}{\sqrt{1+x^{4}}}, x\leq 0 \\ 2x+\frac{sin^{2}(x)}{2+x},x>0 \end{aligned} \right. $$$$ z=\left\{ \begin{aligned} \frac{1+|x|}{\sqrt[3]{1+x+x^{2}}},x\leq-1\\ 2ln(1+x^{2}+\frac{1+cos^{4}(x)}{2+x},x\in [-1;0]\\ (1+x)^{\frac{3}{5}}, x\geq0 \end{aligned} \right. $$

2. Построить в одной системе координат при $х\in [-2; 2]$ графики функций:

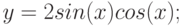
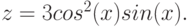
$$y = 2sin(x)cos(x);$$$$z = 3 cos^{2}(x)sin(x).$$

3. Построить поверхность 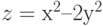$z = х^{2} – 2у^{2}$ при $x,y\in[-1; 1]$ .

Вариант 2.

1. Построить в разных системах координат при $х\in [-2; 2]$ графики функций:

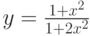
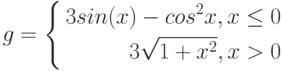
$$y=\frac{1+x^{2}}{1+2x^{2}}$$$$ g=\left\{ \begin{aligned} 3sin(x)-cos^{2}x,x\leq0\\ 3\sqrt{1+x^{2}},x>0 \end{aligned} \right. $$$$ z=\left\{ \begin{aligned} \frac{1+x}{\sqrt[3]{1+x^{2}}},x\leq0\\ -x+2e^{-2x},x\in(0,1)\\ |2-x|^{\frac{1}{3}},x\geq1 \end{aligned} \right. $$

2. Построить в одной системе координат при $х\in [-2; 2]$ графики функций:

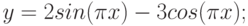
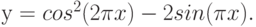
$$y=2 sin(\pi x)-3 cos(\pi x);$$$$у = cos^{2}(2\pi x)-2sin(\pi x).$$

3. Построить поверхность 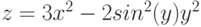$z = 3x^{2}-2sin^{2}(y)y^{2}$ при $x, y\in [-1; 1]$ .

Вариант 3.

1. Построить в разных системах координат при $x\in[-2; 1.5]$ графики функций:

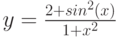
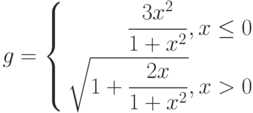
$$y=\frac{2+sin^{2}(x)}{1+x^{2}}$$$$ g=\left\{ \begin{aligned} \frac{3x^{2}}{1+x^{2}},x\leq0\\ \sqrt{1+\frac{2x}{1+x^{2}}},x>0 \end{aligned} \right. $$$$ z=\left\{ \begin{aligned} 3x+\sqrt{1+x^{2}},x<0\\ 2cos(x)e^{-2x},x\in[0,1]\\ 2sin(3x),x>1 \end{aligned} \right. $$

2. Построить в одной системе координат при $х\in [-2; 2]$ графики функций:

$$y=5sin(\pi x)-cos(3\pi x)sin(\pi x)$$$$z=cos(2\pi x)-2sin^{3}(\pi x)$$

3. Построить поверхность 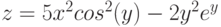$z=5x^{2}cos^{2}(y)-2y^{2}e^{y}$ при $х,y\in [-1; 1]$.

Вариант 4.

1. Построить в разных системах координат при $х\in [-1.5; 1.5]$ графики функций:

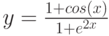
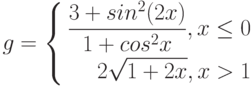
$$y=\frac{1+cos(x)}{1+e^{2x}}$$$$ g=\left\{ \begin{aligned} \frac{3+sin^{2}(2x)}{1+cos^{2}x},x\leq0\\ 2\sqrt{1+2x},x>1 \end{aligned} \right. $$$$ z=\left\{ \begin{aligned} \sqrt{1+\frac{x^{2}}{1+x^{2}}},x<0\\ 2cos^{2}(x),x\in[0,1]\\ \sqrt{1+|2sin(3x)|^{\frac{1}{3}}},x>1 \end{aligned} \right. $$

2. Построить в одной системе координат при $х\in [-2; 2]$ графики функций:

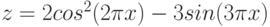
$$y=3sin(2\pi x)cos(\pi x)-cos^{2}(3\pi x);$$$$z=2cos^{2}(2\pi x)-3sin(3\pi x)$$

3. Построить поверхность при мммх,y\in [-1; 1]/ммм

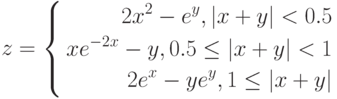
$$ z=\left\{ \begin{aligned} 2x^{2}-e^{y}, |x+y|<0.5\\ xe^{-2x}-y, 0.5\leq|x+y|<1\\ 2e^{x}-ye^{y}, 1\leq|x+y| \end{aligned} \right. $$

Вариант 5.

1. Построить в разных системах координат при $х\in [-1.8; 1.8]$ графики функций:

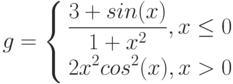
$$y=\sqrt[4]{1+e^{3x}}$$$$ g=\left\{ \begin{aligned} \frac{3+sin(x)}{1+x^{2}}, x\leq0\\ 2x^{2}cos^{2}(x), x>0 \end{aligned} \right. $$$$ z=\left\{ \begin{aligned} |x|^{\frac{1}{3}}, x<0\\ -2x+\frac{x}{1+x}, x\in[0,1]\\ \frac{|3-x|}{1+x}, x\geq1 \end{aligned} \right. $$

2. Построить в одной системе координат при $х\in [0; 3]$ графики функций:

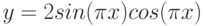
$$y=2sin(\pi x)cos(\pi x)$$$$z=cos^{2}(\pi x)sin(3\pi x)$$

3. Построить поверхность 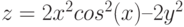$z = 2x^{2} cos^{2}(x) – 2y^{2}$ при $х,y\in [-l; 1]$.

Вариант 6.

1. Построить в разных системах координат при $х\in [-2; 1.8]$ графики функций:

$$ g=\left\{ \begin{aligned} \sqrt{1+2x^{2}-sin(x)}, x\leq0\\ \frac{2+x}{\sqrt[3]{2+e^{-0.1x}}}, x>0 \end{aligned} \right. $$$$ z=\left\{ \begin{aligned} \frac{1+x}{1+x^{2}}, x<0\\ \sqrt{1+\frac{x}{1+x}}, x\in[0,1]\\ 2|sin(3x)|, x\geq1 \end{aligned} \right. $$

2. Построить в одной системе координат при $х\in [-3; 0]$ графики функций:

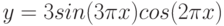
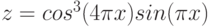
$$y=3sin(3\pi x)cos(2\pi x)$$$$z=cos^{3}(4\pi x)sin(\pi x)$$

3. Построить поверхность $z = 2е^{0.2x} х^{2} – 2у^{4}$ при $х,y\in [-1; 1]$ .

Вариант 7.

1. Построить в разных системах координат при $х\in [-1.7; 1.5]$ графики функций:

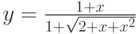
$$y=\frac{1+x}{1+\sqrt{2+x+x^{2}}}$$$$ g=\left\{ \begin{aligned} \sqrt{1+x^{2}}, x<0\\ \frac{1+x}{1+\sqrt[3]{1+e^{-0.2x}}}, x>0 \end{aligned} \right. $$$$ z=\left\{ \begin{aligned} \frac{1+x+x^{2}}{1+x^{2}}, x<0\\ \sqrt{1+\frac{2x}{1+x^{2}}}, x\in[0,1]\\ 2|0.5+sin(x)|, x\geq1 \end{aligned} \right. $$

2. Построить в одной системе координат при $х\in [-3;0]$ графики функций:

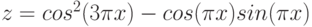
$$y=2sin(2\pi x)cos(4\pi x)$$$$z=cos^{2}(3\pi x)-cos(\pi x)sin(\pi x)$$

3. Построить поверхность 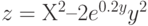$z = Х^{2} – 2e^{0.2y} y^{2}$ при $х,y\in [-1;1]$.

Вариант 8.

1. Построить в разных системах координат при $х\in [-1.5; 1.8]$ графики функций:

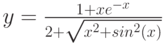
$$y=\frac{1+xe^{-x}}{2+\sqrt{x^{2}+sin^{2}(x)}}$$$$ g=\left\{ \begin{aligned} \sqrt{1+|x|}, x\leq0\\ \frac{1+3x}{2+\sqrt[3]{1+x}}, x>0 \end{aligned} \right. $$$$ z=\left\{ \begin{aligned} 1+\frac{3+x}{1+x^{2}}, x<0\\ \sqrt{1+(1-x)^{2}},x\in[0,1]\\ \frac{1+x}{1+cos^{2}(x)}, x\geq1 \end{aligned} \right. $$

2. Построить в одной системе координат при $х\in [0; 2]$ графики функций:

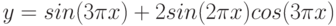
$$y=sin(3\pi x)+2sin(2\pi x)cos(3\pi x)$$$$z=cos(\pi x)-cos(3\pi x)sin^{2}(\pi x)$$

3. Построить поверхность при $х,y\in [-1; 1]$

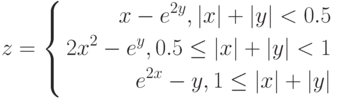
$$ z=\left\{ \begin{aligned} x-e^{2y}, |x|+|y|<0.5\\ 2x^{2}-e^{y}, 0.5\leq|x|+|y|<1\\ e^{2x}-y, 1\leq|x|+|y| \end{aligned} \right. $$

Вариант 9.

1. Построить в разных системах координат при $х\in [-1.4; 1.9]$ графики функций:

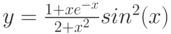
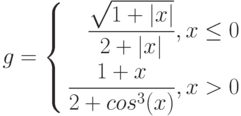
$$y=\frac{1+xe^{-x}}{2+x^{2}}sin^{2}(x)$$$$ g=\left\{ \begin{aligned} \frac{\sqrt{1+|x|}}{2+|x|}, x\leq0\\ \frac{1+x}{2+cos^{3}(x)}, x>0 \end{aligned} \right. $$$$ z=\left\{ \begin{aligned} \frac{1+2x}{1+x^{2}}, x<0\\ sin^{2}(x)\sqrt{1+x},x\in[0,1]\\ sin^{2}(x)e^{0.2x}, x\geq1 \end{aligned} \right. $$

2. Построить в одной системе координат при $х\in [0;2]$ графики функций:

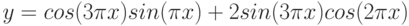
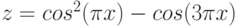
$$y=cos(3\pi x)sin(\pi x)+2sin(3\pi x)cos(2\pi x)$$$$z=cos^{2}(\pi x)-cos(3\pi x)$$

3. Построить поверхность при $х,y\in [-1; 1]$$

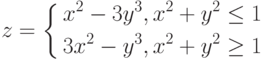
$$ z=\left\{ \begin{aligned} x^{2}-3y^{3},x^{2}+y^{2}\leq1\\ 3x^{2}-y^{3},x^{2}+y^{2}\geq1 \end{aligned} \right. $$

Вариант 10.

1. Построить в разных системах координат при $х\in [-1.4; 1.4]$ графики функций:

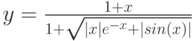
$$y=\frac{1+x}{1+\sqrt{|x|e^{-x}+|sin(x)|}}$$$$ g=\left\{ \begin{aligned} \sqrt[3]{1+x^{2}}, x\leq0\\ sin^{2}(x)+\frac{1+x}{1+cos^{2}(x)}, x>0 \end{aligned} \right. $$$$ z=\left\{ \begin{aligned} \frac{|x|}{1+x^{2}}e^{-2x}, x<0\\ \sqrt{1+x^{2}},x\in[0,1]\\ \frac{1+sin(x)}{1+x}+3x, x\geq1 \end{aligned} \right. $$

2. Построить в одной системе координат при $х\in [0; 2]$ графики функций:

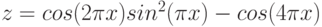
$$y=2sin(2\pi x)cos(\pi x)+sin(3\pi x)$$$$z=cos(2\pi x)sin^{2}(\pi x)-cos(4\pi x)$$

3. Построить поверхность z = 3x2sin2(x) – 5e2yу при $х,y\in [-1; 1]$ .

КОНТРОЛЬНЫЕ ВОПРОСЫ

  1. Из каких этапов состоит процесс построения графика функции?
  2. Какими способами можно ввести в ячейки диапазона ряд последовательных значений, образующих арифметическую прогрессию?
  3. Как подписать ось X значениями аргумента?
Дальше >>
< Лекция 3 || Лекция 4 || Лекция 5 >

Вопросы и ответы

вопросов: 1
Арсен Никифоров
Арсен Никифоров
Как правильно заполнять последовательность ответов?
ответить

Студенты

всего: 980
Марианна Дербенева
Марианна Дербенева
Россия, СПБГУЭФ, 2008
предложить дружбу
Камиль Гарипов
Камиль Гарипов
Россия, Арск
предложить дружбу