Метод проб
Рассмотрим произвольную ДНФ. Если в ней выбросить любое произведение, то оставшееся выражение будет принимать нулевое значение на тех наборах, что и исходная форма, т.к.  только тогда все члены
только тогда все члены  .
.
Однако, если отброшенное произведение (импликанта) обращалось в единицу, и функция принимала единичное значение на этом единственном наборе, то оставшееся выражение может уже не принять единичное значение на данном наборе. Это означает, что импликанта не была лишней. Если же с помощью проверки установить, что оставшееся выражение обращается в единицу, импликанта – лишняя, и ее можно отбросить.
Пример 1:
Пусть дана 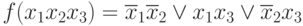
-
Отбросим член x1x2:

x1x2 = 1 => x1 = 0, x2 = 0

Т.к.
 то x1x2 исключить нельзя
то x1x2 исключить нельзя -
Отбросим член x1x3:

x1x3 = 1 => x1 = 1, x3 = 1

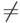 1 => x1x3 исключить нельзя.
1 => x1x3 исключить нельзя. - Отбросим член x2x3:

x2x3 = 1 => x2 = 0, x3 = 1
 => x2x3 - член лишний.
=> x2x3 - член лишний.
Если проверка показывает, что несколько импликант одновременно являются лишними, то исключить их одновременно из выражения ДНФ нельзя. Это можно выполнять лишь поочередно.
Пример 2:

- испытаем 1 член: x1x3x4 = 1; x1 = 0; x3 = 1; x4 = 1
 Т.е. член x1x3x4 исключить нельзя.
Т.е. член x1x3x4 исключить нельзя. - испытаем 2 член: x2x3x4 = 1; x2 = 0; x3 = x4 = 1
 Т.е. член x2x3x4 лишний.
Т.е. член x2x3x4 лишний. - испытаем 3 член: x1x2x4 ; x1 = 1; x2 = 0 x4 = 1
 Т.е. член x1x2x4 лишний.
Т.е. член x1x2x4 лишний. - испытаем 4 член: x1x2x3 ; x1 = 1; x2 = x3 = 0
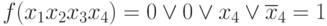 , Т.е. член x1x2x3 лишний.
, Т.е. член x1x2x3 лишний. - испытаем 5 член: x2x3x4 ; x2 = x3 = x4 = 0
 , Т.е. член x2x3x4 не лишний.
, Т.е. член x2x3x4 не лишний.
Исключим одновременно члены 2, 3, 4

Проверим значения f одновременно на тех наборах, на которых обращаются в единицу все отброшенные члены.

т.е. видно, что во всей совокупности этого сделать нельзя
Исключим член x2x3x4, получим:

Проверим, не являются ли в этом выражении лишними те члены, которые оказались лишними в исходном выражении, т.е.: x1x2x4 и x1x2x3.
- проверим x1x2x4:
x1 = 1; x2 = 0; x4 = 1
 т.е. член x1x2x4 не лишний
т.е. член x1x2x4 не лишний - проверим x1x2x3:
x1 = 1; x2 = x3 = 0
 , т.е. член x1x2x3 лишний,
, т.е. член x1x2x3 лишний,
Поэтому  - тупиковая форма.
- тупиковая форма.
Проверяя затем, начав с исключения третьего члена, получим другую тупиковую форму. Затем выберем из них минимальную.
Недостаток метода заключается в том, что при большом числе членов он становится громоздким, поскольку связан с перебором различных вариантов. Машинная реализация данного метода вследствие этого сложна. При автоматизации поиска минимальных форм метод практически не используется.