Визуализация пространственных реалистических сцен
Текстуры
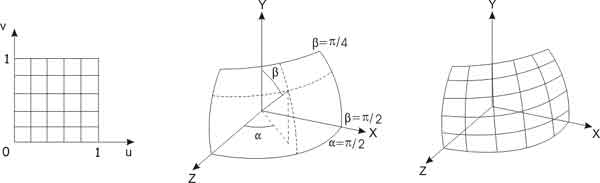
Текстура поверхности - это детализация ее строения, учитывающая микрорельеф и особенности окраски. Во-первых, гладкая поверхность может быть покрыта каким-либо узором, и тогда при ее изображении решается задача отображения этого узора на проекции фрагментов поверхности (многоугольники). Во-вторых, поверхность может быть шероховатой, поэтому нужны специальные приемы имитации такого микрорельефа при закрашивании.
Сначала рассмотрим методы отображения узоров. Чаще всего узор
задается в виде образца, заданного на прямоугольнике в декартовой
системе координат 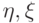 в пространстве текстуры. Фрагмент поверхности
может быть задан в параметрическом виде в трехмерной декартовой
системе координат:
в пространстве текстуры. Фрагмент поверхности
может быть задан в параметрическом виде в трехмерной декартовой
системе координат:
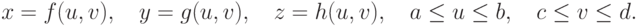
Теперь достаточно построить отображение области в пространстве текстуры в область параметров поверхности
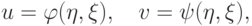

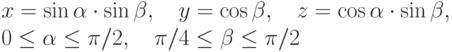
а образец текстуры задан на квадрате  . Тогда можно воспользоваться
линейным отображением вида
. Тогда можно воспользоваться
линейным отображением вида

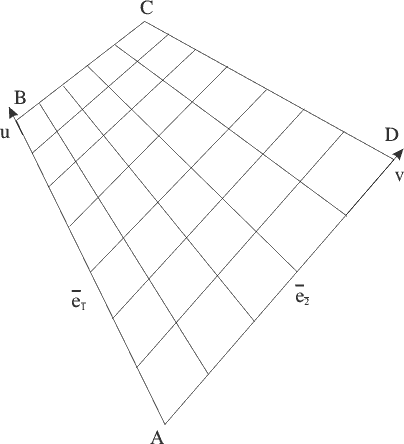
Если положить 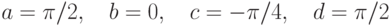 , то углы образца отобразятся в углы криволинейного
четырехугольника, как это показано на рис. 10.6.
, то углы образца отобразятся в углы криволинейного
четырехугольника, как это показано на рис. 10.6.
Обратное отображение имеет вид
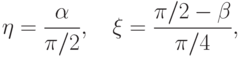
Пусть теперь нужно нанести текстуру при перспективном проецировании
произвольно ориентированной прямоугольной грани. Грань задана в
пространстве набором своих вершин 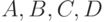 . Построим векторы
. Построим векторы 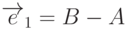 и
и 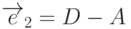 ,
направленные вдоль сторон прямоугольника. Любую точку прямоугольника
можно единственным образом представить в виде
,
направленные вдоль сторон прямоугольника. Любую точку прямоугольника
можно единственным образом представить в виде
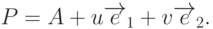
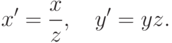
Найдем образ точки P при таком преобразовании:
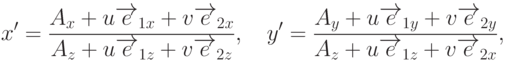

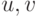 , то, решив ее, получим требуемое обратное
преобразование. Для решения можно воспользоваться, например, правилом
Крамера:
, то, решив ее, получим требуемое обратное
преобразование. Для решения можно воспользоваться, например, правилом
Крамера: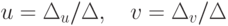
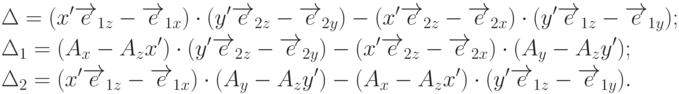
Можно рассмотреть более общий случай перспективной проекции, задаваемый соотношениями
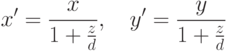
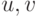 немного усложнятся:
немного усложнятся: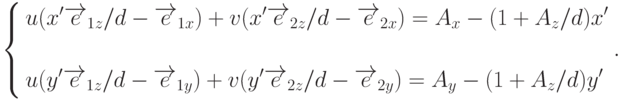
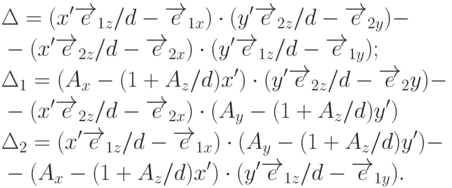
В рассмотренных примерах мы имели дело с гладкими поверхностями. Можно имитировать шероховатость путем выбора подходящего образца нерегулярной текстуры, но все равно изображение будет выглядеть так, словно неоднородности нанесены на гладкой поверхности. Для моделирования микрорельефа Дж.Блин предложил метод, основанный на возмущении нормали к поверхности.
Пусть, как и ранее, поверхность задана в параметрическом виде с
помощью векторной функции 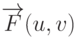 . В каждой ее точке можно построить вектор
нормали, воспользовавшись частными производными этой функции.
Известно, что производные
. В каждой ее точке можно построить вектор
нормали, воспользовавшись частными производными этой функции.
Известно, что производные 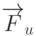 и
и 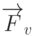 представляют собой векторы, лежащие в
касательной плоскости данной поверхности. Тогда вектор нормали может
быть получен как векторное произведение этих двух векторов
представляют собой векторы, лежащие в
касательной плоскости данной поверхности. Тогда вектор нормали может
быть получен как векторное произведение этих двух векторов  . После
этого точку поверхности можно отклонить от первоначального положения в
направлении нормали на некоторую малую величину, задаваемую с помощью
функции возмущения
. После
этого точку поверхности можно отклонить от первоначального положения в
направлении нормали на некоторую малую величину, задаваемую с помощью
функции возмущения  :
:

Можно показать, что нормаль к новой возмущенной поверхности будет определяться выражением
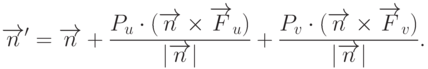
Вопросы и упражнения
- Какие этапы выделяются в свето-теневом анализе?
- К какому типу относится алгоритм Аппеля: итеративному или рекурсивному?
- Возможно ли использование алгоритма Аппеля для сцен с неполным затенением?
- Что такое теневой буфер? Чем он отличается от традиционного Z-буфера?
- В чем состоит модификация алгоритма Вейлера-Азертона для выполнения свето-теневого анализа?
- В какой модели освещенности можно использовать метод излучательности?
- Чем отличается трассировка лучей в глобальной модели освещенности от метода удаления невидимых граней?
- Какие составляющие интенсивности рассматриваются в методе трассировки?
- Каким образом можно использовать двоичные деревья в алгоритме трассировки?
- Какой способ задания поверхности наиболее удобен для текстурирования?
- В чем состоит идея моделирования микрорельефа при нанесении текстур?