Микропроцессорные системы и способы распараллеливания
Второй способ распараллеливания — по информации — используется тогда, когда можно распределить обрабатываемую информацию между процессорами для обработки по идентичным алгоритмам (по одному алгоритму).
1. Рассмотрим задачу умножения матриц 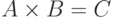 :
:
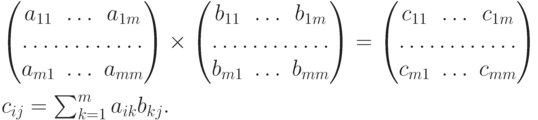
Развернем матрицу — результат  — в линейный
(одномерный) массив, переименуем ее элементы и заменим два индекса на один:
— в линейный
(одномерный) массив, переименуем ее элементы и заменим два индекса на один:

Пусть ВС содержит n процессоров. Выберем следующий план счета элементов матрицы C:
процессор 1 считает элементы d1, d1+n, d1+2n, ...
процессор 2 считает элементы d2, d2+n, d2+2n, ...
........................................................................
процессор n считает элементы dn, d2n, d3n, ...
По-видимому, все они будут выполнять одну и ту же программу, но обрабатывать разные наборы данных. (Мы снова столкнулись с целесообразностью SPMD -технологии.)
Здесь не потребовалась какая-либо синхронизация параллельного вычислительного процесса.
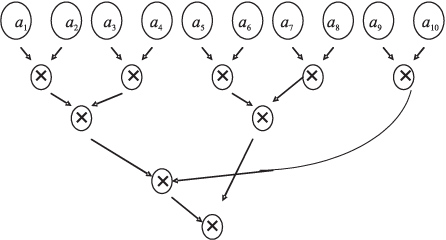
2. Рассмотрим задачу счета способом "пирамиды".
Эту задачу мы исследовали при рассмотрении ВС типа SPMD. Посмотрим еще раз, какая синхронизация нам здесь потребуется.
Пусть необходимо перемножить все элементы некоторого массива {a1,a2,... , a10}. Каждый элемент занимает одну ячейку памяти. Пусть число процессоров в ВС n=4. Чтобы распараллелить этот процесс, примем схему счета "пирамидой" (рис. 2.7).
Количество уровней операций в ней ]log2 m[=]log210[=4 ( ]x[ — ближайшее целое, не меньшее x ).
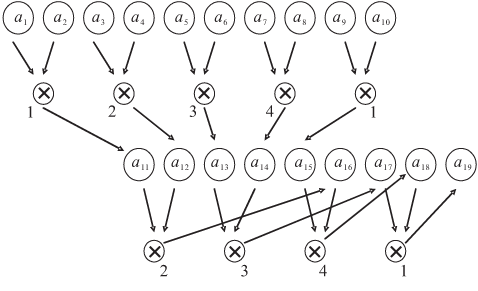
Расширим массив, дополнив его ячейками, в которых будем хранить промежуточные частные произведения. Тогда весь план счета примем таким, как показано на рис. 2.8. Отмечены процессоры, выполняющие указанную операцию.
Следовательно, надо так написать программу, одну для всех процессоров, предусмотрев необходимую переадресацию для выборки и вычисления "своих" данных, чтобы по ней выбирались два соседних элемента этого удлиненного массива, а результат их умножения отправлялся в очередную ячейку этого "удлинения".
Возникает только одна трудность: для первых пяти произведений данные есть, а вот последующие произведения должны выполняться тогда, когда для них будут найдены исходные данные.
Значит, процессоры, которым выпало произвести такие умножения, должны "уметь" обнаруживать отсутствие данных и дожидаться их появления. Т.е. требуется синхронизация процессоров по использованию общих данных.
Здесь распараллеливание по данным смыкается с распараллеливанием по управлению.
Возможная схема общей для всех процессоров программы — на рис. 2.9. Она реализована в примере для ВС типа SPMD.