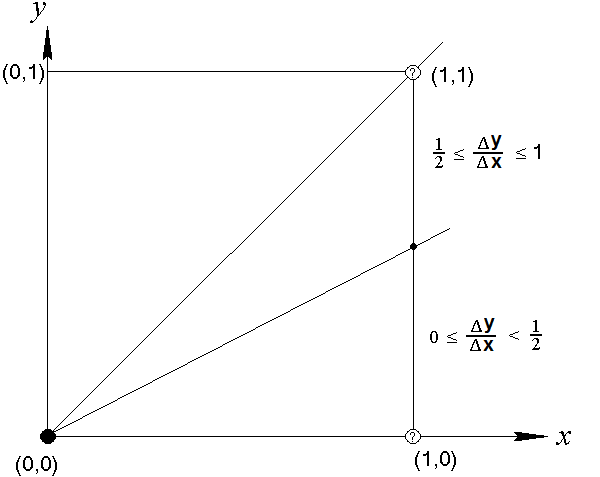Растровое преобразование графических примитивов

Экран растрового дисплея можно рассматривать как матрицу дискретных элементов, или пикселей. Процесс определения пикселей, наилучшим образом аппроксимирующих некоторую геометрическую фигуру, называется разложением в растр, или построением растрового образа фигуры. Построчная визуализация растрового образа называется растровой разверткой данной фигуры.

Алгоритм Брезенхема растровой дискретизации отрезка

При построении растрового образа отрезка необходимо, прежде всего, установить критерии "хорошей" аппроксимации. Первое требование состоит в том, что отрезок должен начинаться и кончаться в заданных точках и при этом выглядеть сплошным и прямым (при достаточно высоком разрешении дисплея этого можно добиться). Кроме того, яркость вдоль отрезка должна быть одинаковой и не зависеть от наклона отрезка и его длины. Это требование выполнить сложнее, поскольку горизонтальные и вертикальные отрезки всегда будут ярче наклонных, а постоянная яркость вдоль отрезка опять же достигается на вертикальных, горизонтальных и наклоненных под углом в 45 линиях. И, наконец, алгоритм должен работать быстро. Для этого необходимо по возможности исключить операции с вещественными числами. С целью ускорения работы алгоритма можно также реализовать его на аппаратном уровне.

Рис. 8.1. Растровый образ отрезка

В большинстве алгоритмов используется пошаговый метод изображения, т.е. для нахождения координат очередной точки растрового образа наращивается значение одной из координат на единицу растра и вычисляется приращение другой координаты.

Задача состоит в построении отрезка, соединяющего на экране точки с координатами 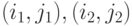(будем считать, что 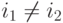). Для построения отрезка прямой на плоскости с вещественными координатами можно воспользоваться уравнением прямой, проходящей через две заданные точки, которое имеет вид

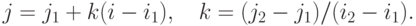
Теперь, считая, что 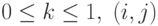- координаты текущей точки растрового образа, а - точное значение координаты точки отрезка, можно построить следующую точку:

Следует заметить, что целочисленная координата изменится только в том случае, если y превысит величину 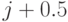( 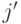есть ближайшее к целое число, полученное в результате операции округления). Приведенный пример включает операции с вещественными числами, которые выполняются существенно медленнее, чем соответствующие целочисленные операции, а при построении растрового образа отрезка желателен алгоритм, по возможности обращающийся только к целочисленной арифметике. Кроме того, алгоритм должен работать при любом взаимном расположении концов отрезка.

Алгоритм Брезенхема построения растрового образа отрезка был изначально разработан для графопостроителей, но он полностью подходит и для растровых дисплеев. В процессе работы в зависимости от углового коэффициента отрезка наращивается на единицу либо , либо , а изменение другой координаты зависит от расстояния между действительным положением точки и ближайшей точкой растра (смещения). Алгоритм построен так, что анализируется лишь знак этого смещения.

Рис. 8.2. Связь углового коэффициента с выбором пикселя

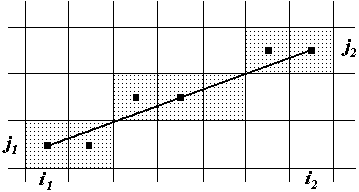
На рис. 8.2 это иллюстрируется для отрезка с угловым коэффициентом, лежащим в диапазоне от нуля до единицы. Из рисунка можно заметить, что если угловой коэффициент 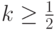, то при выходе из точки 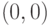пересечение с прямой 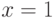будет ближе к прямой 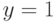, чем к прямой . Следовательно, точка растра 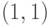лучше аппроксимирует прохождение отрезка, чем точка 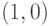. При 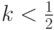верно обратное.

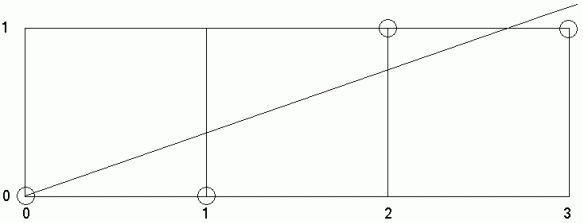
На рис. 8.3 показано, каким образом строятся точки растра для отрезка с тангенсом угла наклона 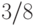, а на рис. 8.4 - график смещения. В начале построения смещение полагается равным 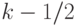, а затем на каждом шаге оно наращивается на величину , и если при этом вертикальная координата точки растра увеличивается на единицу, то смещение в свою очередь уменьшается на единицу.

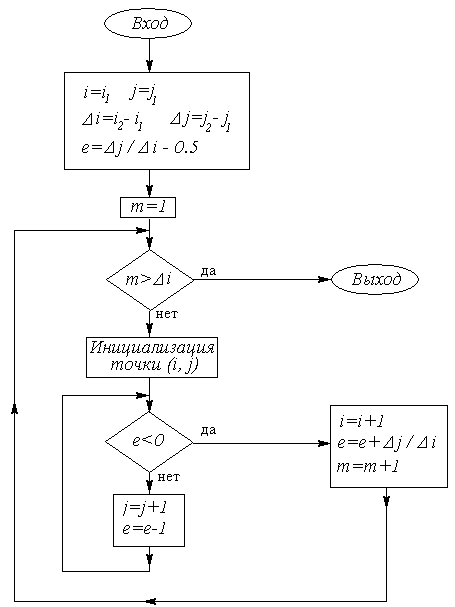
На рис. 8.5 приведена блок-схема алгоритма для случая 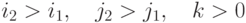. Нетрудно понять, как от этого алгоритма перейти к целочисленному: достаточно вместо величины смещения перейти к величине .

Рис. 8.3. Пиксели, принадлежащие развертке отрезка

Рис. 8.4. График изменения отклонения

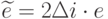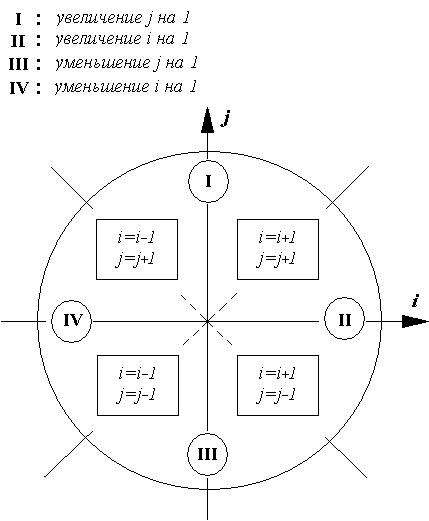
Приведем общий алгоритм Брезенхема, который учитывает все возможные случаи направления отрезка, рассматриваемого как вектор на координатной плоскости (на рис. 8.6 выделены четыре области и указаны особенности алгоритма в каждой из них).

В описании алгоритма используются следующие функции:

swap (a, b): обмен значений переменных a, b;
abs (a): абсолютное значение a;
sign (a): 0, если a= 0, 1, если a>0, –1, если a<0;
point (i, j) - инициализация точки (i, j).

Предполагается, что концы отрезка 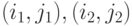не совпадают и что все используемые переменные являются целыми.

Рис. 8.5. Блок-схема одной ветви алгоритма Брезенхема

i=i1;
j=j1;
di=i2-i1;
dj=j2-j1;
s1=sign(i2-i1);
s2=sign(j2-j1);
di=abs(di);
dj=abs(dj);
if (dj>di) 
{
 swap(di,dj); c=1;
} 
else c=0;
e=2*dj-di;	// Инициализация смещения
// Основной цикл
for (l=0; l<di; l++)
{
	point(i,j);
	while (e>=0)
	{ 
		if (c==1) i=i+s1; 
		else j=j+s2;
		e=e-2*di;
	}
	if (c==1) j=j+s2; else i=i+s1;
	e=e+2*dj;
	}

Рис. 8.6. Четыре возможных направления отрезка