Инструменты, алгоритмы и структуры данных
[+]
Опубликован: 06.10.2011 | Доступ: свободный | Студентов: 1678 / 102 | Оценка: 4.67 / 3.67 | Длительность: 18:18:00
Тема: Программирование
Специальности: Программист, Системный архитектор
Теги: eiffel, java, tuple, алгоритмы, ациклический, библиотеки, БНФ, вычисления, клиенты, компиляторы, левое поддерево, нетерминал, программирование, процедуры, рекурсивный метод, структуры данных, топологическая сортировка, транзитивное замыкание, указатели, универсальный класс, элементы
Лекция 6:

Фундаментальные структуры данных, универсальность и сложность алгоритмов
A
|
версия для печати
< Лекция 5 || Лекция 6: 12345 || Лекция 7 >

5.3. Оценка алгоритмической сложности

Последний комментарий поднимает проблему эффективности (производительности), которая включает как время выполнения, так и требуемый объем памяти. Главная причина использования различных видов контейнеров состоит в том, что они обладают разной эффективностью по памяти и времени, зависящей от выполняемых над контейнером операций.

Необходим надежный способ сравнения производительности для выбора нужного типа контейнера. Недостаточно провести эксперименты над конкретным контейнером и сделать вывод, что "в среднем запрос на вызов элемента требует 10 наносекунд при работе с массивом и 40 наносекунд при работе со связным списком".

  • Корректные рассуждения "о средних" требуют знания статистического распределения. Для размеров контейнеров трудно ожидать разумного определения такого распределения (сколько контейнеров может быть с 10 элементами, сколько с 1000 элементами и т. д.).
  • Нельзя полагаться на результаты измерений из-за проблем масштабирования. Некоторые методы прекрасно работают для небольших размеров структуры, но становятся критическими для больших структур.
  • Результаты измерений существенно зависят от окружения – компьютера, операционной системы, даже от языка программирования и компилятора; те же эксперименты в другом окружении могут дать принципиально различные результаты.

Основной способ оценки сложности алгоритмов свободен от таких привходящих обстоятельств. Он известен как абстрактная сложность, а также как асимптотическая сложность или нотация "О-большое".

Измерение порядка величин

Абстрактная сложность основывается на двух принципах.

  • Рассматривает меру сложности как функцию от размера структуры данных. Для большинства примеров этой лекции размер задается одним параметром – count – числом элементов контейнера.
  • Функция определяется не точной формулой, а порядком величины, задаваемой нотацией "О-большое", как O(count).

Когда мы говорим, что время поиска элемента в списке из count элементов составляет O(count), это означает, что с ростом count оно возрастает, в худшем случае, пропорционально count. Другая операция может иметь время 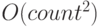O(count^2), означающее, что время возрастает самое большее пропорционально квадрату числа элементов. Те же соглашения действуют при оценке требуемой памяти.

Для такой меры:

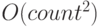  • константные мультипликативные множители не играют роли: O(100* count^2) означает то же самое, что и O(count^2). Объяснение этого соглашения состоит в том, что не следует придавать большого значения умножению на константу, так как реализация того же алгоритма может быть в сто раз быстрее или медленнее, будучи перенесенной на другую машину. Но рост времени вычислений при изменении count не зависит от таких технических деталей;
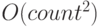  • понятно, что не имеет значения и константная аддитивная составляющая: O(count^2 + 1000) означает то же самое, что и O(count^2). Конечно, константа может оказывать влияние при небольших значениях count, но с его ростом влияние становится ничтожным;
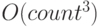  • аналогично: любая аддитивная составляющая с меньшим значением экспоненты также не оказывает влияния на порядок величины – O(count^3 + count^2) означает то же самое, что и O(count^3).

Как следствие, чтобы выразить тот факт, что алгоритм работает константное время, более точно – что на любой платформе время выполнения ограничено константой, будем говорить, что время работы O(1). Конечно с тем же успехом можно писать O(37) или O(1000), но принято писать O(1).

Математические основы

Нотация "О-большое" может показаться неформальной, но ее можно строго определить, как отношение между функциями.

Определение: нотация "О-большое" и абстрактная сложность
Пусть f и g – две функции над натуральными числами, задающие отображение в положительные вещественные числа. Говорят, что f есть O (g) – или, в более общем виде, f (n) является O (g (n)), указывая аргумент, – если существует константа K, такая, что f (n) / g (n)< K для каждого натурального числа n.

Алгоритм является O (g (n)) по времени или по памяти, если функция, задающая время выполнения или требуемый объем памяти при входном размере n, есть O (g (n)).

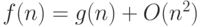При анализе сложности алгоритма можно встретиться с таким выражением, как "f (n) = g (n) + O (n^2)", что является сокращением записи "f (n) = g (n) + s (n) для некоторой функции s, где s (n) есть 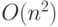O (n^2)". Тем самым устанавливается, что f "подобна" g, отличаясь на терм O (n^2).

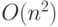Следствием определения является тот факт, что если функция есть 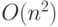O (n^2), то верно, что она есть также 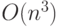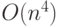O (n^3), O (n^4) и так далее. Это потому, что О-большое задает верхнюю границу, а не представляет точную оценку. Полезные утверждения, связанные со сложностью, часто имеют вид: "Доказано, что сложность данного алгоритма есть 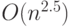O (n^{2.5}). Можно ли улучшить оценку и доказать, что его сложность есть O (n^2)?"

В теории сложности алгоритмов применяется нотация Тета-большое (θ(g (n))) в тех случаях, когда функция g асимптотически обеспечивает как нижнюю, так и верхнюю границу с разными константными мультипликативными множителями. Для простоты мы будем использовать нотацию О-большое, предполагая при этом, что функции g на данном этапе рассмотрения являются наилучшими из известных, характеризуя поведение алгоритма в наихудших условиях.

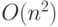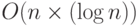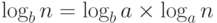При анализе сложности алгоритмов часто возникают логарифмы. Например, лучшие алгоритмы сортировки списка из n элементов имеют сложность O(n\times(\log n)). В этой формуле не указывается основание системы логарифмов (2 или 10), поскольку изменение основания приводит к появлению мультипликативной константы \log_b n=\log_b a\times\log_a n.

Лучшее использование выигрыша в лотерею

Соглашение об игнорировании мультипликативной константы на первый взгляд кажется удивительным. Алгоритм, работающий count^2 наносекунд, считается хуже алгоритма, работающего 10^6 * count наносекунд, хотя последний работает быстрее при count меньше миллиона.

Следующее наблюдение позволяет понять преимущества алгоритмов, лучших по сложности. Рассмотрим четыре алгоритма, каждый из которых, непрерывно работая на вашем компьютере, за 24 часа может решить задачу максимальной размерности соответственно 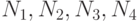N_1, N_2, N_3, N_4. Предположим теперь, что алгоритмическая сложность наших алгоритмов соответственно составляет 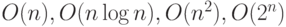O(n), O(n \log n), O(n^2), O(2^n). Предположим еще (что менее вероятно), что вы выиграли в лотерею большую сумму и можете купить новый компьютер, работающий в 1000 раз быстрее старого. Что это может вам дать?

Для первого алгоритма со сложностью O(n) теперь можно будет решить задачу в 1000 раз большего размера – 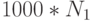1000 * N_1.

Для второго алгоритма со сложностью 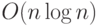O(n \log n) теперь можно будет решить задачу большего размера с множителем, близким к 1000.

Для третьего алгоритма со сложностью 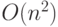O(n^2) теперь можно будет решить задачу большего размера с существенно меньшим множителем, равным квадратному корню из 1000, примерно равным 32.

Для четвертого алгоритма увеличение размера почти неощутимо, размер задачи увеличится на 10 (не в 10 раз, а на 10!).

Правильный вопрос, который нужно задавать при анализе сложности алгоритма, – не "каково время решения задачи", а "насколько большую задачу можно решить данным алгоритмом за фиксированное время при увеличении скорости работы компьютера".

Рассмотрим в качестве примера программу, дающую ежедневный прогноз погоды. Благодаря компьютерному моделированию метеорологи добились серьезных успехов за последние два десятилетия. Прогноз дается по данным, собранным в различных точках географической сетки. Чем больше точек сетки учитывается, тем точнее прогноз. Рассматривая эффективность программы прогноза, следует в качестве критерия брать не время расчета прогноза для фиксированного множества точек (точный прогноз на следующий день бесполезен, если он считается 48 часов), а число точек сетки, которые можно учесть при фиксированном времени расчета, скажем, за час.

Абстрактная сложность дает нам взгляд на эффективность алгоритма, свободный от технических деталей, и позволяет оценить преимущества его потенциального улучшения.

Абстрактная сложность на практике

Говоря об абстрактной сложности, чаще всего рассматривают три разных варианта, особенности каждого из которых следует четко понимать.

Средняя сложность, ожидаемое среднее время или требуемый в среднем объем памяти алгоритма. Как отмечалось ранее, говорить о среднем можно только в предположении о существовании случайного распределения для входов программы. Обычно среднюю сложность считают в предположении, что все входы равновероятны (например, при сортировке массива из n элементов можно считать, что все n! возможных упорядочений элементов могут появляться с равной вероятностью).

Максимальная сложность, также называемая сложностью в худшем случае, дающая время или память для случая, на котором алгоритм работает дольше всего (требует максимальной памяти).

Минимальная сложность, также называемая сложностью в лучшем случае, дающая время или память для случая, на котором алгоритм работает быстрее всего (требует минимальной памяти). Этот критерий используется редко – его любят те, кто верит в удачу.

Презентация структур данных

В оставшейся части лекции будем рассматривать фундаментальные структуры данных. Их презентация основана на библиотеке EiffelBase, содержащей повторно используемые классы для всех изучаемых понятий: ARRAY, LINKED_LIST, HASH_TABLE, STACK и так далее.

Описание дается в ориентации на клиента-программиста, того, кто будет использовать библиотечные классы в собственном приложении. По этой причине методы будут вводиться в их контрактном облике. Презентация объясняет базисные способы реализации; как правило, сама реализация не дается, но с ней при желании можно познакомиться, поскольку EiffelBase является библиотекой с открытым кодом, одна из целей которой состоит в предоставлении надежных образцов ОО-стиля программирования, проверенных в течение многих лет использования.

Дальше >>
< Лекция 5 || Лекция 6: 12345 || Лекция 7 >

Вопросы и ответы

вопросов: 0