Клеточная модель "Игра Жизнь" Дж.Конвея
Задания
- Реализуйте Windows-приложение, которое последовательно отображает состояния клеточной модели "Игра жизнь".
- Реализуйте последовательный алгоритм расчета состояний модели.
- Реализуйте параллельные алгоритмы расчета состояний модели. Для распараллеливания используйте задачи (tasks) или метод Parallel.For.
- Реализуйте возможность отмены расчета с помощью объекта CancellationToken.
- Выполните анализ эффективности разработанных алгоритмов.
Методические указания
Клеточная модель представляет собой множество клеток (ячеек таблицы), принимающих одно из нескольких состояний. Состояние каждой клетки определяется состоянием её ближайших соседей. Одной из известных моделей является "Игра Жизнь" математика Дж. Конвея.
В модели Конвея каждая клетка может находиться в двух состояниях: живая или неживая. Состояние клетки на следующем шаге определяется потенциалом клетки (числом живых соседних клеток):
- если потенциал клетки равен двум, то клетка сохраняет свое состояние;
- если потенциал равен трем, то клетка оживает;
- если потенциал меньше двух или больше трех, то клетка погибает.
Правила изменения состояния клетки можно описать следующим лямбда-выражением:
var lifeRules = new Func<int, bool, bool>((p, state) =>
{
if(p == 3)
return true;
else if (p == 2)
return state;
else
return false;
});
Последовательный алгоритм расчета представляет собой расчет состояния каждой клетки
LifeTable tableNew = new LifeTable;
for(int i=0; i < Height; i++)
for(int j=0; j < Width; j++)
{
p = CalcPotential(table[i,j]);
tableNew[i, j] = lifeRules(p, table[i, j]);
}
table = tableNew;
Потенциал клетки вычисляется по восьми ближайшим соседям клетки.
int CalcPotential(int i, int j)
{
int p=0;
for(int x = i-1; x <= i + 1; x++)
for(int y = j-1; y <= j + 1;y++)
{
if(x < 0 || y < 0 || x >= Height || y >= Width
|| (x == i && y == j))
continue;
if(table[x,y]) p++;
}
return p;
}
Вычисления новых состояний для каждой клетки являются независимыми и могут выполняться параллельно.
Parallel.For(0, Height, (i) => {
for(int j=0; j < Width; j++)
{
p = CalcPotential(table[i,j]);
tableNew[i, j] = lifeRules(p, table[i, j]);
}
});
Также можно изменить порядок расчета и распараллелить внешний цикл по столбцам:
Parallel.For(0, Width, (j) => {
for(int i=0; i < Height; i++)
{
p = CalcPotential(table[i,j]);
tableNew[i, j] = lifeRules(p, table[i, j]);
}
}
Вывод таблицы состояний клеточной модели может быть следующим:
Вопросы и упражнения
- Имеет ли смысл распараллеливание внутреннего цикла расчета? Почему?
for(int i=0; i < Height; i++) { Parallel.For(0, Width, j => { p = CalcPotential(table[i,j]); tableNew[i, j] = lifeRules(p, table[i, j]); }); } - Как вариант расчета – по строкам или по столбцам – более эффективен и с чем это связано?
- Продумайте вариант блочной декомпозиции, где блок выступает матрицей размера
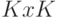 . В чем достоинства и недостатки блочной декомпозиции для этой задачи? Какое значение параметра
. В чем достоинства и недостатки блочной декомпозиции для этой задачи? Какое значение параметра  следует выбирать?
следует выбирать?

