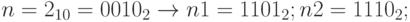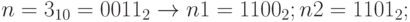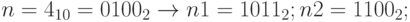|
Не очень понятно про оболочечные Данные,ячейки памяти могут наверно размер менять,какое это значение те же операции только ячейки больше,по скорости тоже самое |
Работа с числами в языке Java
Двоичное представление отрицательных целых чисел. Дополнительный код
Старший бит в целых без знака имеет обычный смысл, в целых со знаком – для положительных чисел всегда равен 0. В отрицательных числах старший бит всегда равен 1. В примерах для простоты мы будем рассматривать четырехбитную арифметику. Тогда в качестве примера целого положительного числа можно привести  .
.
Для хранения отрицательных чисел используется дополнительный код. Число (– n), где n положительно, переводится в число 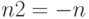 по следующему алгоритму:
по следующему алгоритму:
- этап 1: сначала число n преобразуется в число n1 путем преобразования
 , во время которого все единицы числа n заменяются нулями, а нули единицами, то есть
, во время которого все единицы числа n заменяются нулями, а нули единицами, то есть 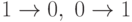 ;
; - этап 2: перевод
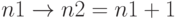 , то есть к получившемуся числу
, то есть к получившемуся числу 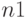 добавляется единица младшего разряда.
добавляется единица младшего разряда.
Надо отметить, что дополнительный код отрицательных чисел зависит от разрядности.
Например, код числа (–1) в четырехразрядной арифметике будет  , а в 8-разрядной арифметике будет
, а в 8-разрядной арифметике будет 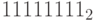 . Коды числа (–2) будут
. Коды числа (–2) будут  и
и 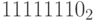 , и так далее.
, и так далее.
Для того, чтобы понять причину использования дополнительного кода, рассмотрим сложение чисел, представленных в дополнительном коде.
Сложение положительного и отрицательного чисел
Рассмотрим, чему равна сумма числа 1 и числа –1, представленного в дополнительном коде. Сначала переведем в дополнительный код число –1. При этом 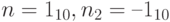 .
.
- Этап1:
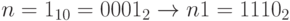 ;
; - Этап2:
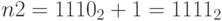 ;
;
Таким образом, в четырехбитном представлении 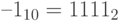 .
.
Проверка:
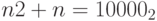 . Получившийся пятый разряд, выходящий за пределы четырехбитной ячейки, отбрасывается, поэтому в рамках четырехбитной арифметики получается
. Получившийся пятый разряд, выходящий за пределы четырехбитной ячейки, отбрасывается, поэтому в рамках четырехбитной арифметики получается 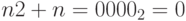 .
.
Аналогично
Очевидно, во всех этих случаях 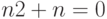 .
.
Что будет, если мы сложим 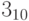 и
и  (равное 1110_2, как мы уже знаем)?
(равное 1110_2, как мы уже знаем)?
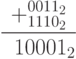
После отбрасывания старшего бита, выходящего за пределы нашей четырехбитовой ячейки, получаем 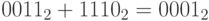 , то есть
, то есть  , как и должно быть.
, как и должно быть.
Сложение отрицательных чисел
 из-за отбрасывания лишнего старшего бита, выходящего за пределы ячейки. Поэтому
из-за отбрасывания лишнего старшего бита, выходящего за пределы ячейки. Поэтому 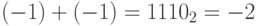 .
.
Вычитание положительных чисел осуществляется путем сложения положительного числа с отрицательным, получившимся из вычитаемого в результате его перевода в дополнительный код.
Приведенные примеры иллюстрируют тот факт, что сложение положительного числа с отрицательным, хранящимся в дополнительном коде, или двух отрицательных, может происходить аппаратно (что значит очень эффективно) на основе крайне простых электронных устройств.
Проблемы целочисленной машинной арифметики
Несмотря на достоинства в двоичной машинной (аппаратной) арифметике имеются очень неприятные особенности, возникающие из-за конечной разрядности машинной ячейки.
Проблемы сложения положительных чисел
Пусть 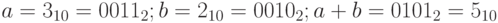 , то есть все в порядке.
, то есть все в порядке.
Пусть теперь 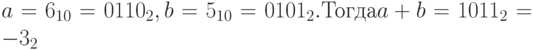 .
.
То есть сложение двух положительных чисел может дать отрицательное, если результат сложения превышает максимальное положительное число, выделяемое под целое со знаком для данной разрядности ячеек! В любом случае при выходе за разрешенный диапазон значений результат оказывается неверным.
Если у нас беззнаковые целые, проблема остается в несколько измененном виде. Сложим  в двоичном представлении. Поскольку
в двоичном представлении. Поскольку 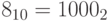 , тогда
, тогда 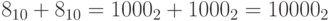 . Но лишний бит отбрасывается, и получаем 0. Аналогично в четырехбитной арифметике,
. Но лишний бит отбрасывается, и получаем 0. Аналогично в четырехбитной арифметике,  , и т.д.
, и т.д.
При целочисленном умножении выход за пределы разрядности ячейки происходит гораздо чаще, чем при сложении или вычитании. Например, 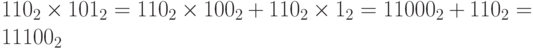 . Если наша ячейка четырехразрядная, произойдет выход за ее пределы, и мы получим после отбрасывания лишнего бита
. Если наша ячейка четырехразрядная, произойдет выход за ее пределы, и мы получим после отбрасывания лишнего бита 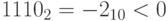 . Таким образом, умножение целых чисел легко может дать неправильный результат. В том числе – даже отрицательное число. Поэтому при работе с целочисленными типами данных следует обращать особое внимание на то, чтобы в программе не возникало ситуаций арифметического переполнения. Повышение разрядности целочисленных переменных позволяет смягчить проблему, хотя полностью ее не устраняет. Например, зададим переменные
. Таким образом, умножение целых чисел легко может дать неправильный результат. В том числе – даже отрицательное число. Поэтому при работе с целочисленными типами данных следует обращать особое внимание на то, чтобы в программе не возникало ситуаций арифметического переполнения. Повышение разрядности целочисленных переменных позволяет смягчить проблему, хотя полностью ее не устраняет. Например, зададим переменные
byte m=10,n=10,k=10;
Тогда значения m*n, m*k и n*k будут лежать в разрешенном диапазоне -128..127. А вот m*n + m*k из него выйдет. Не говоря уж об m*n*k.
Если мы зададим
short m=10,n=10,k=10;
переполнения не возникнет даже для m*n*k. Однако, при m=n=k=100 значение m*n*k будет равно  , что заметно выходит за пределы разрешенного диапазона –32768..32767. Хотя m*n, m*k и n*k не будут за него выходить (но уже 4*m*n за него выйдет). Использование типа long поможет и в этом случае. Однако уже значения m=n=k=2000 (не такие уж большие!) опять приведут к выходу m*n*k за пределы диапазона. Хотя для m*n выход произойдет только при значениях около 50000.
, что заметно выходит за пределы разрешенного диапазона –32768..32767. Хотя m*n, m*k и n*k не будут за него выходить (но уже 4*m*n за него выйдет). Использование типа long поможет и в этом случае. Однако уже значения m=n=k=2000 (не такие уж большие!) опять приведут к выходу m*n*k за пределы диапазона. Хотя для m*n выход произойдет только при значениях около 50000.
Вычисление факториала с помощью целочисленной арифметики даст удивительные результаты! В таких случаях лучше использовать числа с плавающей точкой. Пример:
byte i=127, j=1, k; k=(byte)(i+j); System.out.println(k);
В результате получим число (-128). Если бы мы попробовали написать
byte i=127,j=1,k; System.out.println(i+j);
то получили бы +128. Напомним, что значения величин типа byte перед проведением сложения преобразуются в значения типа int.