|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Управление ключами
5.3. Соглашение с симметричными ключами
Алиса и Боб могут создать ключ сеанса между собой, не используя KDC. Этот метод создания ключа сеанса называется соглашением с симметричными ключами. Хотя есть несколько способов выполнить этот процесс, здесь рассматриваются только два общих метода ключевого соглашения: Диффи-Хеллмана (Diffie-Hellman) и "станция-к-станции".
Ключевое соглашение
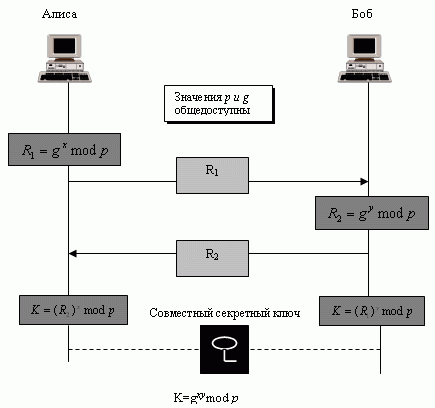
В протоколе Диффи-Хеллмана две стороны создают симметричный ключ сеанса без KDC. Перед установлением симметричного ключа эти две стороны должны выбрать два числа p и g. Первое число, p, является большим простым числом порядка 300 десятичных цифр (1024 бита). Второе число, g, служит генератором порядка p - 1 в группе <Zp*, x >. Эти два числа (группа и генератор) не должны быть конфиденциальными. Их можно передать через Internet. Они могут быть общедоступны. рис. 5.9 показывает процедуру.
Шаги перечислены ниже.
- Алиса выбирает большое случайное число x, такое, что 0 < x < p - 1, и вычисляет R1 = gx mod p.
- Боб выбирает другое большое случайное число y, такое, что 0 < y < p - 1, и вычисляет R2 = gy mod p.
- Алиса передает Бобу R1. Обратите внимание, что Алиса не передает значение x ; она передает только R1.
- Боб передает Алисе R2. Снова обратите внимание, что Боб не передает значение y, он передает только R2.
- Алиса вычисляет K = (R2)x mod p.
- Боб также вычисляет K = (R1)y mod p.
K = (gx mod p)y mod p = (gymod p)x mod p = gxy mod p
Боб вычисляет K = (R1)y mod p = (gx mod p)y mod p = gxy mod p
Алиса вычисляет K = (R2)x mod p = (gy mod p)x mod p = gxy mod p
и получает то же самое значение без Боба, знающего значение x. А Боб получил это значение без Алисы, знающей значение y.
Пример 5.1
Приведем тривиальный пример, чтобы ясно понять процедуру. Наш пример использует маленькие числа, но заметим, что в реальной ситуации применяются очень большие числа. Предположим, что g = 7 и p = 23. Тогда процедура содержит следующие шаги.
- Алиса выбирает x = 3 и вычисляет R1 = 73 mod 23 = 21.
- Боб выбирает y = 6 и вычисляет R2 = 76 mod 23 = 4.
- Алиса передает число 21 Бобу.
- Боб передает число 4 Алисе.
- Алиса вычисляет симметричный ключ K = 43 mod 23 = 18.
- Боб вычисляет симметричный ключ K = 216 mod 23 = 18.
Значение K одно и то же и для Алисы, и для Боба: gx y mod p = 718 = 18 .
Пример 5.2
Давайте возьмем более реальный пример. Мы используем программу, чтобы создать случайное целое число 512 битов (идеально - 1024 бит). Целое число p - число с 159 цифрами. Мы также выбираем g, x и y, как показано ниже:
| p | 764624298563493572182493765955030507476338096726949748923573772860925 235666660755423637423309661180033338106194730130950414738700999178043 6548785807987581 |
|---|---|
| g | 2 |
| x | 557 |
| y | 273 |
Следующая таблица показывает R1, R2 и K.
| R1 | 84492028420 665505216172947491035094143433698520012660862863631067673 619959280828586700802131859290945140217500319973312945836083821943065 966020157955354 |
|---|---|
| R2 | 435262838709200379470747114895581627636389116262115557975123379218566 31001143571S208390040181876486841753831165342691630263421106721508589 6255201288594143 |
| K | 155638000664522290596225827523270765273218046944423678520320400146406 500887936651204257426776608327911017153038674561252213151610976584200 1204086433617740 |
Анализ протокола Диффи-Хеллмана
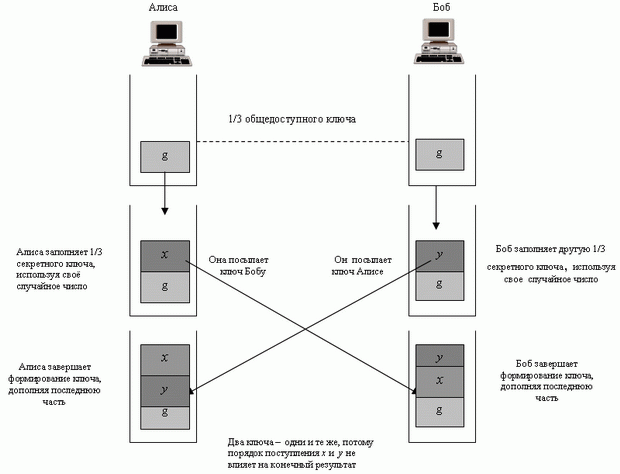
Концепция Диффи-Хеллмана, показанная на рис. 5.10, является простой, но изящной. Мы можем представить ключ засекречивания между Алисой и Бобом - он состоит из трех частей: g, x и y. Первая часть общедоступна. Каждый знает 1/3 ключа - g, общедоступное значение. Другие две части нужно узнать у Алисы и Боба. Каждый из них знает одну часть. Алиса добавляет x как вторую часть для Боба; Боб добавляет y как вторую часть для Алисы. Когда Алиса получает 2/3 полного ключа от Боба, она добавляет последнюю часть, ее y, чтобы завершить ключ. Когда Боб получает ключ от Алисы - законченный на 2/3, он добавляет последнюю часть, свое y, чтобы завершить ключ. Обратите внимание, что хотя ключ Алисы состоит из g, y и x и ключ Боба состоит из g, x и y, эти два ключа - одни и те же, потому что gxy = gyx.
Обратите внимание также, что хотя два ключа те же самые, Алиса не может найти значение y, используемого Бобом, потому что вычисление сделано по модулю p. Алиса получает gy mod p от Боба, но не gy. Для того чтобы знать значения y, Алиса должна использовать дискретный логарифм, который мы обсуждали в предыдущей лекции.
Безопасность протокола
Замена ключа Диффи-Хеллмана восприимчива к двум атакам: атаке дискретного логарифма и атаке посредника (man-in middle)
Атака дискретного логарифма. Безопасность ключевой станции базируется на трудности проблемы дискретного логарифма. Ева может перехватить R1 и R2.
Из R1 = gx mod p и y из R2 = gy mod p она может затем вычислить симметричный ключ: K = gxy mod p. Ключ засекречивания больше не является секретным. Чтобы cделать метод Диффи-Хеллмана защищенным от атаки дискретного логарифма, рекомендуется следующее.
- Простое число p должно быть очень большим (более чем 300 десятичных цифр).
- Простое число p должно быть выбрано так, чтобы p - 1 имел по крайней мере один простой делитель (больше чем 60 десятичных цифр).
- Генератор должен быть выбран из группы <Zp*, x >.
- Боб и Алиса должны уничтожить x и y после того, как они вычислили значение симметричного ключа. Значения x и y должны использоваться только единожды.
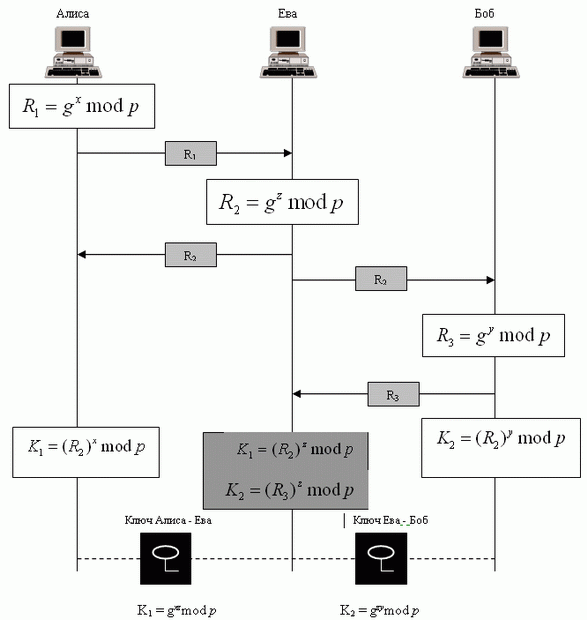
Атака "посредника". Этот протокол имеет другую слабость. Еве не надо находить значения x и y, чтобы напасть на протокол. Она может использовать глупость Алисы и Боба, создающих два ключа: один между Бобом и Алисой и другой между Алисой и Бобом. Рис. 5.11 показывает ситуацию. Может случиться следующее:
- Алиса выбирает x , вычисляет R 1 = gx mod p и передает R1 Бобу.
- Ева, злоумышленник, перехватывает R1. Она выбирает z, вычисляет R 2 = gz mod p и передает R 2 Алисе и Бобу.
- Боб выбирает y, вычисляет R3 = gy mod p, передает R3 Алисе. Ева перехватывает R3, и Алиса никогда не получит это число.
- Алиса и Ева вычисляют K1 = gxz mod p, который становится открытым ключом между Алисой и Евой. Алиса, однако, думает, что это -открытый ключ между ней и Бобом.
- Ева и Боб вычисляют K2 = gzymod p, который становится открытым ключом между Евой и Бобом. Однако Боб думает, что это - открытый ключ между ним Алисой.
Другими словами, создаются два ключа вместо одного: один между Алисой и Евой и один между Евой и Бобом. Когда Алиса посылает данные Бобу, она зашифровывает их ключом K1 (совместный ключ Алисы и Евы). Эти данные могут быть расшифрованы и прочитаны Евой. Ева может передать сообщение Бобу, зашифрованное K2 (совместный ключ между Евой и Бобом); или она может даже изменить сообщение или передать новое сообщение. Боб введен в заблуждение, поскольку уверен, что сообщение пришло от Алисы. Подобный сценарий может случиться и в другом направлении - с Алисой.
Эта ситуация называется " атака посредника ", поскольку Ева находится между партнерами и перехватывает R1, передаваемый Алисой Бобу, и R3, передаваемый Бобом Алисой. Это - атака передачи по цепочке, потому что напоминает короткую линейку добровольцев на пожаре, передающих друг другу ведра с водой, по цепочке от человека человеку.
Следующий метод основан на протоколе Диффи-Хеллмана. Он использует методы установления подлинности, чтобы сорвать эту атаку.
Ключевое соглашение "от станции к станции"
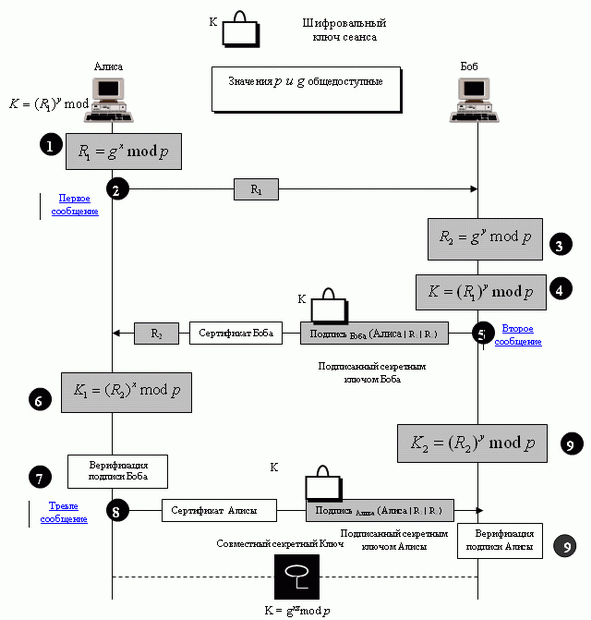
Протокол "от станции к станции" - метод, основанный на методе Диффи-Хеллмана. Он применяет цифровые подписи с сертификатами открытого ключа (см. следующую секцию). Для установки ключа сеанса между Алисой и Бобом используется последовательность, показанная на рис. 5.12.
Имеются следующие шаги:
- После вычисления R1 Алиса передает R1 Бобу (шаги 1 и 2 на рис. 5.12).
- После вычисления R2 и ключа сеанса Боб конкатенирует ID Алисы, R1 И R2. Затем он подписывает результат своим секретным ключом. Боб теперь передает R2, подпись и собственное свидетельство общедоступного ключа Алисе. Подпись зашифрована ключом сеанса (шаги 3, 4 и 5 на рис. 5.12).
- После вычисления ключа сеанса, если подпись Боба проверена, Алиса связывает ID Боба, R1 И R2. Затем она подписывает результат своим собственным секретным ключом и передает это Бобу. Подпись зашифрована ключом сеанса (шаги 6, 7 и 8 на рис. 5.12).
- Если подпись Алисы проверена, Боб сохраняет ключ сеанса (шаг 9 на рис. 5.12).
Безопасность протокола "от станции к станции"
Протокол "от станции к станции" предотвращает атаки "посредника". После R1 Ева не может передать свой собственный R2 Алисе и притворяться, что это идет от Боба, потому что Ева не может подделать секретный ключ Боба и создать подпись - подпись не может быть проверена общедоступным ключом Боба, определенным в свидетельстве. Тем же образом Ева не может подделать секретный ключ Алисы, чтобы подписать третье сообщение, передаваемое Алисой. Сертификату, как мы увидим в следующей секции, можно доверять, потому что он выработан администрацией, которой доверяют.
K=(R1)y mod p