|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Цифровая подпись
Схема цифровой подписи Шнорра
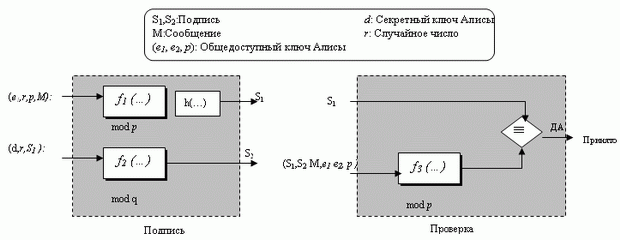
Проблема схемы цифровой подписи Эль-Гамаля - в том, что p должно быть очень большим, чтобы сделать трудной проблему дискретного логарифма Zp*. Рекомендуется длина p по крайней мере 1024 битов. Можно сделать подпись размером 2048 бит. Чтобы уменьшить размер подписи, Шнорр предложил новую схему, основанную на схеме Эль-Гамаля , но с уменьшенным размером подписи. рис. 3.11 дает общую идею схемы цифровой подписи Шнорра.
В процессе подписания две функции создают две подписи; в процессе проверки выход одной функции сравнивается с первой подписью для проверки. рис. 3.11 показывает входы к каждой функции. Важно то, что схема использует два модуля: p и q. Функции 1 и 3 используют p ; функция 2 использует q. Детали входов и функций будут коротко обсуждены далее.
Генерация ключей
Перед подписанием сообщения Алиса должна генерировать ключи и объявить всем общедоступные ключи.
- Алиса выбирает простое число p, которое обычно равно по длине 1024 битам.
- Алиса выбирает другое простое число q, которое имеет тот же самый размер, что и дайджест, созданный функцией криптографического хэширования (в настоящее время 160 битов, но это может измениться в будущем). Простое число q должно делиться на (p - 1). Другими словами, (p - 1) = 0 mod q.
- Алиса выбирает e1, q -тый корень которого был бы равен 1 mod p. Чтобы сделать это, Алиса выбирает примитивный элемент в Zp, e0 (см. "G. Список неприводимых и примитивных полиномов" ) и вычисляет e1 = e0(p-1)/q mod p.
- Алиса выбирает целое число, d, как свой секретный ключ.
- Алиса вычисляет e2 = e1d mod p.
- Общедоступный ключ Алисы - (e1, e2, p, q), ее секретный ключ - (d).
Подписание и проверка
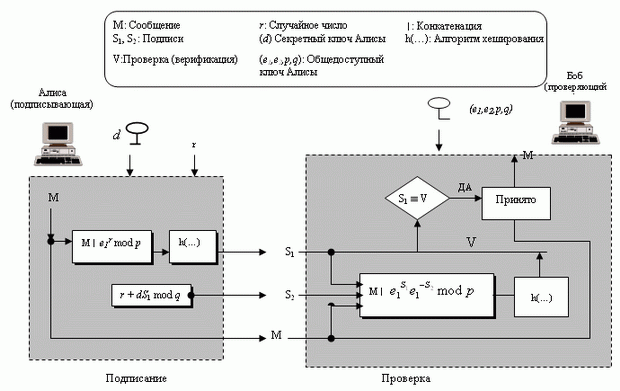
Рисунок 3.12 показывает схему цифровой подписи Шнорра.
Подписание
- Алиса выбирает случайное число r. Обратите внимание, что открытый и секретный ключи могут использоваться для подписи многих сообщений. Но Алиса должна изменять r каждый раз, когда она передает новое сообщение. Обратите внимание также на то, что r должен иметь значение между 1 и q.
- Алиса вычисляет первую подпись S1 = h(M | e1r mod p) . Сообщение присоединяется (конкатенируется) спереди к значению e1r mod p, затем применяется хэш-функция, чтобы создать дайджест. Обратите внимание, что хэш-функция непосредственно не применяется к сообщению, но вместо этого она получается из последовательного соединения М. и e1r mod p.
- Алиса вычисляет вторую подпись S2 = r + d x S1 mod q. Обратите внимание, что эта часть - вычисление S2 - делается в арифметике по модулю q.
- Алиса передает М., S1 и S2.
Верификация (проверка) сообщения. Приемник, например Боб, получает М., S1 и S2.
- Боб вычисляет V = h (М | e1S2 e2-S1 mod p).
- Если S2 конгруэнтно V по модулю p, сообщение принято; иначе оно отклоняется.
Пример 3.4
Вот тривиальный пример. Предположим, что мы выбираем q = 103 и p = 2267. Обратите внимание на то, что p = 22 x q + 1. Мы выбираем e0 = 2, которое является элементом в Z2267*. Тогда (p - 1) / q = 22, так что мы имеем e1 = 222 mod 2267 = 354.
Мы выбираем d = 30, тогда e2 = 35430 mod 2267 = 1206. Секретный ключ Алисы -теперь - (d), ее общедоступный ключ - (e1,e2,p,q).
Алиса хочет передать сообщение М. Она выбирает r = 11 и вычисляет er = 35411 = 630 mod 2267. Предположим, что сообщение - 1000, и конкатенация (последовательное соединение) означает 1000630. Также предположим, что хэширование этого значения дает дайджест h (1000630) = 200. Это означает S1 = 200. Алиса вычисляет S2 = r + d x S1 mod q = 11 + 1026 200 mod 103 = 11 + 24 = 35. Алиса передает сообщение М =1000, S1 = 200 и S2 = 35. Проверку оставляем как упражнение.
Подделка по схеме подписи Шнорра
Похоже, что все атаки на схему Эль-Гамаля могут быть применены к схеме Шнорра. Однако схема Шнорра находится в лучшем положении, потому что S1 = h (М. | e1r(mod p)). Это означает, что хэш-функция применяется к комбинации сообщение и e1r, в которой r является секретным.